Chủ đề bài tập định luật faraday: Bài viết này cung cấp hướng dẫn chi tiết về bài tập định luật Faraday, bao gồm lý thuyết, công thức và các dạng bài tập từ cơ bản đến nâng cao. Đây là nguồn tài liệu hữu ích giúp bạn nắm vững kiến thức vật lý và áp dụng vào các bài tập thực tế.
Mục lục
Bài tập định luật Faraday: Tổng hợp thông tin chi tiết
Định luật Faraday là một trong những nguyên lý quan trọng trong lĩnh vực điện từ học, đóng vai trò quan trọng trong việc giải thích các hiện tượng cảm ứng điện từ và ứng dụng trong nhiều ngành công nghiệp như sản xuất điện năng, chế tạo thiết bị điện tử và các máy móc điện tử khác.
1. Định luật Faraday là gì?
Định luật Faraday phát biểu rằng lực điện động cảm ứng trong một mạch kín bằng độ biến thiên của từ thông qua mạch đó. Điều này có nghĩa là khi từ thông qua một mạch thay đổi theo thời gian, một sức điện động (EMF) sẽ được sinh ra trong mạch đó.
- Công thức cơ bản của định luật Faraday: \[\varepsilon = -\frac{d\Phi_B}{dt}\]
- Trong đó:
- \(\varepsilon\): Suất điện động cảm ứng (V)
- \(\Phi_B\): Từ thông qua mạch (Wb)
- \(t\): Thời gian (s)
2. Ứng dụng của định luật Faraday
Định luật Faraday có nhiều ứng dụng thực tế trong đời sống và công nghiệp:
- Sản xuất điện trong các nhà máy thủy điện, nhiệt điện và điện gió.
- Nguyên lý hoạt động của các máy biến áp, giúp biến đổi điện áp trong hệ thống điện.
- Ứng dụng trong các thiết bị y tế như máy MRI (Cộng hưởng từ).
3. Các dạng bài tập về định luật Faraday
Các bài tập về định luật Faraday thường được phân loại theo các mức độ cơ bản, nâng cao và ứng dụng thực tiễn.
Bài tập cơ bản
- Một bình điện phân đựng dung dịch \(AgNO_3\) có điện trở là \(2,5 \, \Omega\). Catốt của bình điện phân bằng bạc \(Ag\) và hiệu điện thế đặt vào hai điện cực của bình là \(10V\). Tính khối lượng \(m\) của bạc bám vào catốt sau \(16\) phút \(5\) giây. Khối lượng nguyên tử của bạc là \(A=108\) và hóa trị \(n=1\).
Lời giải:
- Đổi \(16\) phút \(5\) giây = \(965\) giây
- Cường độ dòng điện chạy qua bình điện phân là: \[I = \frac{U}{R} = \frac{10}{2,5} = 4 \, A\]
- Khối lượng bạc bám vào catốt sau \(16\) phút \(5\) giây là: \[m = \frac{A \cdot I \cdot t}{n \cdot F} = \frac{108 \cdot 4 \cdot 965}{1 \cdot 96500} = 4,32 \, g\]
Bài tập nâng cao
- Người ta muốn bóc một lớp đồng dày \(d = 10 \, \mu m\) trên một bản đồng diện tích \(S = 1 \, cm^2\) bằng phương pháp điện phân. Cường độ dòng điện là \(0,010 \, A\). Tính thời gian cần thiết để bóc được lớp đồng. Cho biết đồng có khối lượng riêng là \(D = 8900 \, kg/m^3\), khối lượng mol \(64 \, g/mol\) và hóa trị \(2\).
Lời giải:
- Khối lượng đồng phải bóc đi: \[m = D \cdot S \cdot d = 8900 \cdot 1 \cdot 10^{-4} \cdot 10 \cdot 10^{-6} = 8,9 \cdot 10^{-3} \, g\]
- Thời gian cần thiết để bóc được lớp đồng: \[t = \frac{m \cdot F \cdot n}{A \cdot I} = \frac{8,9 \cdot 10^{-3} \cdot 96500 \cdot 2}{64 \cdot 0,010} = 2683 \, s\]
Bài tập ứng dụng thực tiễn
- Cho mạch điện như hình vẽ: Có bộ nguồn \(E = 12 \, V; r = 0,4 \, \Omega\), \(R1 = 9 \, \Omega\), \(R2 = 6 \, \Omega\) và một bình điện phân đựng dung dịch \(CuSO_4\), anôt bằng đồng \(Cu\) và điện trở của bình điện phân \(Rp = 4 \, \Omega\). Tính:
- Cường độ dòng điện qua mạch chính.
- Khối lượng đồng thoát ra ở cực dương trong \(16\) phút \(5\) giây.
Gợi ý: Sử dụng công thức định luật Faraday và các công thức liên quan để giải quyết bài toán.
4. Kết luận
Định luật Faraday và các bài tập liên quan đóng vai trò quan trọng trong việc hiểu và ứng dụng kiến thức vật lý vào thực tế. Việc nắm vững định luật này không chỉ giúp học sinh, sinh viên vượt qua các kỳ thi mà còn cung cấp nền tảng vững chắc cho các ứng dụng công nghệ sau này.

.png)
1. Tổng quan về Định luật Faraday
Định luật Faraday là một trong những nguyên lý quan trọng nhất trong lĩnh vực điện từ học, được phát hiện bởi nhà khoa học Michael Faraday vào năm 1831. Định luật này miêu tả mối quan hệ giữa sự thay đổi của từ thông và suất điện động cảm ứng trong mạch điện, đặt nền tảng cho nhiều ứng dụng trong kỹ thuật và công nghệ hiện đại.
Cụ thể, định luật Faraday bao gồm hai phần chính:
- Định luật Faraday về cảm ứng điện từ: Định luật này phát biểu rằng khi từ thông qua một mạch điện kín thay đổi theo thời gian, một suất điện động (EMF) sẽ được cảm ứng trong mạch đó. Công thức toán học của định luật này là:
\[
\varepsilon = -\frac{d\Phi_B}{dt}
\]
Trong đó:
- \(\varepsilon\) là suất điện động cảm ứng (V).
- \(\Phi_B\) là từ thông qua mạch (Wb).
- \(t\) là thời gian (s).
- Định luật Faraday về điện phân: Định luật này mô tả mối quan hệ giữa khối lượng chất được giải phóng tại điện cực và điện lượng truyền qua dung dịch trong quá trình điện phân. Định luật này có hai phần:
- Định luật thứ nhất: Khối lượng chất sinh ra tại điện cực tỉ lệ thuận với điện lượng truyền qua dung dịch:
\[
m = k \cdot q
\]
Trong đó:
- \(m\) là khối lượng chất sinh ra (g).
- \(q\) là điện lượng (Coulomb, C).
- \(k\) là đương lượng điện hóa của chất (g/C).
- Định luật thứ hai: Đương lượng điện hóa của một chất tỉ lệ thuận với đương lượng hóa học của chất đó và nghịch với hóa trị của nó:
\[
k = \frac{A}{nF}
\]
Trong đó:
- \(A\) là khối lượng mol của chất (g/mol).
- \(n\) là hóa trị của chất.
- \(F\) là hằng số Faraday (\(F \approx 96485\) C/mol).
- Định luật thứ nhất: Khối lượng chất sinh ra tại điện cực tỉ lệ thuận với điện lượng truyền qua dung dịch:
\[
m = k \cdot q
\]
Trong đó:
Nhờ có các định luật này, con người đã phát triển được nhiều công nghệ quan trọng như máy phát điện, máy biến áp và các thiết bị điện tử hiện đại. Đồng thời, định luật Faraday cũng đặt nền móng cho các nguyên lý và ứng dụng trong lĩnh vực điện hóa học, đặc biệt là trong công nghệ mạ điện và tinh chế kim loại.
2. Ứng dụng của Định luật Faraday trong thực tiễn
Định luật Faraday không chỉ là một nguyên lý lý thuyết mà còn có nhiều ứng dụng thực tế trong đời sống và công nghiệp. Các ứng dụng này đóng vai trò quan trọng trong việc phát triển công nghệ và cải thiện hiệu suất trong nhiều lĩnh vực.
- Sản xuất điện năng: Định luật Faraday là cơ sở cho nguyên lý hoạt động của các máy phát điện. Khi cuộn dây dẫn quay trong từ trường hoặc từ trường thay đổi xung quanh cuộn dây, một suất điện động được cảm ứng, tạo ra dòng điện. Các nhà máy thủy điện, nhiệt điện và điện gió đều sử dụng nguyên lý này để biến đổi năng lượng cơ học thành điện năng.
- Công nghệ máy biến áp: Định luật Faraday cũng được ứng dụng trong thiết kế và vận hành máy biến áp, thiết bị giúp biến đổi điện áp của dòng điện xoay chiều (AC) mà không thay đổi tần số. Nhờ đó, việc truyền tải điện năng trên các khoảng cách xa trở nên hiệu quả hơn, giảm thiểu tổn thất điện năng.
- Thiết bị y tế: Một trong những ứng dụng quan trọng của định luật Faraday trong y tế là máy chụp cộng hưởng từ (MRI). Nguyên lý này được sử dụng để tạo ra hình ảnh chi tiết của các cơ quan bên trong cơ thể mà không cần phải phẫu thuật, giúp chẩn đoán bệnh một cách chính xác và an toàn.
- Công nghiệp luyện kim và điện phân: Định luật Faraday về điện phân là cơ sở cho nhiều quy trình công nghiệp như mạ điện, tinh chế kim loại và sản xuất hóa chất. Ví dụ, trong quá trình mạ điện, một lớp kim loại mỏng được bám lên bề mặt vật liệu khác để tạo ra một lớp phủ bảo vệ hoặc trang trí.
- Cảm biến điện từ: Nhiều loại cảm biến trong công nghiệp và dân dụng, như cảm biến tốc độ hoặc cảm biến vị trí, hoạt động dựa trên nguyên lý của định luật Faraday. Chúng biến đổi thông tin về vị trí, tốc độ hoặc lực thành tín hiệu điện, giúp điều khiển tự động các hệ thống.
Những ứng dụng của định luật Faraday không chỉ thể hiện sự sâu sắc của nguyên lý vật lý này mà còn chứng minh tính thực tiễn và tầm quan trọng của nó trong việc thúc đẩy tiến bộ khoa học và công nghệ.

3. Các dạng bài tập về Định luật Faraday
Bài tập về Định luật Faraday có thể phân thành nhiều dạng khác nhau, từ cơ bản đến nâng cao, nhằm giúp học sinh nắm vững nguyên lý và áp dụng vào các tình huống thực tế. Dưới đây là các dạng bài tập phổ biến thường gặp trong các đề thi và bài kiểm tra.
- Bài tập tính suất điện động cảm ứng:
Dạng bài tập này yêu cầu học sinh tính toán suất điện động cảm ứng \(\varepsilon\) sinh ra trong một mạch kín khi từ thông \(\Phi_B\) thay đổi theo thời gian. Công thức áp dụng là:
\[ \varepsilon = -\frac{d\Phi_B}{dt} \]Ví dụ: Một cuộn dây được đặt trong từ trường có cường độ từ trường thay đổi. Yêu cầu tính suất điện động cảm ứng xuất hiện trong cuộn dây sau một khoảng thời gian nhất định.
- Bài tập về từ thông:
Bài tập dạng này thường yêu cầu tính toán hoặc xác định sự thay đổi của từ thông \(\Phi_B\) qua một diện tích nhất định khi từ trường hoặc góc hợp bởi đường sức từ và diện tích thay đổi. Công thức sử dụng là:
\[ \Phi_B = B \cdot A \cdot \cos(\theta) \]Ví dụ: Tính từ thông qua một khung dây có diện tích \(A\) khi cường độ từ trường \(B\) và góc \(\theta\) thay đổi.
- Bài tập về điện phân:
Dạng bài tập này liên quan đến việc tính toán khối lượng chất sinh ra tại các điện cực trong quá trình điện phân, dựa trên định luật Faraday về điện phân. Công thức thường dùng là:
\[ m = k \cdot q = \frac{A \cdot I \cdot t}{n \cdot F} \]Trong đó:
- \(m\) là khối lượng chất sinh ra (g).
- \(k\) là đương lượng điện hóa (g/C).
- \(q\) là điện lượng (C).
- \(A\) là khối lượng mol của chất (g/mol).
- \(I\) là cường độ dòng điện (A).
- \(t\) là thời gian (s).
- \(n\) là hóa trị của chất.
- \(F\) là hằng số Faraday.
Ví dụ: Tính khối lượng đồng được giải phóng tại catốt trong một quá trình điện phân dung dịch CuSO₄ với dòng điện \(I = 2A\) trong thời gian \(t = 10\) phút.
- Bài tập kết hợp nhiều yếu tố:
Đây là dạng bài tập phức tạp hơn, yêu cầu kết hợp nhiều khái niệm và công thức trong định luật Faraday, như từ thông, suất điện động cảm ứng và điện phân, để giải quyết vấn đề.
Ví dụ: Một khung dây dẫn được di chuyển trong từ trường đều. Tính suất điện động cảm ứng sinh ra và khối lượng kim loại lắng đọng trong một quá trình điện phân dựa trên dòng điện cảm ứng sinh ra.
Việc giải các dạng bài tập trên không chỉ giúp học sinh củng cố kiến thức về định luật Faraday mà còn phát triển kỹ năng tư duy và ứng dụng kiến thức vào thực tiễn.
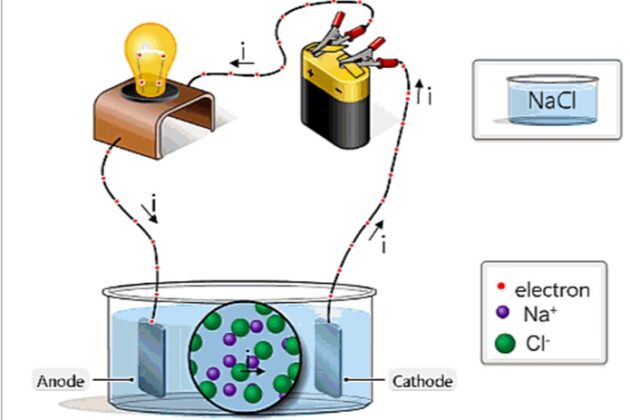
4. Phân tích chuyên sâu các bài tập tiêu biểu
Phân tích các bài tập tiêu biểu về Định luật Faraday là một phần quan trọng trong việc nắm vững và áp dụng kiến thức lý thuyết vào thực tiễn. Dưới đây là phân tích chi tiết từng bước của một số bài tập tiêu biểu, giúp bạn hiểu rõ hơn về phương pháp giải và cách áp dụng công thức.
- Bài tập về suất điện động cảm ứng trong mạch kín:
Ví dụ: Một khung dây dẫn hình chữ nhật có diện tích \(A = 0,2 \, \text{m}^2\) được đặt trong từ trường đều \(B = 0,5 \, \text{T}\). Khung dây quay đều với tốc độ góc \(\omega = 2 \, \text{rad/s}\). Tính suất điện động cảm ứng \(\varepsilon\) sinh ra trong khung dây.
Phân tích:
- Bước 1: Xác định từ thông qua khung dây tại thời điểm bất kỳ: \[ \Phi_B(t) = B \cdot A \cdot \cos(\omega t) \]
- Bước 2: Sử dụng định luật Faraday để tính suất điện động cảm ứng: \[ \varepsilon = -\frac{d\Phi_B(t)}{dt} = B \cdot A \cdot \omega \cdot \sin(\omega t) \]
- Bước 3: Thay giá trị cụ thể vào để tính toán: \[ \varepsilon = 0,5 \cdot 0,2 \cdot 2 \cdot \sin(2t) = 0,2 \cdot \sin(2t) \, \text{V} \]
Suất điện động cảm ứng trong khung dây sẽ dao động với biên độ \(0,2 \, \text{V}\).
- Bài tập về điện phân:
Ví dụ: Một dung dịch CuSO₄ được điện phân bằng dòng điện \(I = 1,5 \, \text{A}\) trong thời gian \(t = 30 \, \text{phút}\). Tính khối lượng đồng \(Cu\) thu được tại catốt. Biết khối lượng mol của đồng là \(63,5 \, \text{g/mol}\) và hóa trị của đồng là 2.
Phân tích:
- Bước 1: Tính điện lượng truyền qua dung dịch: \[ q = I \cdot t = 1,5 \times 1800 = 2700 \, \text{C} \]
- Bước 2: Áp dụng định luật Faraday thứ hai để tính khối lượng đồng sinh ra: \[ m = \frac{A \cdot q}{n \cdot F} = \frac{63,5 \times 2700}{2 \times 96485} \approx 0,89 \, \text{g} \]
Khối lượng đồng thu được tại catốt là khoảng \(0,89 \, \text{g}\).
- Bài tập về biến áp:
Ví dụ: Một máy biến áp lý tưởng có cuộn sơ cấp với \(N_1 = 1000\) vòng và cuộn thứ cấp với \(N_2 = 200\) vòng. Điện áp đầu vào là \(U_1 = 220 \, \text{V}\). Tính điện áp đầu ra \(U_2\).
Phân tích:
- Bước 1: Áp dụng công thức biến áp: \[ \frac{U_2}{U_1} = \frac{N_2}{N_1} \]
- Bước 2: Tính toán điện áp đầu ra: \[ U_2 = U_1 \cdot \frac{N_2}{N_1} = 220 \cdot \frac{200}{1000} = 44 \, \text{V} \]
Điện áp đầu ra của máy biến áp là \(44 \, \text{V}\).
Qua các bài tập trên, bạn sẽ hiểu rõ hơn cách áp dụng định luật Faraday vào các tình huống thực tế, từ đó củng cố kiến thức và phát triển kỹ năng giải bài tập vật lý.

5. Tài liệu tham khảo và nguồn học liệu
Để nắm vững Định luật Faraday và áp dụng vào giải các bài tập một cách hiệu quả, việc tham khảo các tài liệu học tập và nguồn học liệu chất lượng là rất quan trọng. Dưới đây là một số tài liệu và nguồn học liệu bạn có thể sử dụng:
- Sách giáo khoa Vật Lý:
Hầu hết các sách giáo khoa Vật Lý lớp 11 đều có chương trình chi tiết về Định luật Faraday. Các ví dụ và bài tập trong sách giáo khoa là nguồn học liệu chính thống và đáng tin cậy.
- Giáo trình điện từ học:
Các giáo trình về điện từ học ở bậc đại học cũng cung cấp kiến thức sâu rộng về Định luật Faraday. Giáo trình này không chỉ giúp bạn hiểu rõ lý thuyết mà còn đưa ra các bài tập phức tạp hơn để rèn luyện kỹ năng giải toán.
- Bài giảng online:
Các bài giảng trực tuyến trên YouTube và các nền tảng học tập như Coursera, EdX cũng là những nguồn học liệu phong phú. Các giáo viên giảng dạy thường giải thích chi tiết và minh họa bằng các ví dụ cụ thể, giúp bạn dễ dàng hiểu và áp dụng kiến thức.
- Website giáo dục:
Các website chuyên về giáo dục như Hocmai, Violet, hoặc Khan Academy có nhiều bài viết và video hướng dẫn chi tiết về Định luật Faraday. Đây là những tài liệu bổ sung hữu ích cho việc tự học.
- Tài liệu ôn thi:
Các tài liệu ôn thi, sách luyện thi đại học cũng cung cấp nhiều bài tập và đề thi mẫu về Định luật Faraday. Những tài liệu này giúp bạn rèn luyện khả năng làm bài và chuẩn bị tốt cho các kỳ thi.
- Diễn đàn học tập:
Các diễn đàn như Diendan.hocmai.vn, Vozforums, hoặc các nhóm học tập trên Facebook là nơi bạn có thể thảo luận, chia sẻ và giải đáp các thắc mắc liên quan đến Định luật Faraday cùng với các học sinh và giáo viên khác.
Việc kết hợp các tài liệu trên sẽ giúp bạn có cái nhìn toàn diện và sâu sắc hơn về Định luật Faraday, từ đó nâng cao hiệu quả học tập và giải quyết tốt các bài tập liên quan.

.jpg)




















