Cách Tính Nguyên Tử Khối Và Các Công Thức Cụ Thể

Nguyên tử khối là khối lượng của một nguyên tử tính theo đơn vị khối lượng nguyên tử (amu), thường bằng 1/12 khối lượng của một nguyên tử carbon-12. Việc tính toán nguyên tử khối trung bình của một nguyên tố hóa học cần xem xét các đồng vị của nguyên tố đó và tỷ lệ phần trăm của mỗi đồng vị.

1. Công Thức Tính Nguyên Tử Khối Trung Bình

Để tính nguyên tử khối trung bình của một nguyên tố có nhiều đồng vị, ta sử dụng công thức sau:

\[
\text{Nguyên tử khối trung bình} = \frac{{x_1 \cdot M_1 + x_2 \cdot M_2 + \ldots + x_n \cdot M_n}}{{100}}
\]

Trong đó:

• \(x_1, x_2, \ldots, x_n\) là tỷ lệ phần trăm của mỗi đồng vị.
• \(M_1, M_2, \ldots, M_n\) là khối lượng của các đồng vị tương ứng.

2. Các Bước Tính Nguyên Tử Khối

1. Xác định các đồng vị của nguyên tố cần tính.
2. Tìm khối lượng của mỗi đồng vị.
3. Xác định tỷ lệ phần trăm của mỗi đồng vị.
4. Áp dụng công thức để tính nguyên tử khối trung bình.

3. Ví Dụ Cụ Thể

Giả sử nguyên tố \(X\) có hai đồng vị với thông tin như sau:

• Đồng vị \(X_1\) có khối lượng \(M_1 = 35\) amu, tỷ lệ phần trăm \(x_1 = 75\%\).
• Đồng vị \(X_2\) có khối lượng \(M_2 = 37\) amu, tỷ lệ phần trăm \(x_2 = 25\%\).

Nguyên tử khối trung bình của \(X\) được tính như sau:

\[
\text{Nguyên tử khối trung bình} = \frac{{75 \cdot 35 + 25 \cdot 37}}{{100}} = 35.5 \, \text{amu}
\]

4. Ứng Dụng Trong Thực Tiễn

Việc tính nguyên tử khối trung bình không chỉ giúp xác định khối lượng của nguyên tử mà còn hỗ trợ trong nhiều lĩnh vực khoa học như hóa học, vật liệu, và sinh học.

5. Lưu Ý Khi Tính Toán

• Khối lượng electron rất nhỏ so với proton và neutron nên thường không tính đến trong tính toán nguyên tử khối.
• Khi tính toán, cần chú ý đến độ chính xác của số liệu để đảm bảo kết quả đúng.

Nguyên tử khối là khối lượng của một nguyên tử, được tính bằng đơn vị khối lượng nguyên tử (đvC), còn được gọi là đơn vị carbon. Đơn vị này bằng 1/12 khối lượng của một nguyên tử carbon-12.

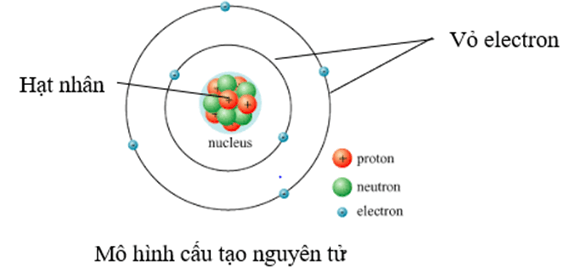
Khối lượng nguyên tử bao gồm tổng khối lượng của các proton, neutron và electron có trong nguyên tử đó. Tuy nhiên, do khối lượng của electron rất nhỏ (khoảng 0,00055u) so với khối lượng của proton và neutron (khoảng 1u mỗi hạt), khối lượng nguyên tử thường được coi là tổng khối lượng của các proton và neutron trong hạt nhân.

Công thức tính khối lượng nguyên tử như sau:

Trong đó:

• \(m_{\text{NT}}\) là khối lượng nguyên tử
• \(m_{p}\) là khối lượng của proton
• \(m_{n}\) là khối lượng của neutron

Khối lượng nguyên tử có thể khác nhau tùy theo số lượng neutron trong hạt nhân, dẫn đến sự tồn tại của các đồng vị khác nhau của cùng một nguyên tố. Nguyên tử khối trung bình của một nguyên tố được tính dựa trên khối lượng và tỉ lệ phần trăm số nguyên tử của các đồng vị của nguyên tố đó.

Công thức tính nguyên tử khối trung bình của một nguyên tố có nhiều đồng vị như sau:

Trong đó:

• a, b, c,... là số nguyên tử (hoặc tỉ lệ phần trăm số nguyên tử) của mỗi đồng vị.
• A, B, C,... là nguyên tử khối của mỗi đồng vị.

Nguyên tử khối trung bình là giá trị trung bình của khối lượng nguyên tử các đồng vị của một nguyên tố, có tính đến tỉ lệ phần trăm số nguyên tử của từng đồng vị trong hỗn hợp. Công thức tính nguyên tử khối trung bình được biểu diễn như sau:

• Giả sử một nguyên tố có hai đồng vị \(A\) và \(B\), với nguyên tử khối tương ứng là \(A\) và \(B\).
• Tỉ lệ phần trăm số nguyên tử của đồng vị \(A\) là \(a\%\) và của đồng vị \(B\) là \(b\%\).

Công thức tính nguyên tử khối trung bình:

\[
\bar{A} = \frac{A \times a + B \times b}{100}
\]

Trong đó:

• \(\bar{A}\): Nguyên tử khối trung bình của nguyên tố.
• \(A\): Nguyên tử khối của đồng vị thứ nhất.
• \(B\): Nguyên tử khối của đồng vị thứ hai.
• \(a\%\): Tỉ lệ phần trăm số nguyên tử của đồng vị \(A\).
• \(b\%\): Tỉ lệ phần trăm số nguyên tử của đồng vị \(B\).

Ví dụ, nếu nguyên tố X có hai đồng vị với nguyên tử khối là 35 và 37, và tỉ lệ phần trăm số nguyên tử của chúng lần lượt là 75% và 25%, nguyên tử khối trung bình của X sẽ được tính như sau:

\[
\bar{X} = \frac{35 \times 75 + 37 \times 25}{100} = 35.5 \, \text{(đvC)}
\]

Trong hóa học, đồng vị là các biến thể của một nguyên tố có cùng số proton nhưng khác nhau về số neutron, dẫn đến sự khác biệt về khối lượng nguyên tử. Mỗi đồng vị có khối lượng riêng và tỉ lệ phần trăm tự nhiên trong môi trường.

Để tính nguyên tử khối trung bình của một nguyên tố có nhiều đồng vị, ta sử dụng công thức:

Trong đó:

• A₁, A₂, ... A_n là khối lượng của các đồng vị.
• \%\_1, \%\_2, ... \%\_n là phần trăm tỷ lệ của các đồng vị tương ứng.

Ví dụ, để tính nguyên tử khối của Clo, một nguyên tố có hai đồng vị là \(^{35}Cl\) và \(^{37}Cl\) với tỉ lệ phần trăm lần lượt là 75,77% và 24,23%, ta áp dụng công thức như sau:

Nhờ vào việc tính toán này, chúng ta có thể xác định được nguyên tử khối trung bình của một nguyên tố dựa trên tỷ lệ phần trăm tự nhiên của các đồng vị của nó.

Để hiểu rõ hơn về cách tính nguyên tử khối, chúng ta cùng đi qua một ví dụ minh họa cụ thể. Giả sử chúng ta cần tính nguyên tử khối trung bình của một nguyên tố X có hai đồng vị: đồng vị X1 có khối lượng 63 amu chiếm 75% và đồng vị X2 có khối lượng 65 amu chiếm 25%.

Công thức tính nguyên tử khối trung bình được áp dụng như sau:

Thay các giá trị vào công thức:

Thực hiện các phép tính:

Như vậy, nguyên tử khối trung bình của nguyên tố X là 63.50 amu. Điều này có nghĩa là khi tính đến sự tồn tại của các đồng vị với tỷ lệ phần trăm khác nhau, khối lượng trung bình của một nguyên tử X là 63.50 đơn vị khối lượng nguyên tử (amu).

Việc tính toán này rất quan trọng trong hóa học, đặc biệt là khi làm việc với các nguyên tố có nhiều đồng vị tự nhiên. Nó giúp chúng ta hiểu rõ hơn về khối lượng thực sự của các nguyên tố khi chúng tồn tại trong tự nhiên và ảnh hưởng đến các tính chất vật lý cũng như hóa học của chúng.

Nguyên tử khối là một khái niệm cơ bản trong hóa học, đóng vai trò quan trọng trong nhiều lĩnh vực khoa học và công nghiệp. Dưới đây là một số ứng dụng của nguyên tử khối:

• Xác định tính chất vật lý và hóa học của các nguyên tố: Nguyên tử khối giúp xác định các tính chất như điểm sôi, điểm nóng chảy, độ dẫn điện, và khả năng phản ứng hóa học của các nguyên tố. Ví dụ, nguyên tử khối càng lớn thì nguyên tố đó thường có điểm sôi và điểm nóng chảy cao hơn.
• Tính toán khối lượng mol: Nguyên tử khối của một nguyên tố là cơ sở để tính toán khối lượng mol của nó, một yếu tố quan trọng trong việc cân bằng phản ứng hóa học. Ví dụ, để tính khối lượng của một mol khí oxy (\(O_2\)), ta có thể sử dụng nguyên tử khối của oxy là 16u để tính toán: \[M(O_2) = 2 \times 16 = 32 \, \text{g/mol}\].
• Sản xuất và phân tích vật liệu: Trong công nghiệp, nguyên tử khối được sử dụng để thiết kế các vật liệu mới với các tính chất mong muốn. Điều này đặc biệt quan trọng trong ngành luyện kim, sản xuất hợp kim và các vật liệu bán dẫn.
• Phân tích phổ khối: Nguyên tử khối là một thông số quan trọng trong phổ khối, một kỹ thuật được sử dụng để xác định thành phần của một chất và cấu trúc phân tử của nó. Ví dụ, khi phân tích thành phần của một hợp chất hữu cơ, phổ khối có thể giúp xác định chính xác các nguyên tố và nhóm chức có mặt trong phân tử.
• Nghiên cứu dược phẩm và y học: Trong y học, nguyên tử khối được sử dụng để thiết kế thuốc và phân tích sự chuyển hóa của chúng trong cơ thể. Điều này giúp xác định liều lượng chính xác và giảm thiểu tác dụng phụ không mong muốn.

Như vậy, nguyên tử khối không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tiễn, góp phần quan trọng trong nhiều ngành khoa học và công nghiệp.

Khi tính toán nguyên tử khối, có một số lưu ý quan trọng mà bạn cần phải nhớ để đảm bảo độ chính xác và tính toán đúng cách. Dưới đây là các bước và lưu ý cụ thể:

• Xác định nguyên tử khối trung bình:

  Nguyên tử khối của một nguyên tố thường là trung bình của các đồng vị khác nhau của nguyên tố đó, được tính dựa trên tỷ lệ phần trăm số nguyên tử của mỗi đồng vị. Công thức tính toán nguyên tử khối trung bình được biểu diễn như sau:

  \[\text{Ā} = \frac{a \times A + b \times B + c \times C + \ldots}{100}\]

  Trong đó:

  • \(A\), \(B\), \(C\) là nguyên tử khối của các đồng vị.
  • \(a\), \(b\), \(c\) là tỷ lệ phần trăm số nguyên tử của từng đồng vị tương ứng.
• Sử dụng đơn vị khối lượng nguyên tử (đvC):

  Đơn vị khối lượng nguyên tử (đvC) là 1/12 khối lượng của nguyên tử Carbon-12 (C₁₂), tương đương với:

  \[1 \text{ đvC} = 1.6605 \times 10^{-24} \text{g}\]

  Lưu ý rằng khối lượng của các hạt electron thường rất nhỏ và có thể bỏ qua trong nhiều phép tính.

• Tính khối lượng thực của nguyên tử:

  Khi đã xác định nguyên tử khối, khối lượng thực của một nguyên tử có thể tính bằng cách nhân nguyên tử khối với đơn vị khối lượng nguyên tử:

  \[m_A = \text{Nguyên tử khối} \times 1.6605 \times 10^{-24} \text{g}\]

• Chọn số liệu từ bảng nguyên tử khối:

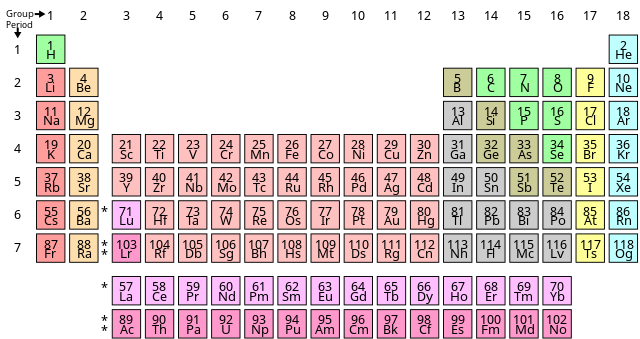
  Khi tính toán nguyên tử khối, bạn cần tra cứu giá trị từ bảng nguyên tử khối tiêu chuẩn và nhớ rằng các nguyên tố có thể có nhiều hóa trị khác nhau, vì vậy hãy chắc chắn sử dụng giá trị đúng với hóa trị đang tính toán.

Qua các bước trên, việc tính toán nguyên tử khối sẽ trở nên đơn giản và chính xác hơn, giúp bạn hiểu rõ hơn về cấu trúc và khối lượng của các nguyên tố hóa học.

Qua quá trình nghiên cứu và tìm hiểu về cách tính nguyên tử khối, chúng ta đã rút ra nhiều kết luận quan trọng về tính chất và ứng dụng của nguyên tử khối trong khoa học và đời sống.

• Nguyên tử khối là đại lượng đo khối lượng của một nguyên tử, chủ yếu tập trung ở khối lượng của các proton và neutron trong hạt nhân, với đơn vị thường sử dụng là đơn vị carbon (\(\text{đvC}\)).
• Việc tính toán nguyên tử khối trung bình của một nguyên tố dựa trên khối lượng và tỷ lệ phần trăm của các đồng vị tự nhiên là phương pháp chính xác và được áp dụng rộng rãi. Công thức tính nguyên tử khối trung bình là: \[ M_{tb} = \frac{{a_1 \cdot M_1 + a_2 \cdot M_2 + \cdots + a_n \cdot M_n}}{100} \]
• Nguyên tử khối không chỉ giúp xác định tính chất của các nguyên tố mà còn đóng vai trò quan trọng trong nhiều lĩnh vực như y học, công nghệ và bảo vệ môi trường. Khối lượng nguyên tử giúp chúng ta hiểu rõ hơn về cấu trúc vi mô của vật chất và cách các nguyên tử tương tác với nhau trong các phản ứng hóa học.

Như vậy, nguyên tử khối không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tiễn, giúp chúng ta giải quyết các vấn đề trong nhiều lĩnh vực khác nhau. Sự hiểu biết về cách tính và ứng dụng của nguyên tử khối là nền tảng quan trọng cho việc nghiên cứu và phát triển khoa học kỹ thuật trong tương lai.