Chủ đề công thức tính nguyên tử khối trung bình: Bài viết này sẽ cung cấp cho bạn cách tính nguyên tử khối trung bình một cách chi tiết, từ công thức cơ bản đến các ví dụ minh họa cụ thể. Cùng khám phá các khái niệm quan trọng trong hóa học và áp dụng vào thực tế để nâng cao kiến thức của bạn.
Mục lục
Công Thức Tính Nguyên Tử Khối Trung Bình
Nguyên tử khối trung bình của một nguyên tố là khối lượng trung bình của các đồng vị của nguyên tố đó, được tính theo phần trăm số lượng của từng đồng vị. Đây là một khái niệm quan trọng trong hóa học, giúp xác định khối lượng của nguyên tử dựa trên sự tồn tại tự nhiên của các đồng vị.
1. Công Thức Tính
Nguyên tử khối trung bình của một nguyên tố có công thức tính như sau:
\[
A_{tb} = \frac{X_1 \times A_1 + X_2 \times A_2 + \dots + X_n \times A_n}{X_1 + X_2 + \dots + X_n}
\]
Trong đó:
- \(A_{tb}\): Nguyên tử khối trung bình
- \(X_1, X_2, \dots, X_n\): Phần trăm số lượng của các đồng vị
- \(A_1, A_2, \dots, A_n\): Nguyên tử khối của các đồng vị tương ứng
2. Ví Dụ Minh Họa
Xét nguyên tố Cl có hai đồng vị là \(^{35}\text{Cl}\) và \(^{37}\text{Cl}\) với tỷ lệ phần trăm tương ứng là 75,77% và 24,23%. Nguyên tử khối của Cl được tính như sau:
\[
A_{tb} = \frac{75.77 \times 35 + 24.23 \times 37}{100} = 35.485
\]
Như vậy, nguyên tử khối trung bình của Cl là 35.485.
3. Lưu Ý Khi Tính Toán
- Đảm bảo rằng phần trăm số lượng của các đồng vị tổng cộng phải là 100%.
- Phải sử dụng đơn vị khối lượng nguyên tử (amu) khi tính toán.
- Kết quả nên được làm tròn đến số thập phân hợp lý tùy vào yêu cầu bài toán.
4. Ứng Dụng Thực Tiễn
Công thức này không chỉ giúp học sinh hiểu rõ hơn về bản chất của nguyên tố mà còn giúp trong việc xác định phân tử khối của các hợp chất khi đã biết nguyên tử khối trung bình của các nguyên tố thành phần.

.png)
1. Định Nghĩa Nguyên Tử Khối Trung Bình
Nguyên tử khối trung bình của một nguyên tố là giá trị trung bình của khối lượng các đồng vị của nguyên tố đó, có tính đến độ phong phú tự nhiên của mỗi đồng vị. Để hiểu rõ hơn, chúng ta cần xét đến khái niệm đồng vị và độ phong phú tự nhiên.
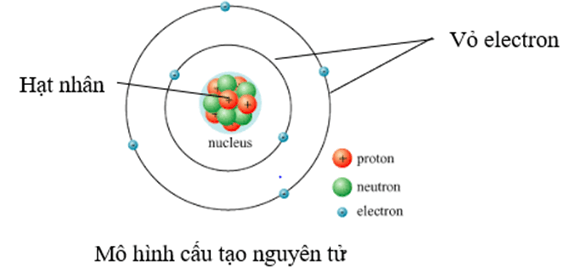
Một nguyên tố có thể tồn tại dưới nhiều dạng đồng vị khác nhau, mỗi đồng vị có số lượng nơtron khác nhau trong hạt nhân, dẫn đến khối lượng nguyên tử khác nhau. Độ phong phú tự nhiên là phần trăm của mỗi đồng vị trong tự nhiên. Khi tính toán nguyên tử khối trung bình, chúng ta cần xem xét cả khối lượng của từng đồng vị và độ phong phú của chúng.
Công thức tính nguyên tử khối trung bình như sau:
\[ \overline{M} = f_1 \times m_1 + f_2 \times m_2 + \dots + f_n \times m_n \]
Trong đó:
- \(\overline{M}\): Nguyên tử khối trung bình
- \(f_n\): Độ phong phú tự nhiên của đồng vị thứ \(n\)
- \(m_n\): Khối lượng nguyên tử của đồng vị thứ \(n\)
Ví dụ, nguyên tố Clo có hai đồng vị bền là \(^{35}Cl\) và \(^{37}Cl\). Độ phong phú của chúng lần lượt là 75,78% và 24,22%. Khối lượng nguyên tử trung bình của Clo được tính bằng cách:
\[ \overline{M} = \frac{(34,96885 \times 75,78) + (36,96590 \times 24,22)}{100} = 35,45 \, \text{amu} \]
Như vậy, nguyên tử khối trung bình là đại lượng đại diện cho khối lượng trung bình của các nguyên tử của một nguyên tố có xét đến sự tồn tại của các đồng vị.
2. Công Thức Tính Nguyên Tử Khối Trung Bình
Công thức tính nguyên tử khối trung bình cho một nguyên tố được xác định dựa trên khối lượng của các đồng vị và độ phong phú tự nhiên của chúng. Công thức cụ thể như sau:
\[ \overline{M} = \frac{\sum_{i=1}^{n} (f_i \times m_i)}{100} \]
Trong đó:
- \(\overline{M}\): Nguyên tử khối trung bình của nguyên tố.
- \(f_i\): Độ phong phú phần trăm của đồng vị thứ \(i\) trong tự nhiên.
- \(m_i\): Khối lượng nguyên tử của đồng vị thứ \(i\).
- \(n\): Số lượng các đồng vị của nguyên tố.
Để tính toán, chúng ta thực hiện theo các bước sau:
- Xác định các đồng vị của nguyên tố và độ phong phú tự nhiên tương ứng của chúng.
- Tính tích của khối lượng từng đồng vị với độ phong phú tương ứng.
- Tổng hợp tất cả các tích lại.
- Chia kết quả cho 100 để thu được nguyên tử khối trung bình.
Ví dụ, với nguyên tố Clo có hai đồng vị chính là \(^{35}Cl\) và \(^{37}Cl\) với độ phong phú lần lượt là 75,78% và 24,22%, công thức tính sẽ là:
\[ \overline{M} = \frac{(34,96885 \times 75,78) + (36,96590 \times 24,22)}{100} = 35,45 \, \text{amu} \]
Như vậy, giá trị \(35,45 \, \text{amu}\) là nguyên tử khối trung bình của Clo, được tính dựa trên độ phong phú và khối lượng của hai đồng vị.

3. Ví Dụ Minh Họa Cách Tính
Để minh họa cách tính nguyên tử khối trung bình, chúng ta sẽ sử dụng nguyên tố Magiê (Mg) làm ví dụ. Magiê có ba đồng vị chính với các khối lượng và độ phong phú như sau:
| Đồng vị | Khối lượng (amu) | Độ phong phú (%) |
| \(^{24}Mg\) | 23,98504 | 78,99 |
| \(^{25}Mg\) | 24,98584 | 10,00 |
| \(^{26}Mg\) | 25,98259 | 11,01 |
Áp dụng công thức tính nguyên tử khối trung bình:
\[
\overline{M}_{Mg} = \frac{(23,98504 \times 78,99) + (24,98584 \times 10,00) + (25,98259 \times 11,01)}{100}
\]
Tính toán từng bước:
- Tính tích của từng đồng vị với độ phong phú tương ứng:
- \(23,98504 \times 78,99 = 1895,633 \, \text{amu}\)
- \(24,98584 \times 10,00 = 249,8584 \, \text{amu}\)
- \(25,98259 \times 11,01 = 286,0466 \, \text{amu}\)
- Tổng hợp các tích lại:
- \(1895,633 + 249,8584 + 286,0466 = 2431,538 \, \text{amu}\)
- Chia kết quả cho 100 để thu được nguyên tử khối trung bình:
- \( \overline{M}_{Mg} = \frac{2431,538}{100} = 24,31538 \, \text{amu} \)
Vậy, nguyên tử khối trung bình của Magiê là \(24,32 \, \text{amu}\) (làm tròn đến hai chữ số thập phân).

4. Các Lỗi Thường Gặp Khi Tính Toán
Khi tính toán nguyên tử khối trung bình, có một số lỗi phổ biến mà học sinh thường mắc phải. Những lỗi này có thể dẫn đến kết quả sai lệch, làm ảnh hưởng đến độ chính xác của bài toán. Dưới đây là một số lỗi thường gặp và cách tránh chúng:
- Không nhân độ phong phú theo phần trăm:
Đôi khi, học sinh quên chuyển đổi độ phong phú từ phần trăm thành giá trị thập phân trước khi nhân với khối lượng đồng vị. Điều này dẫn đến việc giá trị trung bình bị lệch so với thực tế. Để tránh lỗi này, luôn đảm bảo chuyển đổi độ phong phú bằng cách chia cho 100 trước khi nhân.
- Nhầm lẫn giữa các đồng vị:
Trong quá trình tính toán, việc nhầm lẫn giữa các đồng vị hoặc gán sai khối lượng cho đồng vị có thể dẫn đến kết quả sai. Hãy chắc chắn rằng bạn đã ghi nhận đúng khối lượng và độ phong phú của từng đồng vị.
- Sai sót khi tính tổng:
Một số học sinh có thể tính tổng sai do lỗi cộng trừ hoặc không cẩn thận khi tính toán trên giấy nháp. Để tránh điều này, hãy kiểm tra lại phép tính của mình, đặc biệt là khi cộng các tích của khối lượng và độ phong phú.
- Không làm tròn đúng cách:
Nguyên tử khối trung bình thường cần được làm tròn đến một số chữ số thập phân nhất định. Việc làm tròn không đúng cách có thể dẫn đến sai sót nhỏ nhưng ảnh hưởng lớn trong các bài toán tiếp theo. Hãy làm tròn đúng theo yêu cầu của đề bài.
Bằng cách cẩn thận và chú ý đến các chi tiết trên, bạn có thể tránh được những lỗi thường gặp khi tính toán nguyên tử khối trung bình, từ đó đảm bảo kết quả chính xác hơn.

5. Tài Liệu Tham Khảo Và Bài Tập Thực Hành
Để hiểu rõ hơn về cách tính nguyên tử khối trung bình và áp dụng vào thực tế, bạn cần tham khảo các tài liệu và làm các bài tập thực hành. Dưới đây là một số tài liệu và bài tập giúp bạn củng cố kiến thức và nâng cao kỹ năng:
- Giáo trình Hóa học lớp 10:
Nội dung chương trình Hóa học lớp 10 cung cấp kiến thức cơ bản về nguyên tử khối trung bình, bao gồm định nghĩa, công thức và cách áp dụng vào bài tập. Đây là tài liệu học tập chính thống giúp bạn nắm vững nền tảng lý thuyết.
- Bài tập thực hành:
- Bài tập 1: Tính nguyên tử khối trung bình của một nguyên tố có hai đồng vị với khối lượng và độ phong phú lần lượt là \(X_1\) và \(X_2\).
- Bài tập 2: Xác định nguyên tử khối trung bình khi biết ba đồng vị của nguyên tố với độ phong phú khác nhau.
- Bài tập 3: So sánh và phân tích kết quả tính toán nguyên tử khối trung bình trong các trường hợp sai số nhỏ.
- Video hướng dẫn:
Các video hướng dẫn trên YouTube sẽ giúp bạn hình dung cụ thể hơn về quy trình tính toán và tránh được những lỗi thường gặp. Bạn có thể tìm kiếm các từ khóa như "hướng dẫn tính nguyên tử khối trung bình" để tìm các video phù hợp.
- Website học trực tuyến:
Các trang web như Hocmai.vn, Tuyensinh247.com cung cấp nhiều bài giảng và bài tập luyện tập để bạn thực hành và kiểm tra kiến thức của mình về nguyên tử khối trung bình.
Qua việc tham khảo các tài liệu và thực hành bài tập, bạn sẽ nắm vững kiến thức và kỹ năng tính toán nguyên tử khối trung bình một cách chính xác và hiệu quả.