Chủ đề 3 điện tích q giống hệt nhau: Bài viết "3 điện tích q giống hệt nhau: Khám phá bài toán và ứng dụng thực tiễn" sẽ giúp bạn hiểu rõ hơn về khái niệm, cách tính toán lực tương tác và điện trường, cũng như ứng dụng của chúng trong thực tế. Hãy cùng tìm hiểu những bài toán thú vị và cách giải quyết chúng một cách chi tiết và dễ hiểu.
Mục lục
Tổng hợp thông tin về chủ đề "3 điện tích q giống hệt nhau"
Chủ đề "3 điện tích q giống hệt nhau" thường xuất hiện trong các bài giảng và bài tập Vật lý, đặc biệt là trong phần về điện trường và lực tương tác giữa các điện tích. Dưới đây là tổng hợp chi tiết về nội dung này:
1. Khái niệm cơ bản
Một hệ ba điện tích q giống hệt nhau thường được xem xét trong các bài toán Vật lý liên quan đến lực tương tác và điện trường. Các điện tích này thường được đặt tại các đỉnh của một tam giác đều có cạnh a. Việc tính toán lực tương tác và cường độ điện trường tại tâm của tam giác là những bài toán cơ bản và thường gặp.
2. Độ lớn cường độ điện trường tại tâm tam giác đều
Đối với một tam giác đều có ba điện tích q giống hệt nhau đặt tại các đỉnh, tổng hợp lực tại tâm của tam giác thường bằng 0 do các lực do mỗi điện tích gây ra triệt tiêu lẫn nhau. Cụ thể:
- Cường độ điện trường do mỗi điện tích q tại tâm M của tam giác là \( E = k \frac{q}{r^2} \), với \( r \) là khoảng cách từ đỉnh tam giác đến tâm.
- Do sự đối xứng, các vectơ cường độ điện trường tổng hợp tại tâm M có xu hướng triệt tiêu lẫn nhau, dẫn đến \( E_{\text{tổng hợp}} = 0 \).
3. Ứng dụng trong bài tập
Chủ đề này thường xuất hiện trong các bài tập về tính toán điện trường, lực tương tác và năng lượng của hệ điện tích. Một ví dụ điển hình là bài toán xác định cường độ điện trường tại tâm tam giác đều khi biết ba điện tích q đặt tại các đỉnh.
4. Mở rộng và liên quan
Các khái niệm liên quan đến hệ điện tích này còn được mở rộng sang các bài toán phức tạp hơn, bao gồm cả việc xét lực tương tác khi điện tích thứ tư được thêm vào hệ, hoặc khi các điện tích q không giống hệt nhau.
5. Bài tập minh họa
- Ba điện tích q giống nhau đặt tại các đỉnh A, B, C của một tam giác đều cạnh a. Xác định cường độ điện trường tại tâm tam giác.
- Xét một hệ gồm ba điện tích dương q đặt tại ba đỉnh của một tam giác đều, tìm độ lớn lực tác dụng lên một điện tích khác đặt tại tâm của tam giác.
Kết luận
Chủ đề về "3 điện tích q giống hệt nhau" không chỉ là một bài toán lý thú trong Vật lý mà còn giúp học sinh hiểu rõ hơn về các khái niệm cơ bản như lực tương tác, điện trường và nguyên lý đối xứng trong tự nhiên. Những bài toán này cũng tạo nền tảng cho việc nghiên cứu sâu hơn trong lĩnh vực Điện học và các ứng dụng thực tiễn trong đời sống.
.png)
1. Khái niệm cơ bản về ba điện tích q
Trong Vật lý, khái niệm về ba điện tích q giống hệt nhau thường xuất hiện trong các bài toán liên quan đến điện trường và lực tương tác giữa các điện tích. Ba điện tích này thường được xem xét trong một hệ thống lý tưởng, nơi các điện tích q được đặt cố định tại các đỉnh của một tam giác đều có cạnh là a.
Để hiểu rõ hơn về ba điện tích q, chúng ta cần nắm bắt những yếu tố cơ bản sau:
- Điện tích điểm: Điện tích q được coi là một điện tích điểm, tức là điện tích tập trung tại một điểm trong không gian, không chiếm diện tích và không có kích thước.
- Hệ ba điện tích: Khi ba điện tích q được đặt tại các đỉnh của tam giác đều, chúng tạo ra một hệ thống cân bằng về mặt hình học, với các lực tác dụng lên nhau theo nguyên tắc đối xứng.
- Điện trường tại tâm: Tại tâm của tam giác đều, điện trường do ba điện tích q gây ra có đặc tính đặc biệt. Do tính đối xứng của hệ, tổng hợp lực điện tại tâm thường triệt tiêu, làm cho điện trường tại tâm bằng không.
- Lực tương tác giữa các điện tích: Mỗi cặp điện tích trong hệ này tạo ra lực đẩy hoặc lực hút theo Coulomb, với độ lớn phụ thuộc vào khoảng cách giữa chúng và độ lớn của điện tích q.
Kết luận, ba điện tích q giống hệt nhau trong một tam giác đều là một mô hình lý tưởng để nghiên cứu các nguyên lý cơ bản của điện trường và lực tương tác trong Vật lý. Bằng cách phân tích hệ này, ta có thể hiểu sâu hơn về cách thức hoạt động của các lực trong tự nhiên cũng như các ứng dụng thực tiễn liên quan.
2. Lực tương tác giữa ba điện tích q
Lực tương tác giữa ba điện tích q là một trong những khái niệm quan trọng trong Vật lý, đặc biệt là khi nghiên cứu về điện trường và lực Coulomb. Khi ba điện tích q giống hệt nhau được đặt tại các đỉnh của một tam giác đều, các lực tương tác giữa chúng có thể được phân tích như sau:
- Lực Coulomb: Lực tương tác giữa hai điện tích điểm q theo định luật Coulomb được xác định bằng công thức:
\[
F = k \cdot \frac{|q_1 \cdot q_2|}{r^2}
\]
Trong đó:
- \(F\) là lực tương tác giữa hai điện tích q.
- \(k\) là hằng số Coulomb (\(k \approx 9 \times 10^9 \, \text{Nm}^2/\text{C}^2\)).
- \(q_1\) và \(q_2\) là độ lớn của các điện tích (ở đây \(q_1 = q_2 = q\)).
- \(r\) là khoảng cách giữa hai điện tích.
- Tổng hợp lực tại mỗi đỉnh: Khi xét lực tương tác giữa ba điện tích q trong một tam giác đều, mỗi điện tích chịu tác dụng của hai lực từ hai điện tích còn lại. Các lực này có phương nằm trên đường nối giữa các đỉnh và được tổng hợp theo quy tắc hình bình hành.
- Do tính đối xứng của tam giác đều, hai lực tác dụng lên một điện tích tại một đỉnh sẽ có cùng độ lớn và hợp với nhau một góc \(60^\circ\).
- Tổng hợp lực tại mỗi đỉnh có thể được tính bằng công thức: \[ F_{\text{tổng hợp}} = F \times \sqrt{3} \] với \(F\) là lực Coulomb giữa hai điện tích q.
- Tính chất của hệ ba điện tích q: Trong hệ ba điện tích q đặt tại các đỉnh của tam giác đều, các lực tương tác giữa chúng có đặc tính đối xứng, dẫn đến sự triệt tiêu lẫn nhau của các thành phần lực tại tâm tam giác. Điều này giúp hệ giữ được trạng thái cân bằng nếu không có ngoại lực tác động.
Như vậy, lực tương tác giữa ba điện tích q trong một tam giác đều là một bài toán cơ bản nhưng đầy thú vị, giúp chúng ta hiểu rõ hơn về các quy luật của điện học và cách các lực tương tác với nhau trong một hệ đối xứng.

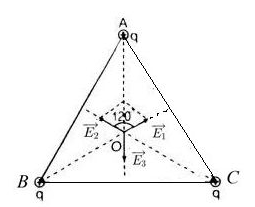
3. Điện trường tổng hợp tại tâm tam giác
Khi ba điện tích q giống hệt nhau được đặt tại các đỉnh của một tam giác đều, điện trường tổng hợp tại tâm tam giác là một khái niệm quan trọng trong Vật lý. Điện trường tại một điểm là tổng hợp các vectơ điện trường do các điện tích gây ra. Dưới đây là cách tính toán và phân tích điện trường tổng hợp tại tâm tam giác đều:
- Điện trường do một điện tích q gây ra: Điện trường \( E \) tại một điểm cách điện tích q một khoảng r được xác định bằng công thức:
\[
E = k \cdot \frac{q}{r^2}
\]
Trong đó:
- \(k\) là hằng số điện môi, \(k \approx 9 \times 10^9 \, \text{Nm}^2/\text{C}^2\).
- \(q\) là độ lớn của điện tích.
- \(r\) là khoảng cách từ điện tích đến điểm cần xét (ở đây là tâm tam giác).
- Điện trường tổng hợp tại tâm tam giác: Do ba điện tích q giống nhau và cách đều tâm tam giác, mỗi điện tích gây ra một điện trường tại tâm tam giác với cùng độ lớn nhưng khác hướng.
- Các vectơ điện trường này hợp thành một hệ thống đối xứng.
- Theo nguyên tắc tổng hợp vectơ, do các vectơ điện trường có cùng độ lớn và tạo thành các góc \(120^\circ\) với nhau, chúng sẽ triệt tiêu lẫn nhau, dẫn đến điện trường tổng hợp tại tâm tam giác bằng 0.
- Kết luận: Điện trường tổng hợp tại tâm của tam giác đều với ba điện tích q giống hệt nhau bằng 0. Điều này xuất phát từ sự đối xứng hoàn hảo của hệ thống, làm cho các thành phần điện trường tại tâm triệt tiêu lẫn nhau.
Như vậy, điện trường tổng hợp tại tâm tam giác đều là một minh họa rõ ràng cho tính đối xứng trong hệ điện tích, giúp người học hiểu rõ hơn về cách các lực và điện trường tương tác và triệt tiêu lẫn nhau trong các hệ thống đối xứng.

XEM THÊM:
4. Ứng dụng và bài tập liên quan
Các bài toán liên quan đến ba điện tích q giống hệt nhau không chỉ là các bài tập lý thuyết trong Vật lý mà còn có nhiều ứng dụng thực tiễn quan trọng. Dưới đây là một số ứng dụng và bài tập liên quan giúp người học hiểu rõ hơn về khái niệm này.
- Ứng dụng trong thiết kế hệ thống điện: Việc nghiên cứu lực tương tác giữa các điện tích có thể được áp dụng vào việc thiết kế các hệ thống điện tử, cảm biến, và các thiết bị điện tử khác. Hiểu rõ về cách các điện tích tương tác giúp kỹ sư có thể tối ưu hóa khoảng cách và vị trí các thành phần trong mạch điện để đảm bảo hiệu suất cao nhất.
- Ứng dụng trong vật lý thiên văn: Trong thiên văn học, các nguyên lý về lực tương tác giữa các điện tích có thể được áp dụng để nghiên cứu sự tương tác giữa các hạt trong vũ trụ, bao gồm các hạt mang điện như proton, electron trong các tinh vân hoặc môi trường liên sao.
- Bài tập tính toán lực tương tác: Một bài tập phổ biến là tính toán lực tổng hợp tác dụng lên một điện tích khi biết vị trí của các điện tích còn lại trong hệ ba điện tích q. Ví dụ:
- Cho ba điện tích q được đặt tại các đỉnh của một tam giác đều cạnh a. Hãy tính lực tác dụng lên mỗi điện tích.
- Hãy tính điện trường tại một điểm nằm trên đường trung trực của một cạnh tam giác đều chứa các điện tích q.
- Bài tập mở rộng: Ngoài việc giải các bài toán cơ bản về ba điện tích q, người học còn có thể mở rộng bài toán với các biến thể khác như thay đổi vị trí điện tích, thêm điện tích thứ tư vào hệ thống, hoặc nghiên cứu trường hợp không đều về khoảng cách giữa các điện tích. Các bài tập này giúp củng cố và mở rộng kiến thức về điện trường và lực tương tác.
Những ứng dụng và bài tập trên không chỉ giúp người học nắm vững kiến thức về điện tích mà còn phát triển tư duy logic và kỹ năng giải quyết vấn đề, từ đó áp dụng vào các lĩnh vực thực tiễn khác nhau.

5. Mở rộng kiến thức về điện tích
Sau khi đã nắm vững các khái niệm cơ bản về ba điện tích q giống hệt nhau, chúng ta có thể mở rộng kiến thức về điện tích qua các khía cạnh phức tạp và đa dạng hơn. Dưới đây là một số chủ đề mở rộng giúp bạn hiểu sâu hơn về điện tích và các hiện tượng liên quan.
- Điện tích và thuyết điện từ: Khám phá mối quan hệ giữa điện tích và từ trường, cũng như cách các điện tích chuyển động tạo ra từ trường theo định luật Ampère và Faraday. Những khái niệm này là cơ sở cho các ứng dụng như động cơ điện và máy phát điện.
- Tương tác giữa nhiều điện tích: Khi số lượng điện tích trong một hệ tăng lên, việc tính toán lực tương tác và điện trường trở nên phức tạp hơn. Nghiên cứu các phương pháp tính toán lực tương tác trong hệ nhiều điện tích, bao gồm phương pháp tổng hợp vectơ và nguyên lý chồng chập.
- Điện tích trong môi trường vật chất: Tìm hiểu về cách điện tích phân bố trong các vật liệu khác nhau như chất cách điện, chất dẫn điện, và chất bán dẫn. Khái niệm về điện môi, độ phân cực và điện dung cũng là những kiến thức quan trọng khi nghiên cứu điện tích trong các môi trường này.
- Ứng dụng thực tiễn của điện tích: Nghiên cứu các ứng dụng của điện tích trong đời sống hằng ngày như trong các thiết bị lưu trữ năng lượng (pin, tụ điện), công nghệ cảm biến, và điện tử học. Khám phá cách điện tích được sử dụng trong y học, công nghiệp và công nghệ tiên tiến.
- Các hiện tượng đặc biệt liên quan đến điện tích: Nghiên cứu các hiện tượng đặc biệt như sự phóng điện, hiệu ứng quang điện, và hiện tượng siêu dẫn, nơi các điện tích có những hành vi bất thường hoặc đặc biệt trong các điều kiện nhất định.
Việc mở rộng kiến thức về điện tích không chỉ giúp bạn hiểu rõ hơn về các nguyên lý cơ bản mà còn cung cấp nền tảng vững chắc để khám phá những ứng dụng và hiện tượng phức tạp hơn trong Vật lý và công nghệ.
6. Tổng kết và lưu ý quan trọng
Qua các phân tích và tính toán ở trên, chúng ta có thể rút ra một số kết luận quan trọng liên quan đến hệ ba điện tích q giống hệt nhau trong tam giác đều:
- Tính đối xứng của hệ: Do tính chất đối xứng của tam giác đều, lực tương tác giữa các điện tích q sẽ cân bằng tại tâm tam giác, làm cho tổng hợp lực tại tâm bằng không.
- Cường độ điện trường tại tâm: Cường độ điện trường tại tâm tam giác là kết quả của sự cộng hưởng từ các vectơ điện trường tạo ra bởi từng điện tích tại các đỉnh. Độ lớn của cường độ này được tính dựa trên khoảng cách từ tâm đến các đỉnh của tam giác.
- Lưu ý về lực tương tác: Khi các điện tích có cùng dấu, lực tương tác giữa chúng là lực đẩy. Nếu dấu của một trong các điện tích thay đổi, lực tương tác sẽ thay đổi từ lực đẩy sang lực hút, ảnh hưởng đến sự cân bằng của hệ.
- Ứng dụng thực tế: Hệ ba điện tích trong tam giác đều là mô hình cơ bản giúp hiểu rõ hơn về điện trường tổng hợp và các hiện tượng tương tác điện trong không gian ba chiều, có thể ứng dụng trong thiết kế các mạch điện và phân tích các hệ thống tương tự trong vật lý.
Lưu ý khi giải bài tập:
- Khi tính toán, cần đảm bảo sử dụng đúng đơn vị và kiểm tra lại các giá trị khoảng cách giữa các điện tích.
- Các bài toán phức tạp hơn có thể yêu cầu tính toán bằng các phương pháp vector hoặc sử dụng các phần mềm hỗ trợ để đạt độ chính xác cao.
- Nên vẽ hình minh họa để dễ hình dung và giảm thiểu sai sót trong quá trình tính toán.