Vật Lý 10 Bài 25: Động Năng Thế Năng - Khám Phá Chi Tiết Và Bài Tập Ứng Dụng

Bài học này giới thiệu và phân tích các khái niệm cơ bản về động năng và thế năng, hai dạng năng lượng quan trọng trong vật lý. Cùng với đó là các công thức và ứng dụng thực tế trong việc tính toán và giải bài tập.

1. Động năng

Động năng là năng lượng mà một vật có được nhờ vào chuyển động của nó. Động năng của một vật khối lượng \( m \) đang chuyển động với vận tốc \( v \) được tính bằng công thức:

\[
W_d = \frac{1}{2} m v^2
\]

Trong đó:

• \( W_d \): Động năng (đơn vị: Jun - J)
• \( m \): Khối lượng của vật (đơn vị: Kilogram - kg)
• \( v \): Vận tốc của vật (đơn vị: Mét trên giây - m/s)

2. Thế năng

Thế năng trọng trường là năng lượng mà một vật có được do vị trí của nó trong trường trọng lực. Thế năng của một vật có khối lượng \( m \) đặt ở độ cao \( h \) so với mặt đất được tính theo công thức:

\[
W_t = m g h
\]

Trong đó:

• \( W_t \): Thế năng trọng trường (đơn vị: Jun - J)
• \( g \): Gia tốc trọng trường (thường lấy \( g = 9,8 \, \text{m/s}^2 \))
• \( h \): Độ cao của vật so với mốc thế năng (đơn vị: Mét - m)

3. Mối quan hệ giữa công và năng lượng

Công của lực tác dụng lên một vật có thể làm thay đổi động năng của vật đó. Đối với lực không đổi tác dụng lên vật trong khoảng thời gian nhất định, công được tính bằng:

\[
A = \Delta W_d = W_{d2} - W_{d1} = \frac{1}{2} m (v_2^2 - v_1^2)
\]

Ngoài ra, công của lực nâng một vật trong trường trọng lực cũng bằng thế năng của vật đó tại độ cao tương ứng:

\[
W_t = A = m g h
\]

4. Bài tập minh họa

Dưới đây là một số bài tập minh họa liên quan đến động năng và thế năng:

• Bài tập 1: Một ô tô khối lượng 2 tấn chuyển động từ điểm A đến điểm B trên mặt phẳng ngang, sau đó tiếp tục chuyển động lên một mặt phẳng nghiêng BC. Tính động năng của ô tô tại điểm B và xác định liệu ô tô có đủ năng lượng để vượt qua đỉnh C hay không.
• Bài tập 2: Một máy đóng cọc có đầu búa nặng 0,5 tấn, được nâng lên độ cao 10 m. Tính thế năng của đầu búa ở độ cao này.

Những bài tập này giúp củng cố kiến thức về động năng, thế năng và cách tính toán trong các tình huống thực tế.

Trong bài học Vật Lý 10, bài 25, chúng ta sẽ tìm hiểu về hai khái niệm quan trọng trong cơ học là động năng và thế năng. Đây là hai dạng năng lượng quan trọng và có ứng dụng rộng rãi trong nhiều hiện tượng tự nhiên và kỹ thuật.

• Động năng (Kinetic Energy): Động năng là năng lượng mà một vật có được nhờ vào chuyển động của nó. Động năng phụ thuộc vào khối lượng và vận tốc của vật.

Động năng của một vật được tính bằng công thức:

\[
K = \frac{1}{2}mv^2
\]

Trong đó:

• \(K\) là động năng (đơn vị: Joule)
• \(m\) là khối lượng của vật (đơn vị: Kilogram)
• \(v\) là vận tốc của vật (đơn vị: m/s)

• Thế năng (Potential Energy): Thế năng là năng lượng mà một vật có được do vị trí của nó trong trường lực, chẳng hạn như trọng lực hoặc lực đàn hồi.

Thế năng của một vật nằm trong trường trọng lực được tính bằng công thức:

\[
U = mgh
\]

Trong đó:

• \(U\) là thế năng trọng trường (đơn vị: Joule)
• \(m\) là khối lượng của vật (đơn vị: Kilogram)
• \(g\) là gia tốc trọng trường (đơn vị: m/s²)
• \(h\) là độ cao của vật so với mốc thế năng (đơn vị: Meter)

Thế năng đàn hồi của một lò xo được tính bằng công thức:

\[
U = \frac{1}{2}kx^2
\]

Trong đó:

• \(U\) là thế năng đàn hồi (đơn vị: Joule)
• \(k\) là độ cứng của lò xo (đơn vị: N/m)
• \(x\) là độ biến dạng của lò xo (đơn vị: Meter)

Cả động năng và thế năng đều là những khái niệm quan trọng giúp giải thích và dự đoán chuyển động cũng như tương tác của các vật thể trong thế giới tự nhiên.

Trong phần này, chúng ta sẽ tìm hiểu về các định luật và nguyên lý liên quan đến động năng và thế năng, bao gồm các định luật bảo toàn năng lượng và các nguyên lý liên hệ giữa động năng và thế năng.

1. Định luật bảo toàn động năng

Định luật bảo toàn động năng phát biểu rằng: “Trong hệ kín và không chịu tác động của ngoại lực, tổng động năng của hệ không đổi.” Trong trường hợp này, công của các lực ngoại sinh sẽ làm thay đổi động năng của vật thể. Công thức cơ bản:

\( \Delta W_{đ} = A \), với:

• \( W_{đ} \): Động năng của vật.
• \( A \): Công của lực tác dụng.

2. Định luật bảo toàn thế năng

Thế năng là dạng năng lượng mà vật thể có được do vị trí hoặc cấu trúc của nó trong trường hấp dẫn. Định luật bảo toàn thế năng phát biểu rằng: “Khi chỉ có lực hấp dẫn tác dụng lên một vật, tổng thế năng của vật không đổi.” Công thức tính thế năng trọng trường là:

\( W_{t} = m \cdot g \cdot h \), với:

• \( W_{t} \): Thế năng trọng trường (J).
• \( m \): Khối lượng của vật (kg).
• \( g \): Gia tốc trọng trường (m/s²).
• \( h \): Độ cao của vật so với mốc tính (m).

3. Nguyên lý động năng - thế năng

Nguyên lý này chỉ ra rằng trong một hệ cô lập, khi vật di chuyển, năng lượng sẽ chuyển đổi qua lại giữa động năng và thế năng. Khi thế năng giảm, động năng sẽ tăng và ngược lại. Mối quan hệ này được mô tả qua phương trình:

\( \frac{1}{2}mv_{1}^{2} + mgh_{1} = \frac{1}{2}mv_{2}^{2} + mgh_{2} \)

Biểu thức trên cho thấy tổng động năng và thế năng của vật tại hai thời điểm khác nhau là bằng nhau nếu không có tác động của các lực khác.

4. Ứng dụng của định luật bảo toàn năng lượng

Định luật bảo toàn năng lượng có nhiều ứng dụng trong đời sống và kỹ thuật, như trong các hệ thống cơ học, máy móc và thiết bị vận chuyển. Ví dụ, khi một chiếc cần cẩu nâng một vật lên, năng lượng được chuyển từ thế năng của vật tại độ cao cao hơn thành công cơ học để thực hiện công việc.

Trong phần này, chúng ta sẽ tìm hiểu về các dạng bài tập liên quan đến động năng và thế năng cùng với các phương pháp giải chi tiết. Các bài tập này được chia thành nhiều dạng, từ cơ bản đến nâng cao, giúp học sinh nắm vững kiến thức và áp dụng linh hoạt vào thực tế.

1. Bài tập tính động năng

• Bài tập 1: Một vật có khối lượng 2 kg đang chuyển động với vận tốc 3 m/s. Tính động năng của vật.

Hướng dẫn giải: Áp dụng công thức tính động năng \( W_{\text{động năng}} = \frac{1}{2}mv^2 \), thay các giá trị vào ta có:

\( W_{\text{động năng}} = \frac{1}{2} \times 2 \times 3^2 = 9 \text{ J} \)

• Bài tập 2: Một mũi tên nặng 48 g đang chuyển động với tốc độ 10 m/s. Tìm động năng của mũi tên.

Hướng dẫn giải: Chuyển đổi khối lượng sang kg (0.048 kg) và áp dụng công thức tương tự:

\( W_{\text{động năng}} = \frac{1}{2} \times 0.048 \times 10^2 = 2.4 \text{ J} \)

2. Bài tập tính thế năng

• Bài tập 1: Một vật có khối lượng 3 kg được nâng lên độ cao 2 m so với mặt đất. Tính thế năng trọng trường của vật (lấy \( g = 9.8 \, \text{m/s}^2 \)).

Hướng dẫn giải: Áp dụng công thức tính thế năng \( W_{\text{thế năng}} = mgh \), ta có:

\( W_{\text{thế năng}} = 3 \times 9.8 \times 2 = 58.8 \text{ J} \)

• Bài tập 2: Một máy đóng cọc nâng búa lên độ cao 5 m. Tính thế năng của búa nếu khối lượng của nó là 150 kg.

Hướng dẫn giải: Áp dụng công thức tương tự:

\( W_{\text{thế năng}} = 150 \times 9.8 \times 5 = 7350 \text{ J} \)

3. Bài tập vận dụng định luật bảo toàn năng lượng

• Bài tập 1: Thả một quả bóng từ độ cao h xuống sàn nhà. Động năng của quả bóng được chuyển hóa thành những dạng năng lượng nào ngay khi quả bóng chạm sàn?

Hướng dẫn giải: Động năng chuyển hóa thành thế năng (làm quả bóng nảy lên), nhiệt năng (làm nóng quả bóng) và năng lượng âm thanh (phát ra tiếng).

• Bài tập 2: Một vật có khối lượng 10 kg chuyển động trên mặt phẳng nằm ngang với vận tốc 5 m/s, sau đó dừng lại do ma sát. Tính công của lực ma sát.

Hướng dẫn giải: Tính động năng ban đầu và áp dụng công thức công của lực ma sát.

4. Hướng dẫn chi tiết cách giải các bài tập

Để giải các bài tập về động năng và thế năng hiệu quả, các bước sau đây có thể áp dụng:

1. Xác định dạng bài tập (động năng, thế năng, bảo toàn năng lượng).
2. Viết ra các công thức cần sử dụng.
3. Thay các giá trị đã cho vào công thức và tính toán cẩn thận.
4. Kiểm tra đơn vị và tính hợp lý của kết quả.

Những bước trên sẽ giúp bạn tiếp cận và giải quyết các bài tập từ đơn giản đến phức tạp một cách dễ dàng và chính xác.

Động năng và thế năng không chỉ là những khái niệm lý thuyết mà còn có rất nhiều ứng dụng thực tế trong đời sống hàng ngày, công nghệ và kỹ thuật. Dưới đây là một số ứng dụng điển hình:

1. Động năng trong đời sống

• Giao thông: Động năng được sử dụng trong các phương tiện như ô tô, xe máy và tàu hỏa. Khi các phương tiện này di chuyển, chúng có động năng và nó phụ thuộc vào khối lượng và vận tốc của chúng. Việc phanh hay tăng tốc đều liên quan đến sự thay đổi động năng.
• Thể thao: Trong các môn thể thao như bóng đá, bóng rổ, động năng của bóng tăng lên khi vận tốc của nó tăng, giúp các cầu thủ điều chỉnh được lực sút hoặc ném bóng.

2. Thế năng trong các hiện tượng tự nhiên

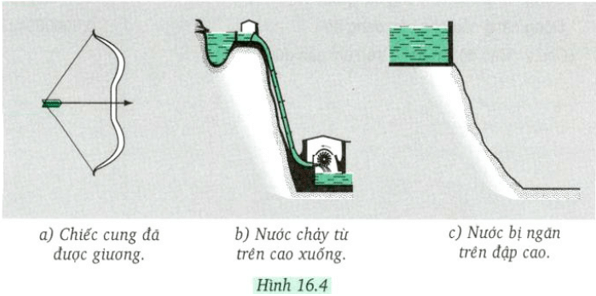
• Thác nước và nhà máy thủy điện: Thế năng của nước ở độ cao được chuyển hóa thành động năng khi nước chảy xuống, từ đó tạo ra điện năng thông qua các tua-bin.
• Con lắc và chuyển động dao động: Trong một con lắc đơn, thế năng cực đại khi con lắc ở vị trí cao nhất và chuyển hóa hoàn toàn thành động năng khi nó đạt vận tốc lớn nhất ở vị trí thấp nhất.

3. Ứng dụng trong công nghệ và kỹ thuật

• Công nghệ lưu trữ năng lượng: Pin và hệ thống lưu trữ năng lượng dùng cơ chế biến đổi qua lại giữa động năng và thế năng để duy trì năng lượng ở trạng thái cần thiết.
• Cơ chế hoạt động của máy móc: Các máy móc như máy ép thủy lực, máy nén khí sử dụng sự biến đổi giữa thế năng và động năng để thực hiện công việc với hiệu suất cao.

Qua bài học này, các bạn đã nắm được những kiến thức cơ bản về động năng và thế năng, cũng như mối quan hệ giữa chúng. Dưới đây là phần tổng kết và các điểm cần lưu ý khi ôn tập.

1. Tóm tắt các khái niệm chính

• Động năng: Là năng lượng mà một vật có được do chuyển động. Công thức tính động năng là \( W_{đ} = \frac{1}{2}mv^2 \), trong đó \( m \) là khối lượng của vật và \( v \) là vận tốc.
• Thế năng: Là năng lượng của một vật do vị trí của nó trong trường lực. Công thức tính thế năng trọng trường là \( W_t = mgh \), trong đó \( m \) là khối lượng, \( g \) là gia tốc trọng trường và \( h \) là độ cao.

2. Các dạng bài tập trọng tâm

1. Bài tập tính động năng và thế năng từ các công thức cơ bản.
2. Bài tập áp dụng định luật bảo toàn năng lượng để giải các bài toán liên quan đến động năng và thế năng.
3. Bài tập kết hợp giữa động năng và thế năng trong các bài toán thực tế như chuyển động trên mặt phẳng nghiêng, chuyển động ném xiên, v.v.

3. Lời khuyên khi học Vật Lý 10 Bài 25

• Nắm vững công thức và hiểu rõ ý nghĩa của từng đại lượng trong công thức.
• Rèn luyện tư duy phân tích bài toán bằng cách phân biệt rõ các loại năng lượng và điều kiện bảo toàn năng lượng trong từng trường hợp.
• Thực hành giải các bài tập mẫu và thử thách bản thân với các bài tập nâng cao để củng cố kiến thức.

Hy vọng rằng các kiến thức trên sẽ giúp bạn tự tin hơn khi làm các bài tập về động năng và thế năng trong bài học này.