Động Năng Bằng 3/4 Cơ Năng: Bí Quyết Tối Ưu Hóa Cơ Học

Trong vật lý, khái niệm "động năng bằng 3/4 cơ năng" thường được thảo luận trong bối cảnh của dao động điều hòa, đặc biệt là khi nói về các hệ dao động như con lắc đơn hoặc con lắc lò xo. Đây là một tình huống điển hình khi một vật dao động, và ta xét mối quan hệ giữa động năng, thế năng và cơ năng tổng cộng của hệ.

1. Khái Niệm Cơ Bản

Cơ năng của một hệ dao động bao gồm hai thành phần chính:

• Động năng (Kinetic Energy): Là năng lượng mà vật có được do chuyển động. Động năng của một vật dao động điều hòa có thể được tính bằng công thức \( W_d = \frac{1}{2} m v^2 \).
• Thế năng (Potential Energy): Là năng lượng dự trữ của vật do vị trí của nó trong một trường lực, chẳng hạn như trọng lực. Thế năng của vật dao động có thể được tính bằng công thức \( W_t = \frac{1}{2} k x^2 \) (với con lắc lò xo) hoặc \( W_t = mgh \) (với con lắc đơn).

2. Quan Hệ Giữa Động Năng và Cơ Năng

Trong hệ dao động điều hòa, tổng của động năng và thế năng luôn bằng cơ năng tổng cộng (E):

\( E = W_d + W_t \)

Khi vật ở vị trí mà động năng bằng 3/4 cơ năng, ta có:

\( W_d = \frac{3}{4} E \)

Lúc này, thế năng của hệ sẽ là:

\( W_t = E - W_d = \frac{1}{4} E \)

3. Ví Dụ Cụ Thể

Giả sử một vật dao động điều hòa với biên độ \( A \), cơ năng của hệ là:

\( E = \frac{1}{2} k A^2 \)

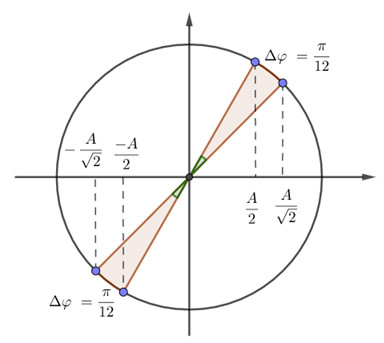
Khi động năng bằng 3/4 cơ năng, vật sẽ cách vị trí cân bằng một khoảng \( x \) mà tại đó:

\( \frac{1}{2} m \omega^2 (A^2 - x^2) = \frac{3}{4} \times \frac{1}{2} m \omega^2 A^2 \)

Giải phương trình trên, ta có thể tìm ra giá trị của \( x \), là khoảng cách từ vị trí cân bằng mà tại đó động năng bằng 3/4 cơ năng.

4. Ứng Dụng Thực Tiễn

Kiến thức về sự chuyển hóa năng lượng trong dao động điều hòa, đặc biệt là mối quan hệ giữa động năng và cơ năng, rất quan trọng trong nhiều ứng dụng thực tiễn như trong kỹ thuật cơ khí, thiết kế hệ thống treo, và trong nghiên cứu khoa học về sóng và dao động.

5. Bài Tập Vận Dụng

Để hiểu rõ hơn về mối quan hệ này, người học có thể thực hành qua các bài tập liên quan đến tính toán động năng, thế năng và cơ năng trong các hệ dao động khác nhau.

• Bài tập 1: Một vật dao động với biên độ 10 cm. Tìm khoảng cách từ vị trí cân bằng khi động năng của vật bằng 3/4 cơ năng.
• Bài tập 2: Một con lắc đơn dao động với cơ năng 20 J. Tìm giá trị động năng và thế năng khi động năng bằng 15 J.

Trong lĩnh vực vật lý, động năng và cơ năng là hai khái niệm cơ bản và quan trọng. Động năng là năng lượng mà một vật sở hữu do chuyển động của nó, được tính bằng công thức:

\[ K = \frac{1}{2} mv^2 \]

trong đó \(m\) là khối lượng của vật và \(v\) là vận tốc của nó. Động năng phụ thuộc trực tiếp vào khối lượng và vận tốc của vật, nghĩa là nếu vận tốc tăng gấp đôi, động năng sẽ tăng gấp bốn.

Cơ năng, mặt khác, là tổng của động năng và thế năng, đại diện cho toàn bộ năng lượng mà một hệ có được nhờ vào vị trí và chuyển động của các phần tử trong hệ đó. Khi động năng bằng 3/4 cơ năng, điều này cho thấy sự cân bằng giữa các thành phần của năng lượng trong hệ dao động, một trạng thái đặc biệt trong nghiên cứu vật lý.

Hiểu rõ mối quan hệ giữa động năng và cơ năng giúp giải quyết nhiều bài toán vật lý phức tạp, từ đó ứng dụng vào các lĩnh vực thực tế như cơ học, kỹ thuật, và khoa học ứng dụng.

Để tính động năng và cơ năng của một vật, ta cần hiểu rõ công thức và các yếu tố liên quan. Dưới đây là cách tính toán chi tiết:

• Động năng (K): Động năng của một vật được tính bằng công thức: \[ K = \frac{1}{2} mv^2 \] Trong đó:
  • \(m\) là khối lượng của vật (đơn vị: kg).
  • \(v\) là vận tốc của vật (đơn vị: m/s).
  Công thức này cho thấy động năng phụ thuộc vào cả khối lượng và vận tốc của vật. Khi vận tốc tăng lên, động năng cũng tăng theo tỷ lệ bình phương.
• Cơ năng (E): Cơ năng của một hệ là tổng của động năng và thế năng, được tính bằng công thức: \[ E = K + U \] Trong đó:
  • \(K\) là động năng của hệ.
  • \(U\) là thế năng của hệ.
  Thế năng \(U\) có thể là thế năng hấp dẫn hoặc thế năng đàn hồi, tùy thuộc vào hệ đang xét.

Trường hợp đặc biệt khi động năng bằng 3/4 cơ năng:

• Khi động năng \(K\) bằng 3/4 cơ năng \(E\), ta có: \[ K = \frac{3}{4} E \] Dẫn đến: \[ E = \frac{4}{3} K \] Điều này có nghĩa là thế năng \(U\) sẽ chiếm 1/4 cơ năng: \[ U = \frac{1}{4} E \] Sự phân bố này thường xuất hiện trong các bài toán dao động điều hòa và các hệ vật lý khác.

Mối quan hệ giữa động năng và cơ năng, đặc biệt trong trường hợp động năng bằng 3/4 cơ năng, không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng trong thực tế, từ cơ học đến kỹ thuật và khoa học.

• Cơ học và Kỹ thuật: Trong các hệ thống cơ học, như máy móc hoặc cơ cấu truyền động, việc hiểu rõ tỷ lệ động năng và cơ năng giúp tối ưu hóa hiệu suất hoạt động. Ví dụ, trong các hệ thống giảm chấn, việc phân bổ động năng và cơ năng hợp lý giúp kiểm soát sự rung động và ổn định của hệ thống.
• Hệ thống dao động: Trong các hệ thống dao động điều hòa như con lắc hay lò xo, tỷ lệ giữa động năng và cơ năng là yếu tố quan trọng để phân tích và dự đoán hành vi của hệ thống qua các chu kỳ dao động. Điều này áp dụng trong việc thiết kế các thiết bị chống rung hay các hệ thống cân bằng tự động.
• Năng lượng tái tạo: Trong các dự án liên quan đến năng lượng tái tạo, như tua-bin gió hay pin mặt trời, việc quản lý và chuyển đổi năng lượng từ một dạng này sang dạng khác, giữa động năng và cơ năng, là chìa khóa để tối ưu hóa hiệu suất khai thác năng lượng từ các nguồn tự nhiên.
• Giáo dục và Nghiên cứu: Mối quan hệ giữa động năng và cơ năng cũng là nền tảng trong giáo dục và nghiên cứu khoa học. Nó giúp học sinh, sinh viên hiểu rõ hơn về các nguyên lý vật lý cơ bản, từ đó phát triển các kỹ năng phân tích và giải quyết vấn đề trong học tập và nghiên cứu.

Việc áp dụng kiến thức về động năng và cơ năng vào thực tế không chỉ giúp cải thiện hiệu suất trong các lĩnh vực công nghiệp mà còn góp phần vào sự phát triển bền vững và tối ưu hóa tài nguyên.

Phần này cung cấp các bài tập thực hành để củng cố kiến thức về động năng, cơ năng và mối quan hệ giữa chúng, đặc biệt là trong trường hợp động năng bằng 3/4 cơ năng. Các bài tập này bao gồm nhiều dạng khác nhau, từ cơ bản đến nâng cao, giúp người học nắm vững lý thuyết và áp dụng vào thực tế.

4.1. Bài Tập Tính Toán Động Năng và Cơ Năng

1. Một vật có khối lượng m = 2 kg đang chuyển động với vận tốc v = 3 m/s. Tính động năng của vật.

   Hướng dẫn: Áp dụng công thức động năng W_đ = 1/2 * m * v², ta có:

   W_đ = 1/2 * 2 * 3² = 9 J

2. Một vật có khối lượng m = 5 kg, được nâng lên độ cao h = 10 m so với mặt đất. Tính cơ năng của vật khi nó đứng yên ở độ cao này.

   Hướng dẫn: Cơ năng W_c bằng tổng động năng và thế năng. Ở đây, vì vật đứng yên nên động năng bằng 0. Thế năng được tính bằng W_t = mgh. Vậy:

   W_t = 5 * 9,8 * 10 = 490 J

   W_c = W_t = 490 J

4.2. Bài Tập Vận Dụng Quan Hệ Giữa Động Năng và Cơ Năng

1. Một vật có khối lượng m = 4 kg chuyển động với vận tốc v sao cho động năng của vật bằng 3/4 cơ năng của nó. Biết cơ năng của vật là 100 J. Tính vận tốc v.

   Hướng dẫn: Đặt W_đ là động năng và W_c là cơ năng. Theo đề bài, ta có:

   W_đ = 3/4 * W_c = 3/4 * 100 = 75 J

   Áp dụng công thức W_đ = 1/2 * m * v², ta có:

   75 = 1/2 * 4 * v²

   v² = 75 / 2 = 37,5

   v = √37,5 ≈ 6,12 m/s

2. Một vật được ném thẳng đứng lên cao với vận tốc ban đầu v₀. Khi vật đạt tới một độ cao nào đó, động năng của nó bằng 3/4 cơ năng. Tìm độ cao này.

   Hướng dẫn: Tính cơ năng tại điểm ném và áp dụng công thức bảo toàn cơ năng để tìm độ cao cần thiết.

4.3. Bài Tập Tự Rèn Luyện

Các bài tập dưới đây yêu cầu học viên tự giải quyết để nâng cao kỹ năng:

• Một quả bóng có khối lượng 0,5 kg được ném thẳng đứng lên với vận tốc 10 m/s. Tính cơ năng tại điểm ném và động năng, thế năng tại điểm cao nhất mà quả bóng đạt được.
• Một vật chuyển động trên mặt phẳng ngang với vận tốc 5 m/s, sau đó lên một dốc cao. Tính vận tốc của vật khi động năng bằng 3/4 cơ năng, biết khối lượng của vật là 2 kg.

Khi giải bài tập liên quan đến động năng và cơ năng, đặc biệt trong các tình huống động năng bằng 3/4 cơ năng, người học cần chú ý các điểm sau để đảm bảo tính chính xác và hiệu quả trong quá trình làm bài.

5.1. Cách Nhận Biết Động Năng Bằng 3/4 Cơ Năng

1. Xác định đúng công thức: Trong các bài toán, cần nhận diện chính xác mối quan hệ giữa động năng và cơ năng, đặc biệt là khi đề bài yêu cầu tính toán khi động năng bằng 3/4 cơ năng. Công thức cần nhớ là:

   W_đ = 3/4 * W_c

2. Tính toán từng bước: Khi đã có mối quan hệ trên, hãy giải quyết từng phần của bài toán: tính cơ năng trước, sau đó áp dụng công thức để tính động năng, rồi giải các bước tiếp theo như tìm vận tốc, độ cao, hoặc vị trí.

3. Lưu ý về đơn vị: Đảm bảo rằng các đơn vị được sử dụng trong bài toán đều đồng nhất (ví dụ: khối lượng tính bằng kg, vận tốc bằng m/s, và năng lượng bằng J).

5.2. Sai Lầm Thường Gặp Khi Tính Toán

• Nhầm lẫn giữa động năng và thế năng: Một trong những sai lầm phổ biến là nhầm lẫn giữa động năng và thế năng. Động năng liên quan đến chuyển động, trong khi thế năng thường liên quan đến vị trí và trọng lực. Luôn nhớ kiểm tra kỹ các giá trị và công thức sử dụng.

• Bỏ qua lực ma sát hoặc các lực khác: Trong một số bài toán thực tế, lực ma sát hoặc các lực khác có thể ảnh hưởng đến tổng cơ năng của hệ. Nếu không được đề cập trong đề bài, bạn có thể bỏ qua, nhưng trong các bài toán phức tạp hơn, cần tính đến để có kết quả chính xác.

• Sử dụng sai công thức: Đảm bảo bạn hiểu rõ và sử dụng đúng công thức cho từng phần của bài toán. Nếu không, kết quả sẽ sai lệch đáng kể. Đặc biệt, chú ý rằng công thức liên hệ giữa động năng và cơ năng không áp dụng cho mọi loại bài toán, chỉ áp dụng khi có sự tương đồng hoặc yêu cầu cụ thể trong đề bài.