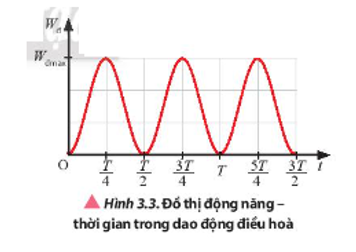
Chủ đề động năng quay: Động năng quay là một khái niệm quan trọng trong vật lý học, đóng vai trò quan trọng trong các ứng dụng công nghiệp và đời sống. Bài viết này sẽ giúp bạn hiểu rõ hơn về động năng quay, từ định nghĩa cơ bản, công thức tính toán cho đến các ví dụ và bài tập minh họa cụ thể.
Mục lục
Động Năng Quay
Động năng quay là một khái niệm quan trọng trong vật lý, đặc biệt liên quan đến chuyển động của các vật thể rắn quanh một trục cố định. Động năng quay có vai trò quan trọng trong nhiều lĩnh vực khoa học và công nghệ, từ cơ học cổ điển cho đến các ứng dụng công nghiệp.
Định Nghĩa Động Năng Quay
Động năng quay của một vật rắn được tính theo công thức:
\[
T = \frac{1}{2} I \omega^2
\]
Trong đó:
- I là mômen quán tính của vật đối với trục quay.
- ω là tốc độ góc của vật quanh trục cố định.
Ứng Dụng Của Động Năng Quay
- Trong các máy móc công nghiệp, động năng quay có thể chuyển hóa thành công việc làm.
- Động năng quay giúp giải quyết các vấn đề liên quan đến chuyển động xoay trong các thiết bị cơ khí.
- Được sử dụng trong nghiên cứu về cơ học cổ điển và vật lý hạt nhân.
Các Bài Tập Về Động Năng Quay
Dưới đây là một số bài tập tiêu biểu về động năng quay:
- Xác định động năng quay của một đĩa tròn đặc với khối lượng m = 5kg, đường kính 0,6m, quay quanh trục cố định đi qua tâm.
- Tính toán độ biến thiên động năng khi tốc độ góc của một vật thay đổi từ ω1 đến ω2.
- Ứng dụng nguyên tắc bảo toàn động năng quay để giải quyết bài toán liên quan đến hệ thống cơ học.
Ví Dụ Thực Tế
Một ví dụ điển hình của động năng quay là trong các tua-bin gió, nơi năng lượng từ gió làm quay các cánh quạt, từ đó tạo ra động năng quay và được chuyển đổi thành điện năng.
Kết Luận
Động năng quay là một khía cạnh quan trọng của động học, với nhiều ứng dụng thực tế trong đời sống và công nghiệp. Hiểu biết về động năng quay không chỉ giúp cải thiện hiệu suất của các thiết bị cơ khí mà còn đóng vai trò trong việc phát triển các công nghệ mới.

.png)
Giới Thiệu Về Động Năng Quay
Động năng quay là một dạng năng lượng cơ học liên quan đến chuyển động quay của một vật rắn quanh trục cố định. Khi một vật quay, các điểm trên vật sẽ di chuyển với các vận tốc khác nhau tùy thuộc vào khoảng cách từ trục quay. Động năng quay mô tả tổng năng lượng của các chuyển động này, và được tính toán bằng cách sử dụng mômen quán tính và vận tốc góc.
Để hiểu rõ hơn, ta có thể xem xét công thức tính động năng quay:
\[
T = \frac{1}{2} I \omega^2
\]
Trong đó:
- I là mômen quán tính của vật đối với trục quay.
- ω là vận tốc góc của vật.
Mômen quán tính, ký hiệu là I, phụ thuộc vào cách phân bố khối lượng của vật quanh trục quay. Vật có mômen quán tính càng lớn thì càng khó thay đổi trạng thái quay của nó, tức là cần nhiều năng lượng hơn để đạt được cùng một vận tốc góc.
Động năng quay xuất hiện trong nhiều ứng dụng thực tế, từ các thiết bị cơ khí như bánh răng và động cơ, đến các hệ thống năng lượng như tua-bin gió. Hiểu biết về động năng quay giúp cải thiện hiệu suất và an toàn trong các lĩnh vực này.
Nguyên Tắc Bảo Toàn Động Năng Quay
Nguyên tắc bảo toàn động năng quay là một trong những định luật cơ bản của cơ học cổ điển, đóng vai trò quan trọng trong việc hiểu và phân tích các hệ thống vật lý liên quan đến chuyển động quay. Theo nguyên tắc này, tổng động năng quay của một hệ thống kín (không chịu tác động của lực ngoài) sẽ được bảo toàn trong quá trình chuyển động, tức là không bị mất mát hay tăng thêm.
Để diễn giải nguyên tắc bảo toàn động năng quay, ta có thể biểu diễn qua công thức sau:
\[
T_1 = T_2
\]
Trong đó:
- T_1 là động năng quay ban đầu của hệ thống.
- T_2 là động năng quay sau quá trình biến đổi.
Nếu một hệ thống quay không chịu tác động từ bên ngoài, mômen quán tính và vận tốc góc của hệ thống sẽ điều chỉnh sao cho động năng quay của hệ luôn được giữ nguyên. Điều này thường được thấy trong các hiện tượng vật lý như con quay hồi chuyển hoặc trong cơ học thiên thể khi mômen quán tính thay đổi nhưng động năng quay tổng thể vẫn không đổi.
Ví dụ điển hình của nguyên tắc bảo toàn động năng quay là khi một vũ công trượt băng kéo tay vào gần cơ thể để quay nhanh hơn. Khi mômen quán tính giảm (do việc kéo tay lại), vận tốc góc của người trượt tăng lên, nhưng tổng động năng quay vẫn được bảo toàn.
Nguyên tắc bảo toàn động năng quay được ứng dụng trong nhiều lĩnh vực như cơ học, kỹ thuật, và thiên văn học. Nó giúp các nhà khoa học và kỹ sư thiết kế các hệ thống ổn định, tính toán chính xác các chuyển động phức tạp và giải quyết các bài toán liên quan đến động lực học của các hệ thống quay.

Các Dạng Bài Tập Về Động Năng Quay
Dưới đây là các dạng bài tập về động năng quay, kèm theo phương pháp giải chi tiết:
Bài Tập Tính Toán Động Năng Quay
Loại bài tập này yêu cầu tính toán động năng quay của các vật thể dựa trên các thông số như mô men quán tính và vận tốc góc.
- Dạng 1: Tính động năng quay của một vật rắn quay quanh một trục cố định
- Đề bài: Tính động năng quay của một bánh xe có mô men quán tính I quay với tốc độ góc ω.
- Giải: Sử dụng công thức K = ½ Iω² để tính động năng quay.
- Ví dụ: Một bánh xe có mô men quán tính I = 0.5 kg·m² và tốc độ góc ω = 10 rad/s, động năng quay sẽ là K = ½ × 0.5 × 10² = 25 J.
- Dạng 2: Bài tập kết hợp động năng quay và động năng tịnh tiến
- Đề bài: Một hình trụ đặc có khối lượng m lăn không trượt trên mặt phẳng ngang với tốc độ của khối tâm v. Tính tổng động năng.
- Giải: Tổng động năng là tổng của động năng tịnh tiến và động năng quay. Sử dụng công thức K = ½ mv² + ½ Iω², trong đó I = ½ mr² và ω = v/r.
- Ví dụ: Với m = 10 kg, v = 2 m/s, tổng động năng sẽ là K = ½ × 10 × 2² + ½ × ½ × 10 × (2/1)² = 30 J.
Bài Tập Vận Dụng Nguyên Tắc Bảo Toàn Động Năng Quay
Những bài tập này tập trung vào việc áp dụng nguyên tắc bảo toàn động năng quay trong các hệ kín.
- Dạng 1: Bài tập về bảo toàn động năng trong hệ kín
- Đề bài: Hai vật rắn quay với các mô men quán tính I₁ và I₂ và tốc độ góc ω₁ và ω₂ tương ứng. Sau khi kết nối chúng bằng một khớp nối, tính tốc độ góc chung ω.
- Giải: Sử dụng bảo toàn động năng: I₁ω₁²/2 + I₂ω₂²/2 = (I₁ + I₂)ω²/2. Từ đó giải ra ω.
- Ví dụ: Nếu I₁ = 2 kg·m², ω₁ = 3 rad/s, I₂ = 3 kg·m², ω₂ = 2 rad/s, thì tốc độ góc chung ω là ω = √[(2×3² + 3×2²)/(2 + 3)] ≈ 2.45 rad/s.

Ví Dụ Thực Tế Về Động Năng Quay
Động năng quay có nhiều ứng dụng trong đời sống và công nghiệp. Dưới đây là một số ví dụ cụ thể về cách động năng quay được áp dụng trong thực tế:
1. Động Năng Quay Trong Các Thiết Bị Cơ Khí
Trong các thiết bị cơ khí như động cơ và máy móc công nghiệp, động năng quay là yếu tố quan trọng giúp chuyển đổi năng lượng cơ học thành công việc hữu ích. Ví dụ, khi một động cơ quay, động năng quay của nó được chuyển hóa thành lực kéo để di chuyển các bộ phận khác của máy, tạo ra công suất cần thiết cho hoạt động của thiết bị.
2. Động Năng Quay Trong Tua-bin Gió
Tua-bin gió là một ví dụ điển hình về việc sử dụng động năng quay trong năng lượng tái tạo. Khi gió thổi qua các cánh quạt của tua-bin, nó làm cho các cánh quạt quay, và động năng quay này được chuyển hóa thành điện năng thông qua máy phát điện. Điều này cho phép chúng ta khai thác năng lượng gió để cung cấp điện một cách bền vững và hiệu quả.
3. Ứng Dụng Trong Đời Sống Hàng Ngày
Một ví dụ đơn giản nhưng thiết thực của động năng quay là trong các thiết bị như máy giặt. Trong quá trình vắt khô quần áo, lồng giặt quay với tốc độ cao để tạo ra lực ly tâm, nhờ đó nước được ép ra khỏi vải, giúp quần áo nhanh khô hơn.
4. Động Năng Quay Trong Thể Thao
Trong các môn thể thao như bóng đá, cầu thủ thường sử dụng kỹ thuật sút bóng xoáy. Khi bóng quay, động năng quay giúp quả bóng bay với một đường cong nhất định, gây khó khăn cho thủ môn trong việc bắt bóng. Đây là minh chứng cho ứng dụng thực tế của động năng quay trong thể thao.