Chủ đề vận tốc hạt nhân: Vận tốc và tốc độ là hai khái niệm thường bị nhầm lẫn trong vật lý học. Bài viết này sẽ giải thích sự khác biệt giữa vận tốc và tốc độ, giúp bạn hiểu rõ hơn về bản chất của chúng. Tốc độ chỉ đo lường độ lớn của sự chuyển động, trong khi vận tốc còn bao gồm cả hướng di chuyển.
Mục lục
Vận Tốc Khác Tốc Độ Như Thế Nào?
Vận tốc và tốc độ là hai khái niệm quan trọng trong vật lý, thường bị nhầm lẫn với nhau. Dưới đây là sự khác biệt chi tiết giữa vận tốc và tốc độ:
1. Khái Niệm Vận Tốc
Vận tốc là đại lượng vật lý biểu thị tốc độ di chuyển của một vật theo một hướng cụ thể. Nó là một vector, có nghĩa là ngoài độ lớn, nó còn có hướng. Công thức tính vận tốc được biểu diễn bằng:
\[
\vec{v} = \frac{\Delta \vec{x}}{\Delta t}
\]
Trong đó:
- \(\vec{v}\) là vận tốc
- \(\Delta \vec{x}\) là độ dời (sự thay đổi vị trí) của vật
- \(\Delta t\) là khoảng thời gian
2. Khái Niệm Tốc Độ
Tốc độ là đại lượng vật lý biểu thị khoảng cách mà một vật di chuyển được trong một khoảng thời gian. Tốc độ là một đại lượng vô hướng, chỉ có độ lớn và không có hướng. Công thức tính tốc độ được biểu diễn bằng:
\[
v = \frac{s}{t}
\]
Trong đó:
- \(v\) là tốc độ
- \(s\) là quãng đường đi được
- \(t\) là thời gian di chuyển
3. Sự Khác Biệt Chính Giữa Vận Tốc và Tốc Độ
- Bản Chất: Vận tốc là một đại lượng vector, trong khi tốc độ là một đại lượng vô hướng.
- Hướng: Vận tốc có hướng, còn tốc độ thì không.
- Công Thức: Vận tốc tính dựa trên độ dời và thời gian, trong khi tốc độ tính dựa trên quãng đường và thời gian.
- Ý Nghĩa: Vận tốc cho biết mức độ nhanh chóng và hướng di chuyển của vật, trong khi tốc độ chỉ cho biết mức độ nhanh chóng mà không quan tâm đến hướng.
4. Ví Dụ Minh Họa
Giả sử một chiếc xe di chuyển từ điểm A đến điểm B cách nhau 100 km về phía Đông trong 2 giờ. Khi đó:
- Tốc độ: Tốc độ của xe là \(v = \frac{100 \text{ km}}{2 \text{ giờ}} = 50 \text{ km/h}\).
- Vận tốc: Vận tốc của xe là \(\vec{v} = \frac{100 \text{ km về phía Đông}}{2 \text{ giờ}} = 50 \text{ km/h về phía Đông}\).
Như vậy, sự khác biệt giữa vận tốc và tốc độ không chỉ nằm ở cách chúng được tính toán mà còn ở ý nghĩa vật lý của chúng. Hiểu rõ sự khác biệt này giúp ta áp dụng đúng đắn trong các bài toán vật lý cũng như trong thực tế.

.png)
1. Khái Niệm Cơ Bản
Để hiểu rõ sự khác biệt giữa vận tốc và tốc độ, chúng ta cần bắt đầu từ các khái niệm cơ bản trong vật lý học:
- Tốc độ: Tốc độ là một đại lượng vô hướng, chỉ đơn giản đo lường độ lớn của sự thay đổi vị trí của một đối tượng trong một khoảng thời gian. Công thức tính tốc độ là:
\[
v = \frac{s}{t}
\]
Trong đó:
- \(v\): Tốc độ (m/s)
- \(s\): Quãng đường đi được (m)
- \(t\): Thời gian (s)
- Vận tốc: Vận tốc là một đại lượng vector, không chỉ đo lường độ lớn của sự thay đổi vị trí mà còn bao gồm cả hướng di chuyển. Công thức tính vận tốc là:
\[
\vec{v} = \frac{\vec{d}}{t}
\]
Trong đó:
- \(\vec{v}\): Vận tốc (m/s)
- \(\vec{d}\): Độ dời, hay khoảng cách di chuyển có hướng (m)
- \(t\): Thời gian (s)
Để dễ hiểu hơn, chúng ta có thể so sánh tốc độ và vận tốc qua bảng sau:
| Tham số | Tốc độ | Vận tốc |
|---|---|---|
| Định nghĩa | Độ lớn của sự thay đổi vị trí của đối tượng | Độ lớn và hướng của sự thay đổi vị trí của đối tượng |
| Loại đại lượng | Vô hướng | Vector |
| Giá trị | Không âm | Có thể âm |
| Ví dụ | Một chiếc xe chạy 60 km/h | Một chiếc xe chạy 60 km/h về hướng bắc |
Như vậy, tốc độ chỉ đơn thuần là thước đo độ nhanh, trong khi vận tốc còn bao gồm cả hướng đi của đối tượng. Việc nắm vững khái niệm này giúp chúng ta hiểu rõ hơn về cách chuyển động trong thực tế.
2. Sự Khác Biệt Giữa Tốc Độ Và Vận Tốc
Để hiểu rõ hơn về sự khác biệt giữa tốc độ và vận tốc, chúng ta cần phân tích từng khía cạnh cụ thể của hai khái niệm này:
- Định nghĩa:
- Tốc độ: Là đại lượng vô hướng, chỉ đơn thuần đo lường độ lớn của quãng đường đi được trong một khoảng thời gian. Công thức tính tốc độ là: \[ v = \frac{s}{t} \]
- Vận tốc: Là đại lượng vector, đo lường cả độ lớn và hướng của sự di chuyển. Công thức tính vận tốc là: \[ \vec{v} = \frac{\vec{d}}{t} \]
- Phân loại:
- Tốc độ: Đại lượng vô hướng, chỉ có độ lớn, không có hướng.
- Vận tốc: Đại lượng vector, bao gồm cả độ lớn và hướng.
- Tính chất:
- Tốc độ: Luôn không âm, chỉ biểu thị sự nhanh chậm của chuyển động.
- Vận tốc: Có thể âm, dương hoặc bằng không, biểu thị sự thay đổi vị trí theo hướng xác định.
- Ví dụ:
- Tốc độ: Một xe chạy với tốc độ 60 km/h.
- Vận tốc: Một xe chạy với vận tốc 60 km/h về hướng bắc.
Dưới đây là bảng so sánh sự khác biệt giữa tốc độ và vận tốc:
| Tham số | Tốc độ | Vận tốc |
|---|---|---|
| Định nghĩa | Độ lớn của quãng đường đi được trong một khoảng thời gian | Độ lớn và hướng của sự di chuyển trong một khoảng thời gian |
| Loại đại lượng | Vô hướng | Vector |
| Tính chất | Không âm | Có thể âm, dương hoặc bằng không |
| Ví dụ | Một xe chạy 60 km/h | Một xe chạy 60 km/h về hướng bắc |
Qua bảng so sánh và các ví dụ trên, chúng ta có thể thấy rằng tốc độ chỉ đo lường độ lớn của chuyển động, trong khi vận tốc cung cấp thông tin đầy đủ hơn về cả độ lớn và hướng của sự di chuyển.

3. Ví Dụ Minh Họa
Để hiểu rõ hơn về sự khác biệt giữa tốc độ và vận tốc, chúng ta hãy xem xét các ví dụ minh họa dưới đây:
- Ví dụ 1:
Một chiếc xe chạy trên một con đường thẳng với vận tốc không đổi. Nếu chiếc xe này đi từ điểm A đến điểm B với quãng đường \( s = 100 \) km trong thời gian \( t = 2 \) giờ, thì:
- Tốc độ: \[ v = \frac{s}{t} = \frac{100 \text{ km}}{2 \text{ giờ}} = 50 \text{ km/h} \]
- Vận tốc: Nếu điểm B nằm về hướng Đông của điểm A, thì: \[ \vec{v} = \frac{\vec{d}}{t} = \frac{100 \text{ km Đông}}{2 \text{ giờ}} = 50 \text{ km/h Đông} \]
- Ví dụ 2:
Một người đi bộ quanh một vòng tròn với bán kính \( r = 10 \) m. Nếu người đó hoàn thành một vòng trong \( t = 1 \) phút (60 giây), thì:
- Tốc độ: Chu vi của vòng tròn là \( C = 2\pi r = 2\pi \times 10 = 62.83 \) m. Vậy: \[ v = \frac{C}{t} = \frac{62.83 \text{ m}}{60 \text{ s}} = 1.05 \text{ m/s} \]
- Vận tốc: Vì người đi bộ quay lại vị trí ban đầu, nên độ dời (displacement) là \( \vec{d} = 0 \). Do đó: \[ \vec{v} = \frac{\vec{d}}{t} = \frac{0}{60 \text{ s}} = 0 \text{ m/s} \]
- Ví dụ 3:
Một máy bay bay từ Hà Nội đến Thành phố Hồ Chí Minh. Giả sử khoảng cách giữa hai thành phố là \( d = 1,700 \) km và thời gian bay là \( t = 2 \) giờ, thì:
- Tốc độ: \[ v = \frac{d}{t} = \frac{1,700 \text{ km}}{2 \text{ giờ}} = 850 \text{ km/h} \]
- Vận tốc: Nếu máy bay bay theo hướng Nam, thì: \[ \vec{v} = \frac{\vec{d}}{t} = \frac{1,700 \text{ km Nam}}{2 \text{ giờ}} = 850 \text{ km/h Nam} \]
Những ví dụ trên giúp làm rõ sự khác biệt giữa tốc độ và vận tốc trong các tình huống thực tế. Tốc độ chỉ đo lường độ lớn của chuyển động, trong khi vận tốc cung cấp thông tin đầy đủ về cả độ lớn và hướng của sự di chuyển.

4. Ứng Dụng Thực Tiễn
Hiểu rõ sự khác biệt giữa tốc độ và vận tốc có ý nghĩa quan trọng trong nhiều lĩnh vực thực tiễn. Dưới đây là một số ứng dụng cụ thể của khái niệm này:
- Giao thông vận tải:
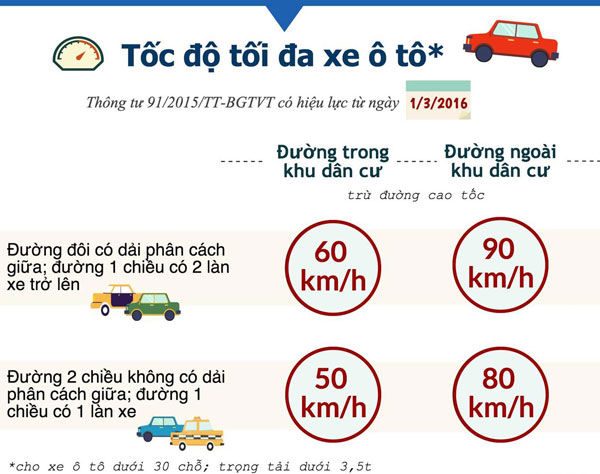
Trong giao thông vận tải, cả tốc độ và vận tốc đều được sử dụng để đảm bảo an toàn và hiệu quả. Chẳng hạn, giới hạn tốc độ trên đường cao tốc được đặt ra để kiểm soát tốc độ của các phương tiện nhằm giảm nguy cơ tai nạn. Đồng thời, vận tốc cũng được tính đến khi lập kế hoạch hành trình để tối ưu hóa thời gian di chuyển và nhiên liệu.
- Hàng không:
Trong ngành hàng không, phi công phải nắm vững cả tốc độ và vận tốc để điều khiển máy bay một cách an toàn. Tốc độ không khí ảnh hưởng đến lực nâng và lực cản, trong khi vận tốc thực (ground speed) giúp xác định vị trí và thời gian đến đích.
- Khoa học và nghiên cứu:
Trong nghiên cứu khoa học, vận tốc được sử dụng để mô tả chuyển động của các vật thể trong các thí nghiệm và nghiên cứu. Ví dụ, trong vật lý học, vận tốc được sử dụng để tính toán quỹ đạo và dự đoán chuyển động của các thiên thể.
- Thể thao:
Trong thể thao, đặc biệt là các môn đua xe và điền kinh, vận tốc và tốc độ được sử dụng để đánh giá hiệu suất của vận động viên. Hiểu rõ khái niệm này giúp cải thiện kỹ thuật và chiến thuật thi đấu.
- Kỹ thuật:
Trong kỹ thuật, việc tính toán vận tốc của các bộ phận chuyển động trong máy móc giúp đảm bảo hoạt động trơn tru và hiệu quả. Ví dụ, vận tốc của các bánh răng trong một hệ thống truyền động phải được tối ưu hóa để giảm hao mòn và tăng tuổi thọ của thiết bị.
Các ứng dụng trên cho thấy sự hiểu biết về tốc độ và vận tốc không chỉ là lý thuyết mà còn mang lại lợi ích thiết thực trong cuộc sống hàng ngày và công việc.

5. Phương Pháp Tính Toán
Để hiểu rõ hơn về phương pháp tính toán vận tốc và tốc độ, chúng ta cần xem xét một số công thức và ví dụ cụ thể.
1. Tính Toán Tốc Độ
Tốc độ được tính bằng công thức:
\[ \text{Tốc độ} = \frac{\text{Quãng đường}}{\text{Thời gian}} \]
Ví dụ: Nếu một chiếc xe di chuyển được quãng đường 100 km trong 2 giờ, tốc độ của nó sẽ là:
\[ \text{Tốc độ} = \frac{100 \text{ km}}{2 \text{ giờ}} = 50 \text{ km/h} \]
2. Tính Toán Vận Tốc
Vận tốc không chỉ quan tâm đến độ lớn mà còn cả hướng di chuyển. Vận tốc được tính bằng công thức:
\[ \vec{v} = \frac{\Delta \vec{x}}{\Delta t} \]
Trong đó:
- \(\vec{v}\) là vận tốc
- \(\Delta \vec{x}\) là độ dời (véc tơ quãng đường)
- \(\Delta t\) là thời gian
Ví dụ: Một người đi bộ theo hướng Đông được 3 km trong 1 giờ, vận tốc của người đó là:
\[ \vec{v} = \frac{3 \text{ km Đông}}{1 \text{ giờ}} = 3 \text{ km/h Đông} \]
3. Vận Tốc Trung Bình
Vận tốc trung bình được tính bằng cách chia tổng độ dời cho tổng thời gian:
\[ v_{\text{tb}} = \frac{\Delta x_{\text{tổng}}}{\Delta t_{\text{tổng}}} \]
Ví dụ: Nếu một vật thể di chuyển từ điểm A đến điểm B, với độ dời tổng cộng là 80 km trong 4 giờ, thì vận tốc trung bình là:
\[ v_{\text{tb}} = \frac{80 \text{ km}}{4 \text{ giờ}} = 20 \text{ km/h} \]
4. Vận Tốc Tức Thời
Vận tốc tức thời là vận tốc tại một thời điểm cụ thể và được xác định bằng đạo hàm của độ dời theo thời gian:
\[ v = \frac{dx}{dt} \]
Ví dụ: Nếu đồ thị độ dời theo thời gian là một đường thẳng, đạo hàm của độ dời theo thời gian sẽ cho chúng ta vận tốc tức thời.
5. So Sánh Tốc Độ và Vận Tốc
Trong thực tế, tốc độ chỉ là một đại lượng vô hướng, không có hướng, trong khi vận tốc là một đại lượng có hướng. Điều này có nghĩa là hai đối tượng có thể có cùng tốc độ nhưng vận tốc khác nhau nếu chúng di chuyển theo các hướng khác nhau.
Hy vọng rằng những phương pháp tính toán và ví dụ trên đã giúp bạn hiểu rõ hơn về sự khác biệt giữa tốc độ và vận tốc cũng như cách tính toán chúng trong các tình huống thực tế.
XEM THÊM:
6. Kết Luận
Trong quá trình nghiên cứu và phân biệt giữa vận tốc và tốc độ, chúng ta đã nhận thấy một số điểm khác biệt quan trọng. Cả hai khái niệm này đều là những đại lượng cơ bản trong vật lý học, tuy nhiên, chúng có các đặc trưng riêng biệt.
- Đơn vị đo: Tốc độ thường được đo bằng đơn vị khoảng cách trên thời gian như mét trên giây (m/s) hoặc dặm trên giờ (mph), trong khi vận tốc là một vector có đơn vị tương tự nhưng bao gồm cả hướng.
- Tính chất: Tốc độ là một đại lượng vô hướng chỉ có độ lớn, còn vận tốc là một đại lượng vector có cả độ lớn và hướng.
- Biểu diễn: Tốc độ thường được biểu diễn bằng một giá trị duy nhất, trong khi vận tốc được biểu diễn bằng một vector có độ lớn và hướng di chuyển.
- Ứng dụng: Trong thực tiễn, vận tốc được sử dụng để xác định hướng di chuyển của các đối tượng, trong khi tốc độ chỉ quan tâm đến độ nhanh chậm của chuyển động.
Tóm lại, sự hiểu biết về vận tốc và tốc độ không chỉ giúp chúng ta nắm rõ hơn về các khái niệm cơ bản trong vật lý mà còn áp dụng vào nhiều lĩnh vực khác nhau trong cuộc sống hàng ngày và khoa học kỹ thuật.