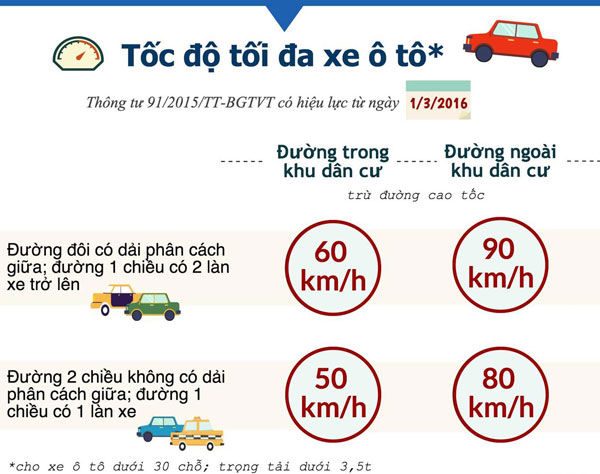
Những Bài Toán Về Vận Tốc, Quãng Đường Thời Gian: Hướng Dẫn Chi Tiết Và Ứng Dụng Thực Tiễn

Bài toán về vận tốc, quãng đường và thời gian là những bài toán cơ bản trong chương trình học phổ thông. Dưới đây là một số ví dụ và công thức liên quan đến chủ đề này.

Công Thức Tính Toán Cơ Bản

• Công thức tính vận tốc: \( v = \dfrac{S}{t} \) trong đó:
  • \( v \): Vận tốc (đơn vị: km/h hoặc m/s)
  • \( S \): Quãng đường (đơn vị: km hoặc m)
  • \( t \): Thời gian (đơn vị: h hoặc s)
• Công thức tính quãng đường: \( S = v \times t \)
• Công thức tính thời gian: \( t = \dfrac{S}{v} \)

Một Số Bài Toán Tiêu Biểu

1. Bài toán 1: Một ô tô đi trong 4 giờ với vận tốc 42,5 km/giờ. Tính quãng đường đi được của ô tô.

   Giải: \( S = 42,5 \times 4 = 170 \, \text{km} \)

2. Bài toán 2: Một ô tô đi quãng đường AB dài 135 km trong 2 giờ 30 phút, dọc đường ô tô nghỉ 15 phút. Tính vận tốc của ô tô.

   Giải: Thời gian đi: 2 giờ 30 phút - 15 phút = 2 giờ 15 phút = 2,25 giờ.

   Vận tốc: \( v = \dfrac{135}{2,25} = 60 \, \text{km/h} \)

3. Bài toán 3: Một ca nô đi với vận tốc 15,2 km/giờ. Tính quãng đường đi được của ca nô trong 3 giờ.

   Giải: \( S = 15,2 \times 3 = 45,6 \, \text{km} \)

4. Bài toán 4: Một người đi xe đạp trong 15 phút với vận tốc 12,6 km/giờ. Tính quãng đường đi được.

   Giải: \( t = \dfrac{15}{60} = 0,25 \, \text{giờ} \)

   Quãng đường: \( S = 12,6 \times 0,25 = 3,15 \, \text{km} \)

Lưu Ý Khi Giải Toán

• Kiểm tra và thống nhất đơn vị đo trước khi thực hiện phép tính.
• Đối với các bài toán liên quan đến hàng hải hoặc thiên văn học, cần sử dụng các đơn vị đo đặc thù như "nút" hoặc "năm ánh sáng".
• Trong bài toán thực tế, cần chú ý đến thời gian nghỉ ngơi và thời gian di chuyển để có kết quả chính xác.

Ứng Dụng Thực Tiễn

Các bài toán về vận tốc, quãng đường và thời gian không chỉ là các bài toán học thuật mà còn có ứng dụng trong đời sống hàng ngày như tính toán lộ trình di chuyển, dự đoán thời gian đến nơi, và nhiều lĩnh vực khác trong khoa học và kỹ thuật.

Trong toán học và vật lý, các bài toán về vận tốc, quãng đường và thời gian là nền tảng quan trọng, không chỉ giúp học sinh nắm vững kiến thức cơ bản mà còn có ứng dụng rộng rãi trong đời sống hàng ngày. Để hiểu rõ hơn về mối quan hệ giữa vận tốc, quãng đường và thời gian, chúng ta cần nắm vững các khái niệm và công thức cơ bản.

• Vận tốc (v): Vận tốc là đại lượng cho biết mức độ nhanh hay chậm của một vật thể khi di chuyển. Công thức tính vận tốc là:

• Trong đó, \( v \) là vận tốc, \( S \) là quãng đường, và \( t \) là thời gian di chuyển.
• Đơn vị đo vận tốc thường là km/h (kilômét trên giờ) hoặc m/s (mét trên giây).

• Quãng đường (S): Quãng đường là độ dài mà vật thể di chuyển được trên một hành trình nhất định. Công thức tính quãng đường là:

• Đơn vị đo quãng đường thường là km (kilômét) hoặc m (mét).

• Thời gian (t): Thời gian là khoảng thời gian mà một vật thể cần để di chuyển hết quãng đường. Công thức tính thời gian là:

• Đơn vị đo thời gian thường là giờ (h), phút (ph), hoặc giây (s).

Các bài toán về vận tốc, quãng đường và thời gian thường yêu cầu chúng ta áp dụng linh hoạt các công thức trên, đồng thời kiểm tra kỹ các đơn vị đo lường để đảm bảo tính toán chính xác. Ngoài ra, những bài toán này còn có thể bao gồm các yếu tố phụ như thời gian nghỉ, thay đổi vận tốc hoặc quãng đường phức tạp, đòi hỏi khả năng phân tích và giải quyết vấn đề một cách có hệ thống.

Các bài toán về vận tốc, quãng đường và thời gian rất đa dạng, từ những bài toán cơ bản đến những bài toán phức tạp yêu cầu khả năng phân tích cao. Việc phân loại các bài toán này giúp học sinh dễ dàng nhận biết và áp dụng đúng phương pháp giải quyết. Dưới đây là các loại bài toán phổ biến.

1. Bài Toán Tính Vận Tốc

Loại bài toán này yêu cầu tính toán vận tốc khi đã biết quãng đường và thời gian di chuyển. Công thức cơ bản được sử dụng là:

• Ví dụ: Một xe ô tô đi được 120 km trong 2 giờ. Tính vận tốc trung bình của xe.
• Giải: \( v = \dfrac{120}{2} = 60 \, \text{km/h} \)

2. Bài Toán Tính Quãng Đường

Bài toán này yêu cầu tính quãng đường đã đi khi biết vận tốc và thời gian di chuyển. Công thức cơ bản là:

• Ví dụ: Một tàu hỏa chạy với vận tốc 50 km/h trong 3 giờ. Tính quãng đường tàu đã đi.
• Giải: \( S = 50 \times 3 = 150 \, \text{km} \)

3. Bài Toán Tính Thời Gian

Loại bài toán này yêu cầu tính thời gian cần thiết để di chuyển một quãng đường nhất định với vận tốc đã cho. Công thức sử dụng là:

• Ví dụ: Một người đi bộ với vận tốc 5 km/h. Tính thời gian để đi hết quãng đường 20 km.
• Giải: \( t = \dfrac{20}{5} = 4 \, \text{giờ} \)

4. Bài Toán Có Yếu Tố Phụ Trợ

Đây là những bài toán phức tạp hơn, bao gồm các yếu tố như thời gian nghỉ, thay đổi vận tốc, hoặc quãng đường không đều. Các bài toán này yêu cầu học sinh phân tích kỹ lưỡng và áp dụng nhiều công thức khác nhau.

• Ví dụ: Một ô tô đi từ A đến B với vận tốc 60 km/h trong 2 giờ đầu, sau đó giảm xuống còn 40 km/h trong 1 giờ tiếp theo. Tính quãng đường từ A đến B.
• Giải: Quãng đường trong 2 giờ đầu: \( S_1 = 60 \times 2 = 120 \, \text{km} \)
• Quãng đường trong 1 giờ sau: \( S_2 = 40 \times 1 = 40 \, \text{km} \)
• Tổng quãng đường từ A đến B: \( S = S_1 + S_2 = 120 + 40 = 160 \, \text{km} \)

Việc nắm vững các loại bài toán này không chỉ giúp học sinh giải nhanh các bài toán vận tốc, quãng đường, thời gian mà còn phát triển khả năng tư duy và phân tích trong nhiều tình huống thực tế.

Giải các bài toán về vận tốc, quãng đường và thời gian đòi hỏi học sinh nắm vững công thức cơ bản và áp dụng chúng một cách linh hoạt. Dưới đây là phương pháp giải từng bước giúp bạn tiếp cận bài toán một cách hiệu quả.

1. Xác Định Yêu Cầu Của Bài Toán

Đầu tiên, hãy đọc kỹ đề bài để xác định rõ yêu cầu của bài toán: cần tính vận tốc, quãng đường hay thời gian? Đồng thời, xác định các dữ kiện đã cho như quãng đường, thời gian, vận tốc, và các yếu tố phụ trợ khác.

2. Lựa Chọn Công Thức Phù Hợp

Dựa vào yêu cầu của bài toán, chọn công thức tương ứng:

• Tính vận tốc: \[ v = \dfrac{S}{t} \]
• Tính quãng đường: \[ S = v \times t \]
• Tính thời gian: \[ t = \dfrac{S}{v} \]

3. Thay Số Vào Công Thức

Sau khi chọn công thức, thay các giá trị số liệu đã biết vào công thức và thực hiện các phép tính. Hãy chắc chắn rằng các đơn vị đo lường đã được chuyển đổi đúng nếu cần thiết.

4. Kiểm Tra Lại Kết Quả

Cuối cùng, kiểm tra lại kết quả để đảm bảo tính hợp lý và chính xác. Nếu cần, hãy so sánh với các tình huống thực tế hoặc dùng phương pháp khác để xác nhận đáp án.

5. Áp Dụng Phương Pháp Giải Nhiều Bước (Nếu Cần)

Đối với các bài toán phức tạp hơn, ví dụ như bài toán có yếu tố thay đổi vận tốc hoặc quãng đường không đều, bạn cần phân chia bài toán thành các bước nhỏ và giải từng bước một. Kết hợp các kết quả từ từng bước để ra kết quả cuối cùng.

Việc nắm vững và thực hành các phương pháp giải trên sẽ giúp bạn tự tin hơn khi đối mặt với các bài toán về vận tốc, quãng đường và thời gian, đồng thời phát triển tư duy logic và khả năng phân tích vấn đề.

Các bài toán về vận tốc, quãng đường và thời gian không chỉ giới hạn trong sách vở mà còn có nhiều ứng dụng thực tế trong cuộc sống. Việc hiểu rõ và áp dụng đúng các công thức này giúp chúng ta giải quyết nhiều vấn đề hàng ngày một cách hiệu quả.

1. Ứng Dụng Trong Giao Thông

Trong lĩnh vực giao thông, việc tính toán vận tốc, quãng đường và thời gian là vô cùng cần thiết. Các ứng dụng cụ thể bao gồm:

• Tính thời gian di chuyển: Trước mỗi chuyến đi, bạn có thể tính toán thời gian cần thiết để đến đích dựa trên quãng đường và vận tốc trung bình của phương tiện. Ví dụ, nếu bạn cần đi quãng đường 120 km với vận tốc trung bình 60 km/h, thời gian dự kiến sẽ là:

• Quy hoạch giao thông: Các nhà quy hoạch sử dụng các bài toán này để thiết kế và cải thiện hệ thống giao thông, đảm bảo sự lưu thông ổn định và an toàn.

2. Ứng Dụng Trong Kinh Doanh Và Logistics

Trong kinh doanh, đặc biệt là lĩnh vực vận tải và logistics, việc tính toán thời gian giao hàng, quãng đường vận chuyển và vận tốc là yếu tố quyết định để tối ưu hóa chi phí và thời gian:

• Tối ưu hóa lộ trình: Dựa trên quãng đường và vận tốc, các doanh nghiệp có thể lựa chọn lộ trình ngắn nhất hoặc hiệu quả nhất cho việc giao hàng, từ đó giảm chi phí và thời gian.
• Quản lý kho bãi: Tính toán thời gian nhập và xuất kho để đảm bảo sản phẩm luôn sẵn sàng theo nhu cầu của khách hàng.

3. Ứng Dụng Trong Thể Thao

Trong thể thao, việc hiểu và áp dụng các bài toán về vận tốc, quãng đường và thời gian giúp vận động viên cải thiện hiệu suất thi đấu:

• Đo lường và cải thiện thành tích: Vận động viên có thể sử dụng công thức tính vận tốc để theo dõi tiến độ và điều chỉnh chiến lược luyện tập, nhằm đạt được thành tích tốt hơn trong các cuộc thi.
• Lên kế hoạch luyện tập: Dựa vào quãng đường và thời gian tập luyện, huấn luyện viên có thể thiết kế các bài tập phù hợp để nâng cao sức bền và tốc độ của vận động viên.

4. Mở Rộng Các Bài Toán Thực Tế

Các bài toán về vận tốc, quãng đường và thời gian cũng có thể được mở rộng để giải quyết các vấn đề phức tạp hơn:

• Bài toán chuyển động tương đối: Khi hai vật thể di chuyển về phía nhau hoặc ngược chiều nhau, việc tính toán thời gian gặp nhau hoặc quãng đường giữa chúng là một ví dụ điển hình.
• Bài toán chuyển động biến đổi: Khi vận tốc thay đổi theo thời gian, chẳng hạn như trong bài toán phanh xe hoặc tăng tốc, các phương pháp phức tạp hơn như tích phân có thể được áp dụng.

Nhờ sự ứng dụng rộng rãi và khả năng mở rộng, các bài toán về vận tốc, quãng đường và thời gian không chỉ là một phần quan trọng trong giáo dục mà còn là công cụ hữu ích trong nhiều lĩnh vực của cuộc sống.