Từ trường Vật lý Đại cương 2: Khái niệm, Định luật và Ứng dụng Thực Tiễn

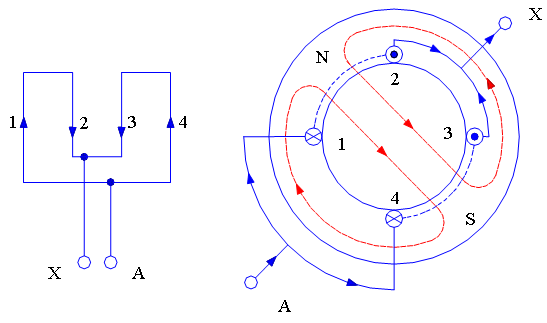
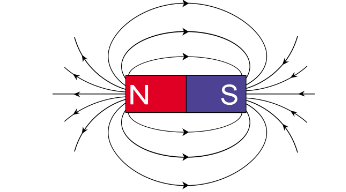
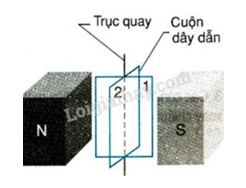
Chủ đề "Từ trường Vật lý Đại cương 2" tập trung vào các kiến thức cơ bản và nâng cao về từ trường trong môn Vật lý, đặc biệt là trong các khóa học đại cương ở bậc đại học. Nội dung này thường bao gồm các khái niệm và định luật liên quan đến từ trường, cách từ trường tương tác với các vật liệu, và ứng dụng của từ trường trong thực tế.

Nội dung chính của "Từ trường Vật lý Đại cương 2"

• Định nghĩa và khái niệm cơ bản về từ trường.
• Các loại từ trường: từ trường tĩnh, từ trường biến thiên.
• Định luật Ampère và ứng dụng trong việc tính toán từ trường xung quanh các dòng điện.
• Định luật Faraday về cảm ứng điện từ và hiện tượng cảm ứng từ.
• Phương trình Maxwell và mô tả thống nhất về điện từ trường.
• Các ứng dụng thực tế của từ trường trong công nghệ và đời sống.

Một số khái niệm và công thức quan trọng

1. Định luật Biot-Savart: Mô tả từ trường tạo bởi một phần tử dòng điện nhỏ. Công thức tổng quát cho từ trường \(\mathbf{B}\) tại một điểm được cho bởi: \[ d\mathbf{B} = \frac{\mu_0}{4\pi} \frac{I \, d\mathbf{l} \times \mathbf{r}}{r^3} \] trong đó \(I\) là cường độ dòng điện, \(d\mathbf{l}\) là vectơ chiều dài phần tử dòng điện, và \(\mathbf{r}\) là vectơ khoảng cách từ phần tử dòng điện đến điểm tính toán.
2. Định luật Ampère: Cho biết từ trường sinh ra quanh một dây dẫn mang dòng điện. Công thức dạng tích phân của định luật này là: \[ \oint_{\partial S} \mathbf{B} \cdot d\mathbf{l} = \mu_0 I_{\text{enc}} \] trong đó \(I_{\text{enc}}\) là tổng dòng điện bao quanh bởi đường cong kín \(\partial S\).
3. Định luật Faraday về cảm ứng điện từ: Miêu tả cách thức mà một từ trường biến thiên theo thời gian có thể sinh ra một điện trường xoáy. Công thức tổng quát là: \[ \mathcal{E} = - \frac{d\Phi_B}{dt} \] trong đó \(\mathcal{E}\) là suất điện động cảm ứng và \(\Phi_B\) là thông lượng từ qua một diện tích xác định.

Ứng dụng của từ trường trong thực tế

• Động cơ điện: Sử dụng từ trường để tạo ra chuyển động quay từ dòng điện.
• Máy phát điện: Chuyển đổi năng lượng cơ học thành năng lượng điện dựa trên nguyên lý cảm ứng từ.
• Các thiết bị điện tử: Từ trường được sử dụng trong hoạt động của các linh kiện điện tử như cuộn cảm, biến áp, và anten.
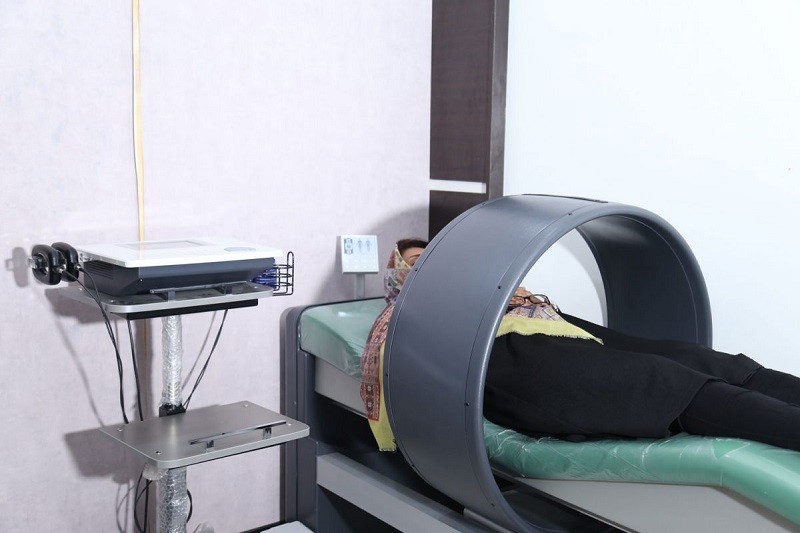
• Y học: Máy MRI (Magnetic Resonance Imaging) sử dụng từ trường mạnh để tạo ra hình ảnh chi tiết của các mô và cơ quan trong cơ thể.

Kết luận

Chủ đề "Từ trường Vật lý Đại cương 2" cung cấp kiến thức cơ bản và cần thiết cho sinh viên ngành Vật lý và Kỹ thuật, giúp họ hiểu rõ hơn về các nguyên lý và ứng dụng của từ trường trong khoa học và công nghệ. Những kiến thức này không chỉ có ý nghĩa học thuật mà còn có giá trị thực tiễn cao trong nhiều lĩnh vực đời sống và công nghiệp.

Từ trường là một trong những khái niệm cơ bản của vật lý học, đặc biệt trong lĩnh vực điện từ học. Từ trường được tạo ra bởi các vật thể mang điện tích di chuyển hoặc bởi các nam châm, và nó ảnh hưởng đến các vật liệu từ tính và các dòng điện trong khu vực xung quanh. Đây là một yếu tố quan trọng trong nhiều hiện tượng vật lý và ứng dụng công nghệ.

Một từ trường có thể được mô tả bằng một vectơ, thường được ký hiệu là \(\mathbf{B}\), thể hiện độ lớn và hướng của từ trường tại mỗi điểm trong không gian. Các đường sức từ được sử dụng để minh họa từ trường, với hướng của các đường này chỉ hướng của lực từ tại mỗi điểm, và mật độ của chúng biểu thị độ lớn của từ trường.

• Định nghĩa từ trường: Từ trường là một trường vectơ đặc trưng bởi từ lực mà nó tác dụng lên các vật liệu từ tính và các hạt mang điện tích đang chuyển động.
• Đơn vị đo: Đơn vị đo của từ trường trong hệ SI là Tesla (T), được định nghĩa là \(1 \, T = 1 \, \text{kg} \cdot \text{s}^{-2} \cdot \text{A}^{-1}\).
• Nguồn gốc của từ trường: Từ trường có thể được tạo ra bởi:
  1. Các nam châm vĩnh cửu.
  2. Dòng điện chạy qua dây dẫn.
  3. Thay đổi trong trường điện từ.
• Các tính chất của từ trường:
  • Từ trường có khả năng tạo ra lực tác dụng lên các vật liệu từ tính và dòng điện.
  • Từ trường có thể được mô tả bởi các đường sức từ, không bao giờ cắt nhau, đi ra từ cực Bắc và đi vào cực Nam của nam châm.
  • Cảm ứng từ tại một điểm là kết quả của sự tổng hợp từ trường từ nhiều nguồn khác nhau.

Hiểu rõ về từ trường và các tính chất của nó giúp chúng ta áp dụng các nguyên lý này vào các ứng dụng thực tế như động cơ điện, máy phát điện, và nhiều công nghệ hiện đại khác. Việc nghiên cứu từ trường không chỉ giúp cải thiện các công nghệ hiện có mà còn mở ra nhiều cơ hội mới trong khoa học và kỹ thuật.

Hiểu rõ các khái niệm cơ bản trong từ trường là nền tảng để nghiên cứu sâu hơn về điện từ học và các ứng dụng thực tế. Dưới đây là một số khái niệm quan trọng trong từ trường:

• Đường sức từ: Đường sức từ là các đường tưởng tượng được sử dụng để biểu diễn từ trường. Chúng chỉ hướng và độ lớn của từ trường tại mỗi điểm. Đường sức từ đi ra từ cực Bắc và đi vào cực Nam của nam châm, và chúng không bao giờ cắt nhau. Độ dày của các đường sức từ biểu thị độ mạnh của từ trường; càng dày, từ trường càng mạnh.
• Từ thông (\(\Phi_B\)): Từ thông là một đại lượng đo lường số lượng đường sức từ đi qua một diện tích cụ thể. Nó được tính toán bằng công thức: \[ \Phi_B = \int_S \mathbf{B} \cdot d\mathbf{A} \] trong đó \(\mathbf{B}\) là cảm ứng từ và \(d\mathbf{A}\) là vectơ diện tích nhỏ trên bề mặt \(S\). Từ thông là một yếu tố quan trọng trong việc hiểu cách từ trường thay đổi và tương tác với các vật liệu khác nhau.
• Cảm ứng từ (\(\mathbf{B}\)): Cảm ứng từ là một đại lượng vectơ biểu thị từ trường tại một điểm trong không gian. Nó thể hiện cả độ lớn và hướng của từ trường. Đơn vị của cảm ứng từ là Tesla (T). Cảm ứng từ được tạo ra bởi dòng điện hoặc bởi các vật liệu có tính chất từ tính.
• Định luật Ampère: Định luật Ampère mô tả mối quan hệ giữa dòng điện và từ trường mà nó tạo ra. Theo định luật Ampère, từ trường xung quanh một dòng điện thẳng tỷ lệ thuận với cường độ dòng điện và tỷ lệ nghịch với khoảng cách từ dòng điện: \[ \oint_{\partial S} \mathbf{B} \cdot d\mathbf{l} = \mu_0 I_{\text{enc}} \] trong đó \(I_{\text{enc}}\) là dòng điện bao quanh đường cong kín \(\partial S\), và \(\mu_0\) là độ từ thẩm của chân không.
• Định luật Faraday về cảm ứng điện từ: Định luật Faraday cho biết sự thay đổi từ thông qua một mạch kín sẽ tạo ra một suất điện động (EMF) trong mạch đó. Công thức của định luật Faraday là: \[ \mathcal{E} = - \frac{d\Phi_B}{dt} \] trong đó \(\mathcal{E}\) là suất điện động cảm ứng và \(\frac{d\Phi_B}{dt}\) là tốc độ thay đổi từ thông. Định luật này là nền tảng cho hoạt động của các thiết bị như máy phát điện và máy biến áp.

Các khái niệm cơ bản này không chỉ giúp chúng ta hiểu rõ hơn về từ trường mà còn đóng vai trò quan trọng trong việc nghiên cứu các hiện tượng điện từ khác và ứng dụng chúng vào công nghệ hiện đại, từ việc thiết kế các động cơ điện, máy phát điện, đến các hệ thống viễn thông và thiết bị y tế như MRI.

Từ trường của dòng điện là một khái niệm quan trọng trong vật lý học, đặc biệt là trong lĩnh vực điện từ học. Dòng điện chạy qua dây dẫn tạo ra từ trường xung quanh nó, và đặc tính của từ trường này phụ thuộc vào hình dạng của dòng điện và cường độ dòng điện.

• Từ trường do dòng điện thẳng:

  Khi dòng điện chạy qua một dây dẫn thẳng, từ trường sinh ra xung quanh dây dẫn đó có dạng các đường tròn đồng tâm, với dây dẫn là tâm. Cảm ứng từ tại một điểm cách dây dẫn một khoảng cách \(r\) được tính bằng công thức:

  \[ B = \frac{\mu_0 I}{2 \pi r} \]

  trong đó \(B\) là cảm ứng từ, \(\mu_0\) là độ từ thẩm của chân không, \(I\) là cường độ dòng điện và \(r\) là khoảng cách từ điểm đến dây dẫn.

• Từ trường do dòng điện tròn:

  Khi dòng điện chạy qua một vòng dây tròn, từ trường sinh ra có dạng phức tạp hơn. Tại tâm của vòng dây, cảm ứng từ được tính bằng công thức:

  \[ B = \frac{\mu_0 I}{2R} \]

  trong đó \(R\) là bán kính của vòng dây. Từ trường tại các điểm khác dọc theo trục vòng dây giảm dần theo khoảng cách từ tâm vòng dây.

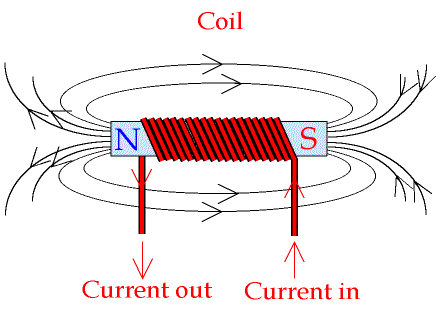
• Từ trường của ống dây (solenoid):

  Một ống dây (solenoid) là một cuộn dây với nhiều vòng dây quấn đều nhau. Khi có dòng điện chạy qua, ống dây tạo ra một từ trường mạnh và đều trong lòng ống, với các đường sức từ song song và rất gần nhau. Cảm ứng từ bên trong một ống dây dài được tính bởi công thức:

  \[ B = \mu_0 n I \]

  trong đó \(n\) là số vòng dây trên một đơn vị chiều dài của ống dây và \(I\) là cường độ dòng điện. Bên ngoài ống dây, từ trường gần như bằng 0.

• Từ trường trong các vật liệu từ:

  Khi đặt dòng điện trong các vật liệu từ tính như sắt hoặc thép, từ trường tạo ra có thể được khuếch đại do tính chất của các vật liệu này. Các vật liệu từ tính này có khả năng làm tăng từ trường do chúng chứa các miền từ tính, và khi chịu tác động của dòng điện, các miền này sắp xếp lại để khuếch đại từ trường tổng thể.

Tóm lại, từ trường do dòng điện tạo ra có nhiều dạng khác nhau tùy thuộc vào hình dạng và cấu trúc của dây dẫn cũng như cường độ dòng điện. Hiểu rõ các khái niệm này giúp chúng ta thiết kế các thiết bị điện và điện tử hiệu quả hơn, từ động cơ điện đến các thiết bị y tế hiện đại.

Từ trường có rất nhiều ứng dụng trong khoa học, công nghệ và đời sống hàng ngày. Dưới đây là một số ứng dụng nổi bật của từ trường:

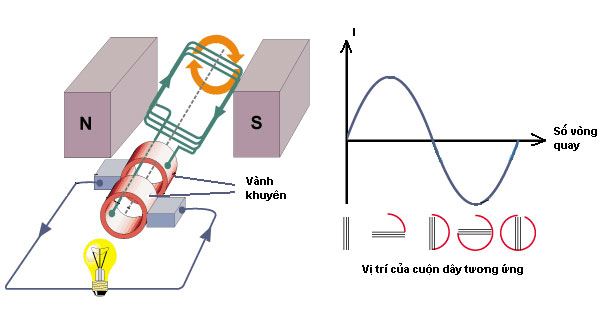
• Động cơ điện và máy phát điện:

  Từ trường đóng vai trò then chốt trong hoạt động của động cơ điện và máy phát điện. Động cơ điện chuyển đổi năng lượng điện thành năng lượng cơ học nhờ từ trường tương tác với dòng điện trong cuộn dây, gây ra chuyển động quay. Ngược lại, máy phát điện tạo ra điện năng bằng cách sử dụng chuyển động cơ học để quay một cuộn dây trong từ trường, tạo ra một suất điện động cảm ứng theo định luật Faraday.

• Cảm biến từ và công nghệ định vị:

  Cảm biến từ sử dụng từ trường để phát hiện sự thay đổi trong vị trí, tốc độ hoặc dòng điện. Các ứng dụng phổ biến bao gồm hệ thống phanh ABS trong ô tô, cảm biến từ cho cửa an ninh, và công nghệ định vị GPS. Các cảm biến Hall, ví dụ, sử dụng hiệu ứng Hall để đo cường độ và hướng của từ trường, giúp xác định vị trí và chuyển động của các đối tượng.

• Thiết bị y tế:

  Từ trường được sử dụng rộng rãi trong y tế, đặc biệt là trong các kỹ thuật hình ảnh y tế như chụp cộng hưởng từ (MRI). MRI sử dụng từ trường mạnh để tạo ra hình ảnh chi tiết của cơ thể, giúp chẩn đoán các vấn đề sức khỏe mà không cần can thiệp phẫu thuật. Ngoài ra, từ trường còn được dùng trong các phương pháp điều trị như trị liệu từ trường để giảm đau và phục hồi chức năng.

• Lưu trữ dữ liệu:

  Các thiết bị lưu trữ dữ liệu từ tính như đĩa cứng (HDD) và băng từ sử dụng từ trường để đọc và ghi dữ liệu. Trong các thiết bị này, dữ liệu được lưu trữ dưới dạng các vùng từ hóa khác nhau trên bề mặt từ tính. Đầu đọc ghi sử dụng từ trường để thay đổi hoặc phát hiện các trạng thái từ hóa, cho phép truy cập và lưu trữ dữ liệu một cách hiệu quả và nhanh chóng.

• Các ứng dụng trong nghiên cứu khoa học:

  Từ trường còn được sử dụng trong nhiều nghiên cứu khoa học và kỹ thuật. Ví dụ, trong vật lý plasma và nghiên cứu nhiệt hạch, từ trường mạnh được dùng để kiểm soát plasma nóng trong các thiết bị như tokamak. Trong nghiên cứu sinh học, từ trường được dùng để định hướng và điều khiển sự di chuyển của các tế bào và phân tử từ tính.

Nhờ các ứng dụng đa dạng và quan trọng, từ trường đóng vai trò thiết yếu trong nhiều lĩnh vực khác nhau, từ công nghệ thông tin và truyền thông, y tế, năng lượng, đến nghiên cứu khoa học. Việc tiếp tục nghiên cứu và phát triển các ứng dụng mới của từ trường hứa hẹn mang lại nhiều lợi ích hơn nữa cho xã hội.

Các phương trình Maxwell là một tập hợp gồm bốn phương trình cơ bản miêu tả sự liên hệ giữa điện trường và từ trường, đồng thời là nền tảng của lý thuyết điện từ trường cổ điển. Các phương trình này được đặt theo tên nhà vật lý James Clerk Maxwell, người đã thống nhất các lý thuyết về điện và từ thành một lý thuyết duy nhất. Các phương trình Maxwell bao gồm:

1. Phương trình Maxwell-Gauss cho điện trường:

   Phương trình này mô tả mối quan hệ giữa điện trường và mật độ điện tích. Nó cho biết rằng điện thông qua một bề mặt kín tỷ lệ với tổng điện tích chứa bên trong bề mặt đó. Phương trình được biểu diễn dưới dạng tích phân và vi phân như sau:

   \[ \oint_{\partial V} \mathbf{E} \cdot d\mathbf{A} = \frac{Q_{\text{enc}}}{\epsilon_0} \]

   hay

   \[ \nabla \cdot \mathbf{E} = \frac{\rho}{\epsilon_0} \]

   trong đó \(\mathbf{E}\) là điện trường, \(\rho\) là mật độ điện tích, và \(\epsilon_0\) là hằng số điện môi của chân không.

2. Phương trình Maxwell-Gauss cho từ trường:

   Phương trình này chỉ ra rằng không tồn tại các đơn cực từ (tức là không có "điểm nguồn" của từ trường giống như điện tích đối với điện trường). Tổng thông lượng từ qua bất kỳ bề mặt kín nào cũng luôn bằng 0. Phương trình được viết dưới dạng:

   \[ \oint_{\partial V} \mathbf{B} \cdot d\mathbf{A} = 0 \]

   hay

   \[ \nabla \cdot \mathbf{B} = 0 \]

   trong đó \(\mathbf{B}\) là cảm ứng từ.

3. Phương trình Faraday về cảm ứng điện từ:

   Phương trình này miêu tả sự thay đổi của từ thông qua một vòng dây dẫn tạo ra một suất điện động trong dây dẫn đó. Đây là nguyên lý cơ bản đằng sau máy phát điện, máy biến áp, và nhiều thiết bị khác. Phương trình được viết như sau:

   \[ \oint_{\partial S} \mathbf{E} \cdot d\mathbf{l} = - \frac{d\Phi_B}{dt} \]

   hay

   \[ \nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t} \]

   trong đó \(\Phi_B\) là từ thông qua bề mặt \(S\).

4. Phương trình Ampère-Maxwell:

   Phương trình này mở rộng định luật Ampère bằng cách thêm một thành phần liên quan đến sự thay đổi của điện trường theo thời gian, gọi là dòng dịch chuyển. Phương trình này cho thấy mối liên hệ giữa từ trường và dòng điện, cũng như sự thay đổi của điện trường theo thời gian:

   \[ \oint_{\partial S} \mathbf{B} \cdot d\mathbf{l} = \mu_0 \left( I_{\text{enc}} + \epsilon_0 \frac{d\Phi_E}{dt} \right) \]

   hay

   \[ \nabla \times \mathbf{B} = \mu_0 \mathbf{J} + \mu_0 \epsilon_0 \frac{\partial \mathbf{E}}{\partial t} \]

   trong đó \(I_{\text{enc}}\) là dòng điện qua bề mặt \(S\), và \(\Phi_E\) là thông điện.

Các phương trình Maxwell không chỉ mô tả cách điện trường và từ trường tương tác mà còn dự đoán sự tồn tại của sóng điện từ, một loại sóng mà ánh sáng là một ví dụ cụ thể. Sóng điện từ lan truyền trong không gian với tốc độ của ánh sáng, và đặc tính này là nền tảng cho nhiều công nghệ hiện đại như truyền thông không dây, radar, và viễn thám.

Tổng kết, các phương trình Maxwell đã cung cấp một khung lý thuyết vững chắc cho nghiên cứu về điện từ trường và đã mở đường cho nhiều khám phá khoa học và ứng dụng công nghệ sau này. Hiểu rõ các phương trình này giúp chúng ta áp dụng các nguyên lý điện từ vào việc thiết kế và vận hành các hệ thống kỹ thuật và khoa học phức tạp.

Trong phần này, chúng ta sẽ đi qua một số bài tập và ví dụ minh họa nhằm củng cố các kiến thức đã học về từ trường. Các bài tập được chia theo từng chủ đề để bạn dễ dàng ôn tập và nắm vững các khái niệm cơ bản cũng như các định luật quan trọng trong phần từ trường của Vật lý Đại cương 2.

6.1 Bài tập về định luật Ampère

1. Bài tập 1: Tính từ trường tại một điểm cách dây dẫn thẳng dài vô hạn một khoảng \( r \) khi dây dẫn này mang dòng điện \( I \). Sử dụng định luật Ampère để giải bài toán.

   Hướng dẫn:

   • Sử dụng định luật Ampère: \(\oint \mathbf{B} \cdot d\mathbf{l} = \mu_0 I_{\text{enc}}\)
   • Do đối xứng của vấn đề, từ trường \( \mathbf{B} \) tại khoảng cách \( r \) là không đổi theo chu vi vòng tròn có bán kính \( r \), ta có: \(\mathbf{B} \cdot 2\pi r = \mu_0 I\)
   • Giải ra: \(\mathbf{B} = \frac{\mu_0 I}{2\pi r}\)

2. Bài tập 2: Tính từ thông xuyên qua một vòng dây tròn có bán kính \( R \) đặt trong một từ trường đều có cường độ \( B \) vuông góc với mặt phẳng vòng dây.

   Hướng dẫn:

   • Từ thông: \(\Phi = \int \mathbf{B} \cdot d\mathbf{A}\)
   • Vì \( \mathbf{B} \) vuông góc với mặt phẳng vòng dây nên \( \mathbf{B} \cdot d\mathbf{A} = B \cdot dA \)
   • Từ thông qua vòng dây: \(\Phi = B \cdot \pi R^2\)

6.2 Bài tập về định luật Faraday

1. Bài tập 1: Một vòng dây tròn có diện tích \( A \) và 10 vòng dây được đặt trong từ trường đều. Nếu từ thông qua vòng dây thay đổi từ \( \Phi_1 \) đến \( \Phi_2 \) trong thời gian \( \Delta t \), hãy tính suất điện động cảm ứng trong vòng dây.

   Hướng dẫn:

   • Sử dụng định luật Faraday: \(\mathcal{E} = -\frac{d\Phi}{dt}\)
   • Suất điện động cảm ứng: \(\mathcal{E} = -N \frac{\Phi_2 - \Phi_1}{\Delta t}\)

2. Bài tập 2: Một dây dẫn dạng hình chữ nhật di chuyển với vận tốc \( v \) trong từ trường đều \( \mathbf{B} \) vuông góc với mặt phẳng chứa dây. Tính suất điện động cảm ứng trong dây dẫn.

   Hướng dẫn:

   • Sử dụng công thức: \(\mathcal{E} = Bvl\) (với \( l \) là chiều dài của dây dẫn).

6.3 Bài tập tổng hợp về từ trường

1. Bài tập 1: Một ống dây dài \( l \) có \( N \) vòng dây mang dòng điện \( I \). Hãy tính từ trường bên trong ống dây.

   Hướng dẫn:

   • Sử dụng định luật Ampère trong trường hợp ống dây dài:
   • Từ trường bên trong ống dây: \( \mathbf{B} = \mu_0 \frac{N}{l} I \)

2. Bài tập 2: Một vòng dây tròn có diện tích \( A \) được quay với vận tốc góc \( \omega \) trong từ trường đều \( B \). Tính suất điện động cảm ứng xuất hiện trong vòng dây theo thời gian.

   Hướng dẫn:

   • Sử dụng công thức: \(\mathcal{E} = -\frac{d\Phi}{dt} = -\frac{d}{dt} (B \cdot A \cdot \cos(\omega t))\)
   • Kết quả: \( \mathcal{E} = B \cdot A \cdot \omega \cdot \sin(\omega t)\)

Trong bài học về từ trường của Vật lý Đại cương 2, chúng ta đã khám phá các khái niệm cơ bản như từ thông, định luật Faraday, và định luật Ampère, cũng như các ứng dụng quan trọng của từ trường trong công nghệ và đời sống. Những kiến thức này không chỉ giúp hiểu sâu hơn về thế giới vật lý mà còn mở ra nhiều hướng phát triển công nghệ trong tương lai.

7.1 Tóm tắt các khái niệm chính

• Từ trường: Là một dạng năng lượng có thể tác động lên các hạt mang điện, dòng điện, và các vật liệu từ.
• Định luật Faraday: Định nghĩa về sự cảm ứng điện từ, một hiện tượng cơ bản trong các thiết bị điện như máy phát điện và động cơ.
• Định luật Ampère: Mô tả mối quan hệ giữa từ trường và dòng điện, tạo nền tảng cho việc tính toán và thiết kế các mạch điện.

7.2 Hướng nghiên cứu và ứng dụng mới trong từ trường

Trong tương lai, nghiên cứu về từ trường sẽ tiếp tục mở rộng và có thể dẫn đến các đột phá lớn trong nhiều lĩnh vực:

1. Năng lượng tái tạo: Phát triển các máy phát điện hiệu suất cao và động cơ từ trường vĩnh cửu, góp phần giảm thiểu sự phụ thuộc vào nhiên liệu hóa thạch.
2. Y học: Ứng dụng từ trường trong công nghệ hình ảnh như MRI và các phương pháp điều trị không xâm lấn, mở ra kỷ nguyên mới cho y học hiện đại.
3. Công nghệ vật liệu: Khám phá các vật liệu từ mới với tính năng vượt trội, hỗ trợ sự phát triển của điện tử và công nghệ thông tin.
4. Truyền thông và điện tử: Nghiên cứu về siêu vật liệu và từ trường trong các thiết bị viễn thông, có thể cải thiện tốc độ và độ tin cậy của mạng lưới truyền thông.

Tóm lại, từ trường không chỉ là một phần cốt lõi của vật lý học mà còn là động lực thúc đẩy nhiều ngành công nghiệp và nghiên cứu khoa học tiên tiến. Với sự phát triển của công nghệ và sự hiểu biết ngày càng sâu rộng, chắc chắn từ trường sẽ tiếp tục mang lại nhiều ứng dụng mới mẻ và đầy tiềm năng.