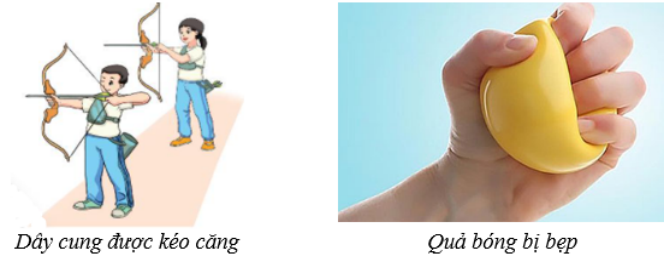
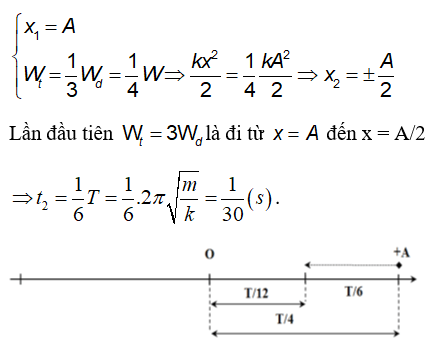Chủ đề thế năng đơn vị: Thế năng đơn vị là một khái niệm quan trọng trong vật lý, được sử dụng để đo lường năng lượng tiềm tàng của một vật thể trong một hệ thống. Đơn vị đo lường thế năng là Joule (J), và khái niệm này áp dụng rộng rãi trong các lĩnh vực như khoa học, kỹ thuật và công nghệ. Bài viết này sẽ giúp bạn hiểu rõ hơn về khái niệm, công thức tính toán, và ứng dụng của thế năng đơn vị trong thực tế.
Mục lục
Thế Năng Đơn Vị
Thế năng là một khái niệm quan trọng trong vật lý, được sử dụng để chỉ năng lượng tiềm tàng của một vật khi nó ở một vị trí nhất định trong một trường lực. Các đơn vị phổ biến của thế năng bao gồm Joule (J), một đơn vị đo năng lượng trong hệ thống quốc tế SI.
Các Dạng Thế Năng
- Thế Năng Trọng Trường: Thế năng này liên quan đến vị trí của một vật trong trường trọng lực. Công thức tính toán như sau:
- \( W \): Thế năng trọng trường (J)
- \( m \): Khối lượng của vật (kg)
- \( g \): Gia tốc trọng trường (\( m/s^2 \))
- \( h \): Độ cao của vật so với mốc chuẩn (m)
- Thế Năng Đàn Hồi: Năng lượng tiềm tàng của một vật khi nó bị biến dạng đàn hồi (ví dụ: kéo dãn hoặc nén lò xo). Công thức tính toán:
- \( U \): Thế năng đàn hồi (J)
- \( k \): Hệ số đàn hồi của lò xo (\( N/m \))
- \( x \): Độ biến dạng của lò xo (m)
- Thế Năng Điện Trường: Năng lượng tiềm tàng của một điện tích do vị trí của nó trong điện trường. Công thức tính toán:
- \( U \): Thế năng điện trường (J)
- \( k \): Hằng số Coulomb (\( \approx 8.99 \times 10^9 Nm^2/C^2 \))
- \( q_1, q_2 \): Các điện tích (C)
- \( r \): Khoảng cách giữa các điện tích (m)
\[ W = m \cdot g \cdot h \]
Trong đó:
\[ U = \frac{1}{2} k x^2 \]
Trong đó:
\[ U = k \frac{q_1 q_2}{r} \]
Trong đó:
Ví Dụ Về Thế Năng
Dưới đây là một ví dụ cụ thể về cách tính thế năng trọng trường:
- Giả sử một quả bóng có khối lượng 2 kg được nâng lên độ cao 5 m trong một trường trọng lực với gia tốc \( g = 9.8 \, m/s^2 \). Thế năng trọng trường của quả bóng được tính như sau:
- Vì vậy, thế năng trọng trường của quả bóng tại độ cao 5 m là 98 Joules.
\[ W = 2 \cdot 9.8 \cdot 5 = 98 \, J \]
Ứng Dụng Của Thế Năng
Thế năng có vai trò quan trọng trong nhiều lĩnh vực khoa học và kỹ thuật, từ việc tính toán năng lượng cần thiết để di chuyển vật thể đến việc phát triển các hệ thống năng lượng tái tạo.
Kết Luận
Thế năng và các đơn vị đo của nó là nền tảng cho việc hiểu và ứng dụng năng lượng trong nhiều khía cạnh của cuộc sống và kỹ thuật. Từ thế năng trọng trường đến thế năng điện trường và thế năng đàn hồi, mỗi loại đều có những ứng dụng cụ thể, giúp chúng ta hiểu rõ hơn về cách năng lượng được lưu trữ và chuyển đổi trong tự nhiên.

.png)
I. Giới Thiệu Về Thế Năng
Thế năng là một dạng năng lượng tiềm tàng mà một vật thể sở hữu do vị trí của nó trong một trường lực, thường là trường trọng lực. Khái niệm thế năng được sử dụng rộng rãi trong vật lý để mô tả khả năng sinh công của một vật thể dựa trên vị trí của nó so với các vật thể khác.
Công thức cơ bản để tính thế năng trong trường hợp đơn giản là:
\[
W_t = m \cdot g \cdot h
\]
Trong đó:
- \(W_t\): Thế năng (Joule)
- \(m\): Khối lượng của vật (kg)
- \(g\): Gia tốc trọng trường (m/s²)
- \(h\): Độ cao của vật so với mốc chọn (m)
Thế năng có thể được tính toán không chỉ trong các trường hợp liên quan đến trọng lực mà còn trong các hệ thống khác như lò xo nén, điện trường và từ trường. Công thức tính thế năng sẽ thay đổi tùy thuộc vào trường hợp cụ thể, nhưng ý tưởng chính vẫn là năng lượng tiềm tàng do vị trí của vật trong một trường lực.
II. Công Thức Tính Thế Năng
Thế năng của một vật thể trong một trường lực được xác định dựa trên vị trí của nó trong trường đó. Trong trường hợp phổ biến nhất là trọng trường, công thức tính thế năng trọng trường được xác định như sau:
\[
W_t = m \cdot g \cdot h
\]
Trong đó:
- \(W_t\): Thế năng (Joule)
- \(m\): Khối lượng của vật (kg)
- \(g\): Gia tốc trọng trường, thường lấy giá trị xấp xỉ là 9,8 m/s²
- \(h\): Độ cao của vật so với mốc chọn (m)
Ví dụ, nếu một vật có khối lượng 2 kg được đặt ở độ cao 5 mét so với mặt đất, thì thế năng của vật có thể được tính như sau:
\[
W_t = 2 \cdot 9,8 \cdot 5 = 98 \text{ Joules}
\]
Đối với các hệ thống khác như lò xo hoặc điện trường, công thức tính thế năng sẽ khác nhau, nhưng đều dựa trên nguyên tắc xác định năng lượng tiềm tàng dựa trên vị trí của vật thể trong một trường lực cụ thể.

III. Đơn Vị Đo Thế Năng
Thế năng là một dạng năng lượng tiềm tàng mà một vật sở hữu do vị trí của nó trong một trường lực hoặc cấu trúc bên trong. Đơn vị đo lường thế năng trong Hệ đo lường quốc tế (SI) là Joule (J). Đơn vị này được đặt theo tên của nhà vật lý người Anh James Prescott Joule, người đã có những đóng góp quan trọng trong việc nghiên cứu năng lượng.
1. Joule (J) – Đơn Vị Cơ Bản
Trong hệ SI, Joule là đơn vị chuẩn để đo thế năng. Một Joule được định nghĩa là công thực hiện khi một lực một Newton (N) di chuyển một vật một mét (m) theo hướng của lực. Công thức tính thế năng trọng trường, một trong những dạng phổ biến nhất của thế năng, được biểu diễn như sau:
\[
W_t = m \cdot g \cdot h
\]
- W_t: Thế năng trọng trường (đơn vị: Joule, J)
- m: Khối lượng của vật (đơn vị: kilogram, kg)
- g: Gia tốc trọng trường (đơn vị: mét trên giây bình phương, m/s²)
- h: Độ cao của vật so với mốc tham chiếu (đơn vị: mét, m)
2. Quy Đổi Đơn Vị Thế Năng
Trong một số trường hợp, thế năng có thể được quy đổi sang các đơn vị khác tùy thuộc vào lĩnh vực ứng dụng. Một số đơn vị phổ biến bao gồm:
- Erg: Đơn vị đo trong hệ CGS. 1 Joule = 107 Erg.
- Calorie (cal): Đơn vị năng lượng thường dùng trong nhiệt động học. 1 Joule = 0.239 cal.
- Electronvolt (eV): Đơn vị năng lượng dùng trong vật lý hạt. 1 Joule = 6.242 x 1018 eV.
Bảng Chuyển Đổi Các Đơn Vị Thế Năng
| Đơn Vị | Giá Trị Tương Đương (J) |
|---|---|
| 1 Erg | 10-7 J |
| 1 Calorie (cal) | 4.184 J |
| 1 Electronvolt (eV) | 1.602 x 10-19 J |
Việc hiểu rõ các đơn vị của thế năng và cách chuyển đổi giữa chúng giúp chúng ta dễ dàng ứng dụng các khái niệm này trong nhiều lĩnh vực khác nhau như cơ học, điện học và nhiệt động học.

IV. Ví Dụ Minh Họa và Ứng Dụng
1. Ví Dụ Thế Năng Hấp Dẫn
Thế năng hấp dẫn của một vật thể phụ thuộc vào khối lượng của vật, độ cao so với mốc thế năng và gia tốc trọng trường. Công thức tính thế năng hấp dẫn được biểu diễn như sau:
\[
W_t = m \cdot g \cdot h
\]
Trong đó:
- \(W_t\): Thế năng hấp dẫn (Joules)
- \(m\): Khối lượng của vật (kg)
- \(g\): Gia tốc trọng trường (m/s²)
- \(h\): Độ cao so với mốc thế năng (m)
Ví dụ: Một viên đá có khối lượng 2 kg được nâng lên độ cao 10 m so với mặt đất. Thế năng hấp dẫn của viên đá được tính như sau:
\[
W_t = 2 \cdot 9.8 \cdot 10 = 196 \text{ J}
\]
2. Ví Dụ Thế Năng Đàn Hồi
Thế năng đàn hồi phát sinh khi một lò xo hoặc vật đàn hồi bị biến dạng. Công thức tính thế năng đàn hồi là:
\[
W_{đh} = \frac{1}{2} k x^2
\]
Trong đó:
- \(W_{đh}\): Thế năng đàn hồi (Joules)
- \(k\): Hệ số đàn hồi của lò xo (N/m)
- \(x\): Độ biến dạng của lò xo (m)
Ví dụ: Một lò xo có hệ số đàn hồi \(k = 100 N/m\) bị nén một đoạn 0,2 m. Thế năng đàn hồi của lò xo là:
\[
W_{đh} = \frac{1}{2} \cdot 100 \cdot (0,2)^2 = 2 \text{ J}
\]
3. Ứng Dụng Thế Năng Trong Thực Tiễn
Thế năng được ứng dụng rộng rãi trong đời sống và công nghệ, bao gồm:
- Thủy điện: Sử dụng thế năng của nước trong các đập thủy điện để chuyển hóa thành điện năng, cung cấp điện cho các hoạt động sinh hoạt và sản xuất.
- Lưu trữ năng lượng: Các hệ thống lưu trữ nước bơm sử dụng thế năng để phát điện khi cần thiết.
- Công nghệ vũ trụ: Thế năng giúp duy trì quỹ đạo của vệ tinh và tàu vũ trụ, hỗ trợ các hành trình dài trong không gian.
- Giải trí và thể thao: Thế năng được khai thác trong các trò chơi cảm giác mạnh như tàu lượn siêu tốc và nhảy dù, tạo ra trải nghiệm thú vị cho người tham gia.

V. Bài Tập Thực Hành
Dưới đây là một số bài tập thực hành giúp củng cố kiến thức về thế năng. Các bài tập này sẽ bao gồm việc tính toán thế năng trong các tình huống khác nhau như thế năng trọng trường và thế năng đàn hồi.
1. Bài Tập Tính Thế Năng Trọng Trường
-
Bài Tập 1: Một vật có khối lượng \( m = 2 \, \text{kg} \) được nâng lên độ cao \( h = 5 \, \text{m} \) so với mặt đất. Tính thế năng trọng trường của vật. Lấy gia tốc trọng trường \( g = 9,8 \, \text{m/s}^2 \).
Lời giải: Thế năng trọng trường được tính bằng công thức:
\[ W_t = mgh = 2 \times 9.8 \times 5 = 98 \, \text{J} \]
-
Bài Tập 2: Một vật có khối lượng \( m = 1 \, \text{kg} \) được thả rơi tự do từ độ cao \( h = 10 \, \text{m} \). Bỏ qua sức cản không khí. Tính vận tốc của vật khi chạm đất.
Lời giải: Vận tốc của vật khi chạm đất được tính bằng công thức:
\[ v = \sqrt{2gh} = \sqrt{2 \times 9.8 \times 10} \approx 14 \, \text{m/s} \]
-
Bài Tập 3: Một quả bóng có khối lượng \( m = 0.5 \, \text{kg} \) được ném thẳng đứng lên cao với vận tốc ban đầu \( v_0 = 10 \, \text{m/s} \). Tính độ cao cực đại mà quả bóng đạt được.
Lời giải: Độ cao cực đại được tính bằng công thức:
\[ h_{\text{max}} = \frac{v_0^2}{2g} = \frac{10^2}{2 \times 9.8} \approx 5.1 \, \text{m} \]
2. Bài Tập Tính Thế Năng Đàn Hồi
-
Bài Tập 1: Một lò xo có độ cứng \( k = 100 \, \text{N/m} \) được nén một đoạn \( x = 0.1 \, \text{m} \). Tính thế năng đàn hồi của lò xo.
Lời giải: Thế năng đàn hồi của lò xo được tính bằng công thức:
\[ W_{\text{đàn hồi}} = \frac{1}{2}kx^2 = \frac{1}{2} \times 100 \times (0.1)^2 = 0.5 \, \text{J} \]
-
Bài Tập 2: Một lò xo có độ cứng \( k = 200 \, \text{N/m} \) được kéo giãn một đoạn \( x = 0.2 \, \text{m} \). Tính thế năng đàn hồi của lò xo.
Lời giải: Thế năng đàn hồi của lò xo được tính bằng công thức:
\[ W_{\text{đàn hồi}} = \frac{1}{2}kx^2 = \frac{1}{2} \times 200 \times (0.2)^2 = 4 \, \text{J} \]
XEM THÊM:
VI. Tổng Kết
Thế năng là một khái niệm quan trọng trong vật lý, không chỉ giúp chúng ta hiểu rõ hơn về năng lượng mà còn là nền tảng cho nhiều nguyên lý và ứng dụng trong thực tiễn.
1. Tầm Quan Trọng Của Thế Năng Trong Vật Lý
Thế năng đóng vai trò quan trọng trong nhiều hiện tượng vật lý và kỹ thuật. Nó là cơ sở để giải thích các hiện tượng như chuyển động của các hành tinh, dao động của lò xo, và sự ổn định của cấu trúc tĩnh điện. Hiểu biết về thế năng giúp chúng ta dự đoán và kiểm soát các hiện tượng tự nhiên một cách hiệu quả.
- Thế năng hấp dẫn: Giải thích các hiện tượng như sự rơi tự do, chuyển động của các vệ tinh xung quanh Trái Đất, và cả sự hình thành và tồn tại của các hố đen.
- Thế năng đàn hồi: Đóng vai trò quan trọng trong việc thiết kế các hệ thống lò xo, các cơ cấu dao động trong kỹ thuật.
- Thế năng tĩnh điện: Ứng dụng trong việc thiết kế các tụ điện, hiểu rõ về tương tác giữa các điện tích, và phân tích các trường tĩnh điện.
2. Định Hướng Nghiên Cứu Thêm Về Thế Năng
Để nắm vững hơn về khái niệm thế năng, việc nghiên cứu thêm về các ứng dụng thực tiễn và các bài toán thực hành là cần thiết. Học sinh và sinh viên có thể tìm hiểu thêm qua các tài liệu chuyên sâu, tham gia các dự án nghiên cứu hoặc thực hành các bài tập phức tạp hơn để áp dụng kiến thức đã học vào thực tế.
- Nghiên cứu sâu hơn về thế năng hấp dẫn trong các hệ thiên văn và ứng dụng trong kỹ thuật hàng không vũ trụ.
- Phát triển các bài toán ứng dụng liên quan đến thế năng đàn hồi trong các hệ cơ học phức tạp.
- Khám phá các ứng dụng tiên tiến của thế năng tĩnh điện trong công nghệ nano và điện tử.
Tổng kết lại, thế năng không chỉ là một khái niệm lý thuyết mà còn là một công cụ mạnh mẽ giúp chúng ta hiểu và ứng dụng các nguyên lý vật lý vào cuộc sống. Việc nắm vững và tiếp tục nghiên cứu về thế năng sẽ mở ra nhiều cơ hội trong học tập và nghiên cứu khoa học.