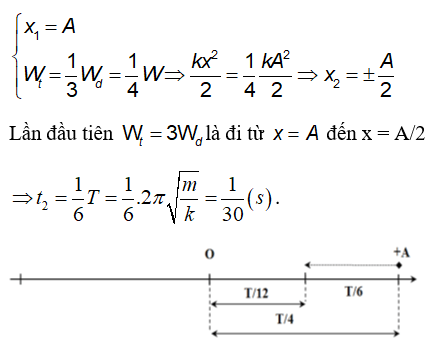Chủ đề thế năng biến thiên với chu kì: Thế năng biến thiên với chu kì là một khái niệm quan trọng trong dao động điều hòa, giúp chúng ta hiểu rõ mối quan hệ giữa chu kì và sự biến đổi năng lượng của vật. Bài viết này sẽ cung cấp cái nhìn chi tiết và trực quan về sự biến thiên của thế năng, từ lý thuyết cơ bản đến ứng dụng trong thực tế.
Mục lục
Thế năng biến thiên với chu kì
Trong vật lý, thế năng và chu kì là hai khái niệm cơ bản đặc biệt quan trọng trong các bài toán về dao động điều hòa. Khi vật dao động, thế năng của nó sẽ biến thiên theo chu kì cụ thể, ảnh hưởng bởi các yếu tố như biên độ, tần số và pha của dao động.
1. Thế năng trong dao động điều hòa
Thế năng là năng lượng mà vật có được do vị trí của nó trong một trường lực. Công thức tính thế năng dao động điều hòa là:
\[ W_t = \frac{1}{2} k x^2 \]
Trong đó:
- k là hằng số lực.
- x là li độ tức thời của vật.
Thế năng của vật dao động điều hòa biến đổi tuần hoàn theo thời gian với tần số gấp đôi tần số dao động của vật.
2. Chu kì và tần số của thế năng
Chu kì của thế năng là khoảng thời gian để thế năng lặp lại giá trị ban đầu. Trong dao động điều hòa, chu kì của thế năng bằng một nửa chu kì dao động của vật, tức là:
\[ T_{thế năng} = \frac{T}{2} \]
Tần số của thế năng gấp đôi tần số của dao động, với công thức:
\[ f_{thế năng} = 2f \]
3. Ứng dụng và ví dụ minh họa
Trong một số bài toán cụ thể, ta có thể xác định được sự biến thiên của thế năng theo chu kì thông qua bảng giá trị như sau:
| Thời điểm | Thế năng |
|---|---|
| t = 0 | \( W_t = \frac{1}{2} k A^2 \) |
| t = \(\frac{T}{4}\) | 0 |
| t = \(\frac{T}{2}\) | \( W_t = \frac{1}{2} k A^2 \) |
| t = \(\frac{3T}{4}\) | 0 |
| t = T | \( W_t = \frac{1}{2} k A^2 \) |
Sự biến thiên này có tính tuần hoàn với chu kì T/2, cho thấy sự lặp lại của giá trị thế năng qua mỗi nửa chu kì dao động.
4. Kết luận
Hiểu rõ về sự biến thiên của thế năng giúp giải quyết tốt các bài toán về dao động điều hòa, ứng dụng trong việc tính toán các bài toán cơ bản đến nâng cao trong vật lý, cũng như trong các lĩnh vực kỹ thuật liên quan.

.png)
1. Khái niệm cơ bản về thế năng và chu kì trong dao động điều hòa
Trong dao động điều hòa, thế năng và chu kì là hai khái niệm quan trọng. Thế năng (Wt) là dạng năng lượng liên quan đến vị trí của vật so với vị trí cân bằng. Khi vật dao động, thế năng của nó biến đổi theo thời gian, đồng thời phụ thuộc vào vị trí và biên độ dao động.
Chu kì (T) là khoảng thời gian để vật hoàn thành một dao động toàn phần. Trong một chu kì dao động, thế năng và động năng liên tục chuyển hóa lẫn nhau. Thế năng đạt giá trị cực đại tại vị trí biên và bằng 0 tại vị trí cân bằng.
Công thức tính thế năng trong dao động điều hòa:
\[
W_t = \dfrac{1}{2} k x^2 = \dfrac{1}{2} k A^2 \cos^2(\omega t + \varphi)
\]
Trong đó:
- k: hằng số lực đàn hồi (N/m).
- x: độ lệch vị trí của vật so với vị trí cân bằng (m).
- A: biên độ dao động (m).
- \(\omega\): tần số góc của dao động (\(\text{rad/s}\)).
- \(\varphi\): pha ban đầu của dao động.
Chu kì T của dao động được xác định bằng công thức:
\[
T = \dfrac{2\pi}{\omega}
\]
Trong quá trình dao động, thế năng biến đổi với tần số gấp đôi tần số của dao động, nghĩa là tần số biến đổi của thế năng là \(2f\), với chu kì bằng \(\dfrac{T}{2}\). Sự biến thiên này thể hiện qua đồ thị có hình dạng tuần hoàn với chu kì nửa so với chu kì dao động toàn phần.
2. Chu kì biến thiên của thế năng trong dao động điều hòa
Trong dao động điều hòa, thế năng của vật biến thiên tuần hoàn với chu kì bằng một nửa chu kì dao động của vật. Khi xét một vật như con lắc lò xo hay con lắc đơn, sự biến đổi thế năng diễn ra theo quy luật sin hoặc cos.
Một cách cụ thể, thế năng đạt giá trị cực đại tại các vị trí biên, nơi vận tốc của vật bằng 0. Tại đây, toàn bộ năng lượng của vật là thế năng. Trong khi đó, tại vị trí cân bằng, thế năng bằng 0 và toàn bộ năng lượng chuyển hóa thành động năng. Chu kì biến đổi thế năng diễn ra đều đặn với tần số gấp đôi tần số dao động của vật.
Vì thế năng biến thiên tuần hoàn nên sự thay đổi của nó trong mỗi chu kì dao động có dạng:
- Khi vật di chuyển từ vị trí biên về vị trí cân bằng: Thế năng giảm dần, động năng tăng dần.
- Khi vật di chuyển từ vị trí cân bằng ra biên: Thế năng tăng dần, động năng giảm dần.
Như vậy, trong mỗi chu kì dao động, có hai thời điểm thế năng và động năng bằng nhau, và mỗi lần này xảy ra tại 1/4 và 3/4 chu kì dao động.

3. So sánh chu kì của thế năng và động năng
Trong dao động điều hòa, thế năng và động năng của vật có mối liên hệ chặt chẽ và biến thiên tuần hoàn theo thời gian. Tuy nhiên, chu kì biến thiên của chúng khác với chu kì dao động của vật.
- Thế năng và động năng biến thiên với tần số gấp đôi tần số dao động của vật, do đó chu kì của chúng là
\(\frac{T}{2}\) , với T là chu kì của dao động điều hòa. - Khi vật đạt vị trí biên, động năng bằng 0 và thế năng đạt giá trị cực đại. Ngược lại, tại vị trí cân bằng, thế năng bằng 0 và động năng cực đại.
- Trong mỗi chu kì dao động của vật, thế năng và động năng sẽ hoán đổi vị trí cực đại hai lần, do đó chu kì biến thiên của chúng chỉ bằng một nửa chu kì dao động.
Việc hiểu rõ chu kì biến thiên của thế năng và động năng giúp dễ dàng phân tích và dự đoán năng lượng tại từng thời điểm trong quá trình dao động điều hòa.

4. Ứng dụng của chu kì biến thiên thế năng trong thực tiễn
Chu kì biến thiên thế năng có vai trò quan trọng trong nhiều lĩnh vực thực tiễn, từ cơ học, kỹ thuật đến đời sống hàng ngày. Trong cơ học, các nguyên tắc này giúp tính toán chính xác công việc và năng lượng cần thiết cho các hệ thống máy móc. Đặc biệt, trong kỹ thuật xây dựng, hiểu rõ sự biến thiên thế năng giúp đảm bảo tính an toàn và ổn định cho các công trình như cầu đường và nhà cao tầng.
Bên cạnh đó, chu kì biến thiên thế năng còn được áp dụng trong nghiên cứu khoa học tự nhiên, như việc phân tích dòng chảy của nước hoặc dự đoán các hiện tượng môi trường. Ngành giải trí cũng không đứng ngoài ứng dụng này, điển hình là trong thiết kế các trò chơi cảm giác mạnh như tàu lượn siêu tốc, nơi việc kiểm soát chính xác năng lượng tiềm năng và động năng là vô cùng quan trọng.
Việc hiểu rõ chu kì biến thiên thế năng còn giúp nâng cao hiệu suất trong các lĩnh vực như y học, qua đó hỗ trợ thiết kế các thiết bị hỗ trợ vận động, hoặc trong công nghệ sản xuất máy móc công nghiệp, đảm bảo tiết kiệm năng lượng và tối ưu hiệu quả hoạt động.