Chủ đề số bội giác của kính hiển vi: Số bội giác của kính hiển vi là một yếu tố quan trọng trong việc hiểu và sử dụng thiết bị này. Bài viết này sẽ cung cấp cho bạn cái nhìn tổng quan về cách tính toán, ứng dụng, và những kiến thức hữu ích khác liên quan đến số bội giác của kính hiển vi.
Mục lục
Số Bội Giác Của Kính Hiển Vi
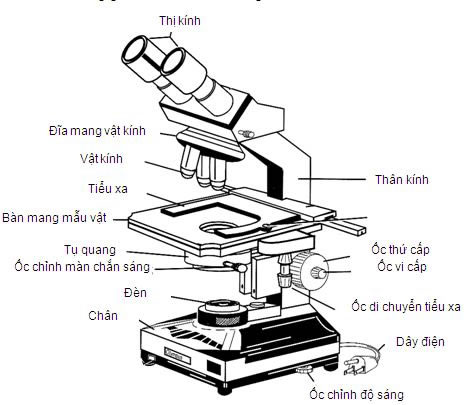
Kính hiển vi là một dụng cụ quang học có khả năng tạo ra hình ảnh phóng đại của các vật thể nhỏ, giúp chúng ta quan sát chi tiết hơn. Một trong những đặc tính quan trọng của kính hiển vi là "số bội giác", hay còn gọi là độ phóng đại của kính hiển vi.
1. Định Nghĩa Số Bội Giác
Số bội giác của kính hiển vi là một đại lượng cho biết mức độ phóng đại của hình ảnh mà kính hiển vi tạo ra so với kích thước thực của vật thể. Nó được xác định bởi công thức:
Trường hợp ngắm chừng ở cực cận:
\[
G_c=\left |\frac{d_1'd_2'}{d_1d_2} \right |
\]
Trường hợp ngắm chừng ở vô cực:
\[
G_\infty =\left |k_1 \right | \cdot G_2=\frac{\delta \cdot OC_c}{f_1 \cdot f_2}
\]
- \(G_\infty\): số bội giác khi ngắm chừng ở vô cực.
- \(k_1\): số phóng đại của vật kính \(L_1\).
- \(G_2\): số bội giác của thị kính \(L_2\).
- \(\delta\): độ dài quang học.
- \(f_1\): tiêu cự của vật kính \(L_1\).
- \(f_2\): tiêu cự của thị kính \(L_2\).
- \(OC_c\): khoảng nhìn rõ gần nhất của mắt.
2. Ví Dụ Tính Số Bội Giác
Ví dụ, một kính hiển vi có các tiêu cự của vật kính và thị kính lần lượt là \(f_1 = 1\) cm và \(f_2 = 4\) cm. Độ dài quang học của kính là 16 cm. Người quan sát có mắt không bị tật và có khoảng cực cận \(OC_c = 20\) cm. Khi ngắm chừng ở vô cực, số bội giác của kính hiển vi được tính như sau:
\[
G_\infty = \frac{\delta \cdot OC_c}{f_1 \cdot f_2} = \frac{16 \cdot 20}{1 \cdot 4} = 80
\]
3. Ứng Dụng Số Bội Giác
Số bội giác của kính hiển vi được ứng dụng trong nhiều lĩnh vực khác nhau, đặc biệt là trong sinh học và y học để quan sát các vi sinh vật, tế bào, và các cấu trúc nhỏ khác mà mắt thường không thể nhìn thấy. Nó cũng rất quan trọng trong nghiên cứu vật liệu và công nghệ nano.
4. Kết Luận
Số bội giác là một thông số kỹ thuật quan trọng của kính hiển vi, giúp xác định khả năng phóng đại của thiết bị. Việc hiểu và sử dụng đúng số bội giác giúp các nhà khoa học và kỹ thuật viên có thể quan sát và nghiên cứu các mẫu vật nhỏ với độ chi tiết cao nhất.
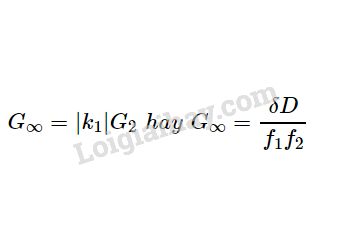
.png)
Mục Lục Tổng Hợp
Dưới đây là mục lục chi tiết cho bài viết về "Số Bội Giác Của Kính Hiển Vi", bao gồm các khái niệm, công thức, ứng dụng, và các ví dụ tính toán chi tiết:
- Giới thiệu về Kính Hiển Vi
- Khái quát về kính hiển vi và vai trò trong khoa học
- Cấu tạo cơ bản của kính hiển vi
- Khái Niệm Số Bội Giác
- Định nghĩa số bội giác
- Vai trò của số bội giác trong việc quan sát
- Công Thức Tính Số Bội Giác
- Công thức tổng quát
- Công thức trong trường hợp ngắm chừng ở cực cận
- Công thức trong trường hợp ngắm chừng ở vô cực
- Ví dụ minh họa
- Ứng Dụng Của Số Bội Giác
- Ứng dụng trong sinh học
- Ứng dụng trong y học
- Ứng dụng trong nghiên cứu vật liệu
- Các Loại Kính Hiển Vi Và Số Bội Giác
- Kính hiển vi quang học
- Kính hiển vi điện tử
- Kính hiển vi lực nguyên tử
- Các Bài Tập Và Ví Dụ Tính Toán Số Bội Giác
- Bài tập với kính hiển vi tiêu cự ngắn
- Bài tập với kính hiển vi tiêu cự dài
- So Sánh Số Bội Giác Giữa Các Loại Kính Hiển Vi
- Số bội giác tối đa
- Ưu và nhược điểm của từng loại
- Kết Luận
- Tầm quan trọng của số bội giác trong nghiên cứu khoa học
- Những yếu tố ảnh hưởng đến số bội giác
1. Giới Thiệu Về Kính Hiển Vi
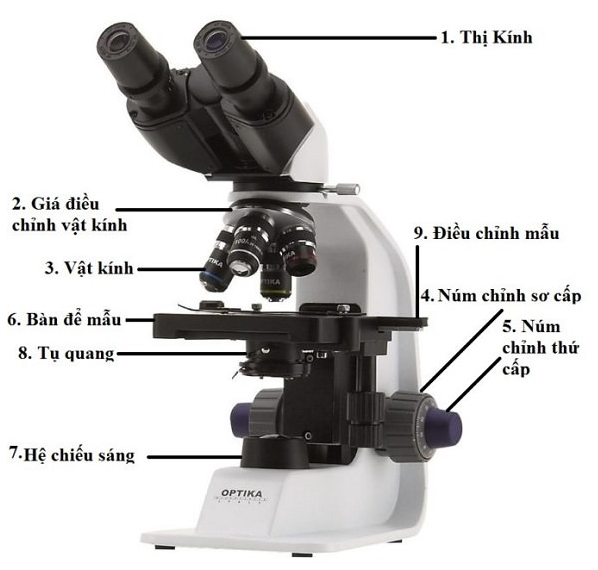
Kính hiển vi là một dụng cụ quang học được sử dụng để quan sát các vật thể cực nhỏ mà mắt thường không thể nhìn thấy rõ. Với cấu tạo gồm hai hệ thấu kính chính là vật kính và thị kính, kính hiển vi có khả năng tạo ra các hình ảnh phóng đại với độ bội giác rất cao. Vật kính là một thấu kính hội tụ có tiêu cự nhỏ, trong khi thị kính là một kính lúp giúp phóng đại hình ảnh của vật được tạo bởi vật kính. Độ phóng đại và sự chi tiết của hình ảnh phụ thuộc vào nhiều yếu tố như tiêu cự của các thấu kính và khoảng cách giữa chúng.

2. Khái Niệm Về Số Bội Giác
Số bội giác của kính hiển vi là một đại lượng quan trọng, cho biết mức độ phóng đại của hình ảnh mà kính hiển vi có thể tạo ra từ một vật thể nhỏ. Số bội giác được xác định dựa trên công thức:
Trong đó:
- \(f_1\): Tiêu cự của vật kính
- \(f_2\): Tiêu cự của thị kính
- \(d\): Khoảng cách từ mắt đến điểm cực cận (thường là 25 cm)
- \(\delta\): Độ dài quang học của kính hiển vi
Số bội giác càng lớn, hình ảnh quan sát được càng chi tiết. Đây là lý do tại sao kính hiển vi có số bội giác cao rất quan trọng trong các lĩnh vực như sinh học, y học và nghiên cứu vật liệu.
3. Công Thức Tính Số Bội Giác
Số bội giác của kính hiển vi là đại lượng mô tả khả năng phóng đại của hình ảnh qua hệ thống quang học của kính. Để tính số bội giác \(G\) của kính hiển vi, ta sử dụng công thức sau:
Trong đó:
- \(G_1 = \frac{d}{f_1}\): Số phóng đại của vật kính, với \(d\) là khoảng cách từ vật kính đến vật quan sát, \(f_1\) là tiêu cự của vật kính.
- \(G_2 = \frac{OC_c}{f_2}\): Số bội giác của thị kính, với \(OC_c\) là khoảng nhìn rõ gần nhất của mắt (thường là 25 cm), \(f_2\) là tiêu cự của thị kính.
Công thức này cho thấy số bội giác tổng thể của kính hiển vi phụ thuộc vào cả tiêu cự của vật kính và thị kính, cũng như khoảng cách từ mắt đến vật quan sát. Trong trường hợp ngắm chừng ở vô cực, số bội giác \(G_{\infty}\) được tính theo công thức:
Ở đây, \(\delta\) là độ dài quang học của kính hiển vi, và các yếu tố khác như trên.
Việc hiểu rõ công thức này rất quan trọng để điều chỉnh kính hiển vi đạt hiệu quả cao nhất trong các thí nghiệm và quan sát khoa học.

4. Ứng Dụng Của Số Bội Giác
Số bội giác của kính hiển vi có nhiều ứng dụng quan trọng trong các lĩnh vực khoa học và công nghệ. Dưới đây là một số ứng dụng tiêu biểu:
- Sinh học: Số bội giác cao giúp các nhà sinh học quan sát được các cấu trúc tế bào, vi khuẩn, virus và các sinh vật nhỏ khác, hỗ trợ trong việc nghiên cứu, chẩn đoán và phát triển thuốc.
- Y học: Trong y học, số bội giác của kính hiển vi giúp phát hiện các tế bào bất thường, nghiên cứu mô bệnh học, và hỗ trợ trong việc chẩn đoán bệnh tật một cách chính xác.
- Vật liệu học: Số bội giác cao cho phép các kỹ sư vật liệu kiểm tra các khuyết tật, cấu trúc tinh thể, và các đặc tính bề mặt của vật liệu ở cấp độ vi mô, giúp cải tiến chất lượng và độ bền của sản phẩm.
- Địa chất: Kính hiển vi với số bội giác lớn được sử dụng để phân tích cấu trúc đá, khoáng chất, và các mẫu vật địa chất, cung cấp thông tin quý giá về lịch sử và sự hình thành của Trái Đất.
- Ngành giáo dục: Trong giảng dạy và học tập, số bội giác giúp sinh viên và giảng viên quan sát chi tiết các mẫu vật, từ đó hiểu rõ hơn về cấu trúc và chức năng của chúng.
Sự ứng dụng đa dạng của số bội giác trong các lĩnh vực trên không chỉ giúp nâng cao chất lượng nghiên cứu và phát triển, mà còn đóng góp quan trọng vào việc bảo vệ sức khỏe và cải thiện chất lượng cuộc sống.
XEM THÊM:
5. Các Ví Dụ Tính Toán Số Bội Giác
Dưới đây là một số ví dụ cụ thể về cách tính số bội giác của kính hiển vi trong các trường hợp khác nhau:
5.1. Ví Dụ Với Kính Hiển Vi Tiêu Cự Ngắn
Giả sử bạn có một kính hiển vi với các thông số sau:
- Tiêu cự vật kính: \( f_1 = 1 \, cm \)
- Tiêu cự thị kính: \( f_2 = 4 \, cm \)
- Độ dài quang học của kính: \( l = 16 \, cm \)
- Khoảng cực cận của mắt người quan sát: \( OC_c = 20 \, cm \)
Người quan sát đặt mắt ở vô cực để ngắm chừng. Số bội giác của kính hiển vi khi ngắm chừng ở vô cực được tính theo công thức:
Trong đó:
- \( \delta = l - f_1 - f_2 \)
- Với \( l = 16 \, cm \), \( f_1 = 1 \, cm \), \( f_2 = 4 \, cm \), ta có \( \delta = 16 - 1 - 4 = 11 \, cm \)
- Vì \( OC_c = 20 \, cm \), số bội giác sẽ là:
Như vậy, số bội giác của kính hiển vi trong trường hợp này là 55 lần.
5.2. Ví Dụ Với Kính Hiển Vi Tiêu Cự Dài
Xét một kính hiển vi khác có các thông số:
- Tiêu cự vật kính: \( f_1 = 1 \, cm \)
- Tiêu cự thị kính: \( f_2 = 5 \, cm \)
- Độ dài quang học của kính: \( l = 15 \, cm \)
- Khoảng cực cận của mắt người quan sát: \( OC_c = 25 \, cm \)
Trong trường hợp này, ta tính độ dài quang học \( \delta \) và số bội giác khi ngắm chừng ở vô cực như sau:
Do đó, số bội giác của kính hiển vi trong trường hợp này là 45 lần.
Các ví dụ trên giúp minh họa rõ ràng cách tính số bội giác của kính hiển vi dựa trên các thông số kỹ thuật cơ bản. Việc nắm vững công thức và quy trình tính toán là rất quan trọng để có thể sử dụng kính hiển vi một cách hiệu quả.

6. So Sánh Số Bội Giác Giữa Các Loại Kính Hiển Vi
Số bội giác của kính hiển vi là một thông số quan trọng, giúp xác định khả năng phóng đại của kính. Số bội giác được xác định bởi sự kết hợp giữa vật kính và thị kính trong hệ thống kính. Mỗi loại kính hiển vi khác nhau sẽ có số bội giác khác nhau tùy thuộc vào cấu tạo và mục đích sử dụng.
- Kính Hiển Vi Quang Học:
Kính hiển vi quang học là loại kính phổ biến nhất, sử dụng ánh sáng khả kiến để phóng đại hình ảnh của vật thể. Số bội giác của loại kính này thường dao động từ 40x đến 2000x, phù hợp với các ứng dụng cơ bản như quan sát mẫu sinh học hoặc nghiên cứu tế bào. Kính hiển vi quang học có ưu điểm là dễ sử dụng và chi phí thấp, nhưng giới hạn bởi độ phân giải.
- Kính Hiển Vi Điện Tử:
Kính hiển vi điện tử sử dụng chùm điện tử thay vì ánh sáng để tạo ảnh, giúp đạt được độ phóng đại rất cao, từ 10,000x đến 1,000,000x. Kính này có thể quan sát chi tiết cấu trúc của mẫu ở cấp độ nguyên tử, được sử dụng nhiều trong nghiên cứu vật liệu và sinh học phân tử. Tuy nhiên, loại kính này đòi hỏi môi trường chân không và có chi phí vận hành cao.
- Kính Hiển Vi Quét Đầu Dò (Scanning Probe Microscope - SPM):
Loại kính này không sử dụng ánh sáng hay chùm điện tử mà dựa trên tương tác vật lý giữa đầu dò và bề mặt mẫu để tạo ảnh. Số bội giác của SPM có thể lên đến cấp độ nguyên tử, vượt trội so với kính hiển vi quang học và điện tử. Tuy nhiên, phương pháp này phức tạp và đòi hỏi kỹ thuật cao, chủ yếu được dùng trong nghiên cứu chuyên sâu.
Kết luận, mỗi loại kính hiển vi có ưu và nhược điểm riêng về số bội giác và khả năng ứng dụng. Kính hiển vi quang học là lựa chọn tốt cho các ứng dụng cơ bản, trong khi kính hiển vi điện tử và quét đầu dò phù hợp với các nghiên cứu chuyên sâu yêu cầu độ phân giải cao.

7. Lời Kết
Qua những phân tích và so sánh về số bội giác của các loại kính hiển vi, chúng ta có thể thấy rằng kính hiển vi là một công cụ không thể thiếu trong việc nghiên cứu khoa học, đặc biệt là trong các lĩnh vực sinh học, y học và công nghệ nano. Số bội giác của kính hiển vi đóng vai trò quan trọng trong việc quyết định độ rõ nét và chi tiết của hình ảnh quan sát, từ đó ảnh hưởng trực tiếp đến khả năng phân tích và khám phá các cấu trúc vi mô.
Việc lựa chọn kính hiển vi phù hợp với nhu cầu nghiên cứu không chỉ dựa vào số bội giác mà còn phụ thuộc vào nhiều yếu tố khác như tiêu cự, độ dài quang học và điều kiện ngắm chừng. Các công thức và ví dụ cụ thể đã giúp chúng ta hiểu rõ hơn về cách tính và ứng dụng số bội giác trong thực tiễn, đồng thời cung cấp những cơ sở lý thuyết vững chắc để áp dụng trong các thí nghiệm và nghiên cứu thực tế.
Hy vọng rằng qua bài viết này, bạn đã nắm vững được các khái niệm và công thức quan trọng liên quan đến số bội giác của kính hiển vi, cũng như hiểu rõ hơn về sự khác biệt giữa các loại kính hiển vi. Điều này sẽ giúp bạn có những lựa chọn sáng suốt và hiệu quả hơn trong công việc nghiên cứu và ứng dụng khoa học.