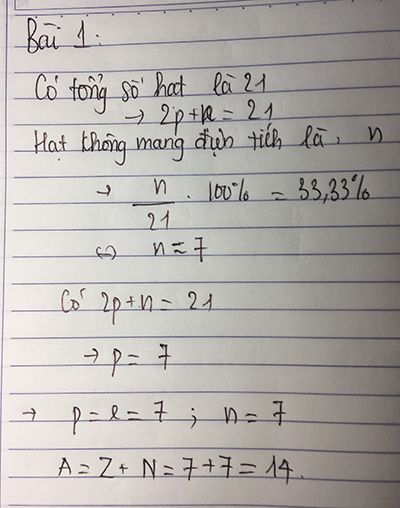Quang Phổ Vạch Của Nguyên Tử Hidro: Khám Phá Bí Ẩn Ánh Sáng Và Cấu Trúc Nguyên Tử

Quang phổ vạch của nguyên tử hidro là một chủ đề quan trọng trong lĩnh vực vật lý nguyên tử. Đây là hiện tượng xuất hiện khi các electron trong nguyên tử hidro chuyển từ mức năng lượng cao xuống mức năng lượng thấp, phát ra các photon có bước sóng đặc trưng, tạo thành các vạch quang phổ riêng biệt.

Cấu Trúc Quang Phổ Vạch Của Nguyên Tử Hidro

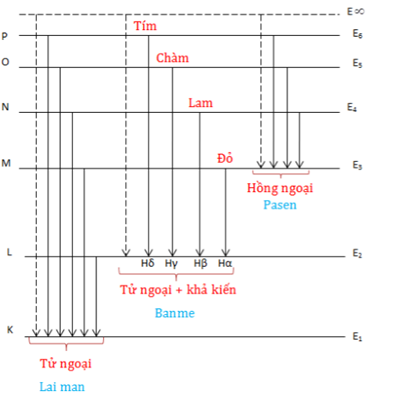
Cấu trúc quang phổ vạch của nguyên tử hidro có thể được hiểu qua các dãy khác nhau, mỗi dãy tương ứng với sự chuyển dời của electron giữa các mức năng lượng xác định:

• Dãy Lyman: Các chuyển dời về mức \( n = 1 \), phát xạ trong vùng tử ngoại.
• Dãy Balmer: Các chuyển dời về mức \( n = 2 \), phát xạ trong vùng ánh sáng nhìn thấy.
• Dãy Paschen: Các chuyển dời về mức \( n = 3 \), phát xạ trong vùng hồng ngoại gần.
• Dãy Brackett: Các chuyển dời về mức \( n = 4 \), phát xạ trong vùng hồng ngoại trung.
• Dãy Pfund: Các chuyển dời về mức \( n = 5 \), phát xạ trong vùng hồng ngoại xa.

Công Thức Liên Quan Đến Quang Phổ Vạch

Các mức năng lượng của electron trong nguyên tử hidro được xác định bằng công thức:

\[ E_n = - \frac{13.6 \, \text{eV}}{n^2} \]

trong đó \( E_n \) là năng lượng của mức \( n \), và \( n \) là số lượng tử chính.

Khi electron chuyển từ mức năng lượng cao xuống mức thấp hơn, năng lượng của photon phát ra được tính bằng:

\[ E = E_{n_2} - E_{n_1} \]

Bước sóng của photon phát ra được xác định bằng phương trình Rydberg:

\[ \frac{1}{\lambda} = R_H \left( \frac{1}{n_1^2} - \frac{1}{n_2^2} \right) \]

trong đó:

• \( \lambda \) là bước sóng của photon.
• \( R_H \) là hằng số Rydberg, khoảng \( 1.097 \times 10^7 \, \text{m}^{-1} \).
• \( n_1 \) và \( n_2 \) là các số nguyên, với \( n_2 > n_1 \).

Ứng Dụng Của Quang Phổ Vạch Của Nguyên Tử Hidro

Quang phổ vạch của nguyên tử hidro không chỉ có ý nghĩa trong nghiên cứu cơ bản mà còn có nhiều ứng dụng thực tiễn trong các lĩnh vực như:

• Thiên văn học: Dùng để xác định thành phần hóa học của các ngôi sao và các thiên thể khác.
• Vật lý nguyên tử: Giúp hiểu rõ hơn về cấu trúc nguyên tử và các mức năng lượng của electron.
• Hóa học phân tích: Sử dụng trong phân tích các nguyên tố hóa học thông qua quang phổ phát xạ.

Kết Luận

Quang phổ vạch của nguyên tử hidro là một trong những hiện tượng quan trọng giúp chúng ta hiểu rõ hơn về thế giới vi mô của nguyên tử. Từ đó, nó mở ra nhiều ứng dụng thực tiễn trong nghiên cứu và công nghệ, góp phần vào sự phát triển của khoa học và đời sống.

Quang phổ vạch của nguyên tử hidro là một hiện tượng quan trọng trong vật lý nguyên tử, được phát hiện lần đầu tiên bởi nhà vật lý Joseph von Fraunhofer. Đây là một phần của quang phổ điện từ, trong đó các vạch sáng hoặc tối xuất hiện khi ánh sáng từ một nguồn nhất định được phân tích bằng lăng kính hoặc mạng nhiễu xạ.

Các vạch quang phổ xuất hiện do sự chuyển đổi năng lượng của các electron trong nguyên tử. Khi một electron nhảy từ một mức năng lượng cao xuống một mức năng lượng thấp hơn, nó phát ra một photon với năng lượng tương ứng, tạo ra một vạch sáng trong quang phổ. Ngược lại, nếu electron hấp thụ một photon và nhảy lên mức năng lượng cao hơn, sẽ tạo ra một vạch tối trong quang phổ hấp thụ.

• Cấu trúc vạch: Mỗi vạch quang phổ đại diện cho một bước nhảy cụ thể của electron giữa các mức năng lượng khác nhau trong nguyên tử.
• Dãy vạch: Các dãy vạch khác nhau (như dãy Lyman, Balmer, Paschen) tương ứng với các bước nhảy khác nhau của electron, từ mức năng lượng cao hơn về mức năng lượng cơ bản.
• Ứng dụng: Quang phổ vạch được sử dụng rộng rãi trong việc phân tích thành phần hóa học của các nguyên tố, xác định các đặc tính vật lý của sao và thiên hà, và trong nhiều lĩnh vực nghiên cứu khác.

Để hiểu rõ hơn, công thức tính năng lượng của một photon phát ra trong quá trình chuyển đổi năng lượng của electron trong nguyên tử hidro là:

\[
E = h \cdot \nu = h \cdot \frac{c}{\lambda}
\]

Trong đó:

• \(E\): Năng lượng của photon (Joule)
• \(h\): Hằng số Planck (\(6.626 \times 10^{-34}\) Js)
• \(\nu\): Tần số của ánh sáng (Hz)
• \(c\): Vận tốc ánh sáng (\(3 \times 10^{8}\) m/s)
• \(\lambda\): Bước sóng của ánh sáng (m)

Như vậy, quang phổ vạch của nguyên tử hidro không chỉ là công cụ quan trọng trong việc nghiên cứu vật lý nguyên tử mà còn có ứng dụng rộng rãi trong các lĩnh vực khoa học khác.

Trong nghiên cứu về quang phổ vạch của nguyên tử hidro, có một số công thức quan trọng giúp mô tả quá trình phát xạ và hấp thụ ánh sáng. Dưới đây là những công thức chính liên quan đến quang phổ vạch:

1. Công Thức Rydberg:

Công thức Rydberg được sử dụng để tính toán bước sóng \(\lambda\) của các vạch quang phổ:

\[
\frac{1}{\lambda} = R \left( \frac{1}{n_1^2} - \frac{1}{n_2^2} \right)
\]

• \(\lambda\): Bước sóng của ánh sáng phát ra (m)
• \(R\): Hằng số Rydberg cho hidro (\(1.097 \times 10^7\) m\(^{-1}\))
• \(n_1\), \(n_2\): Các số nguyên đại diện cho các mức năng lượng (với \(n_2 > n_1\))

2. Công Thức Liên Quan Đến Tần Số Ánh Sáng:

Khi electron chuyển từ mức năng lượng cao xuống mức năng lượng thấp hơn, tần số ánh sáng phát ra được tính bằng:

\[
\nu = \frac{E_2 - E_1}{h}
\]

• \(\nu\): Tần số ánh sáng phát ra (Hz)
• \(E_2\), \(E_1\): Năng lượng của các mức (J)
• \(h\): Hằng số Planck (\(6.626 \times 10^{-34}\) Js)

3. Công Thức Liên Hệ Giữa Năng Lượng Và Bước Sóng:

Năng lượng của photon phát ra cũng có thể được liên hệ với bước sóng bằng công thức:

\[
E = \frac{h \cdot c}{\lambda}
\]

• \(E\): Năng lượng của photon (J)
• \(h\): Hằng số Planck (\(6.626 \times 10^{-34}\) Js)
• \(c\): Vận tốc ánh sáng (\(3 \times 10^8\) m/s)
• \(\lambda\): Bước sóng của ánh sáng (m)

4. Công Thức Liên Hệ Giữa Năng Lượng Và Tần Số:

Năng lượng của photon cũng có thể được tính từ tần số của ánh sáng phát ra:

\[
E = h \cdot \nu
\]

• \(E\): Năng lượng của photon (J)
• \(h\): Hằng số Planck (\(6.626 \times 10^{-34}\) Js)
• \(\nu\): Tần số ánh sáng phát ra (Hz)

Những công thức trên giúp chúng ta hiểu rõ hơn về cách các vạch quang phổ của nguyên tử hidro được hình thành và tính toán các đặc tính của ánh sáng phát ra.

Quang phổ vạch của nguyên tử hidro không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tiễn quan trọng. Dưới đây là một số ứng dụng chính:

1. Phân Tích Thành Phần Nguyên Tố:

Quang phổ vạch được sử dụng để xác định thành phần nguyên tố trong các mẫu vật liệu. Các nhà khoa học có thể phân tích ánh sáng phát ra từ một chất để xác định các nguyên tố có mặt dựa trên các vạch quang phổ đặc trưng.

2. Nghiên Cứu Vật Lý Thiên Văn:

Trong thiên văn học, quang phổ vạch giúp xác định thành phần hóa học của các ngôi sao và thiên thể khác trong vũ trụ. Bằng cách quan sát các vạch quang phổ, các nhà thiên văn học có thể xác định các nguyên tố tồn tại trong các ngôi sao, đo lường tốc độ di chuyển và thậm chí xác định khoảng cách đến các thiên thể xa xôi.

3. Ứng Dụng Trong Y Khoa:

Quang phổ vạch cũng được ứng dụng trong y khoa, đặc biệt trong việc chẩn đoán bệnh. Phổ hồng ngoại và quang phổ hấp thụ được sử dụng để phân tích thành phần hóa học trong cơ thể, giúp phát hiện các bệnh lý và theo dõi sức khỏe của bệnh nhân.

4. Kiểm Soát Chất Lượng Trong Công Nghiệp:

Trong công nghiệp, quang phổ vạch được sử dụng để kiểm tra chất lượng của các sản phẩm, đặc biệt là trong ngành luyện kim và sản xuất vật liệu. Các vạch quang phổ có thể giúp phát hiện tạp chất và xác định tính chất của vật liệu một cách chính xác.

5. Giáo Dục Và Nghiên Cứu Khoa Học:

Quang phổ vạch là một công cụ quan trọng trong giáo dục và nghiên cứu khoa học, giúp sinh viên và các nhà khoa học hiểu rõ hơn về cấu trúc nguyên tử và các hiện tượng liên quan đến ánh sáng.

Nhờ những ứng dụng đa dạng này, quang phổ vạch đã trở thành một công cụ không thể thiếu trong nhiều lĩnh vực khoa học và công nghệ hiện đại.

Dưới đây là một số bài toán và ví dụ điển hình liên quan đến quang phổ vạch của nguyên tử hidro, giúp học sinh nắm vững kiến thức và cách áp dụng công thức vào thực tiễn.

Bài toán 1: Tính bước sóng của bức xạ phát ra

• Đề bài: Cho một nguyên tử hidro chuyển từ mức năng lượng \(n_2 = 3\) về mức năng lượng \(n_1 = 2\). Tính bước sóng của bức xạ phát ra.
• Lời giải: Sử dụng công thức Rydberg: \[ \frac{1}{\lambda} = R \left(\frac{1}{n_1^2} - \frac{1}{n_2^2}\right) \] Trong đó \(R\) là hằng số Rydberg, \(n_1\) và \(n_2\) là các mức năng lượng. Thay các giá trị vào, ta tính được bước sóng \(\lambda\).

Bài toán 2: Xác định số vạch quang phổ

• Đề bài: Khi một electron trong nguyên tử hidro chuyển từ mức năng lượng \(n=4\) về mức năng lượng cơ bản \(n=1\), xác định số vạch quang phổ có thể quan sát được.
• Lời giải: Số vạch quang phổ được xác định bằng số lượng các chuyển mức năng lượng có thể có giữa các mức này. Công thức tổng quát để tính số vạch là: \[ S = \frac{n(n-1)}{2} \] Với \(n=4\), số vạch quang phổ sẽ là \(S=6\).

Ví dụ 1: Minh họa chuỗi quang phổ Balmer

• Trong chuỗi Balmer, các vạch quang phổ được phát ra khi electron chuyển từ các mức năng lượng cao hơn về mức \(n=2\). Đây là các vạch trong vùng nhìn thấy của quang phổ và được ứng dụng rộng rãi trong việc nghiên cứu cấu trúc nguyên tử.

Ví dụ 2: Phân tích quang phổ thiên văn

• Các nhà thiên văn học thường sử dụng các vạch quang phổ hidro để phân tích thành phần hóa học của các ngôi sao và thiên thể khác. Ví dụ, bằng cách quan sát các vạch quang phổ trong chuỗi Lyman và Balmer, có thể xác định được các đặc tính của ngôi sao như nhiệt độ và vận tốc chuyển động.