Chủ đề lý thuyết điện từ trường: Lý thuyết điện từ trường là một phần quan trọng của vật lý, giúp chúng ta hiểu rõ hơn về mối quan hệ giữa điện và từ trường. Bài viết này cung cấp kiến thức sâu rộng về các khái niệm cơ bản, phương trình Maxwell và ứng dụng thực tiễn, giúp học sinh và sinh viên nắm vững lý thuyết và áp dụng vào các bài tập thực hành.
Mục lục
Lý Thuyết Điện Từ Trường
Lý thuyết điện từ trường là một phần quan trọng trong vật lý học, đặc biệt trong chương trình Vật lý lớp 12. Nó bao gồm các khái niệm về điện trường, từ trường và mối quan hệ giữa chúng. Dưới đây là nội dung chi tiết về lý thuyết điện từ trường:
I. Mối quan hệ giữa điện trường và từ trường
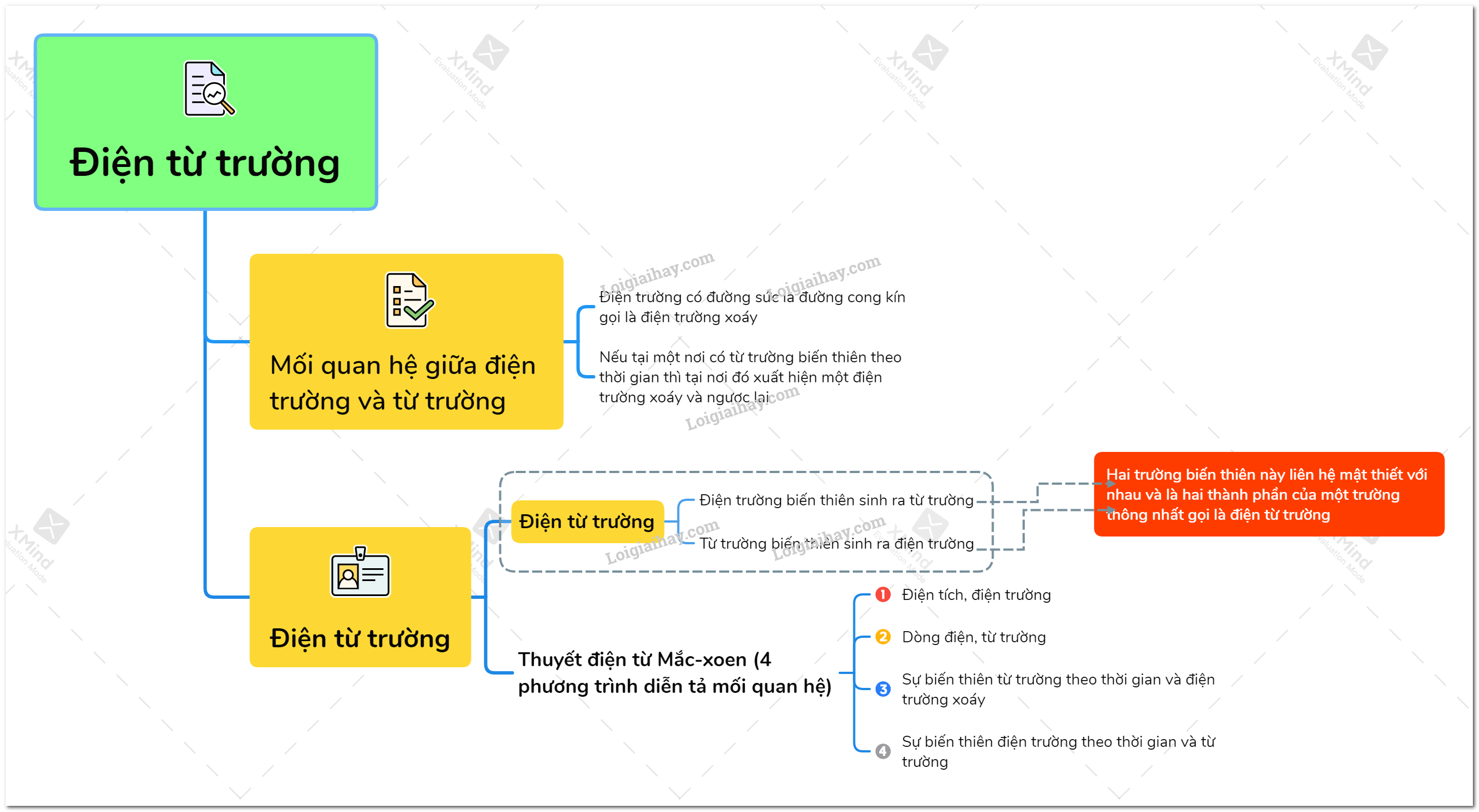
Điện trường và từ trường không tồn tại độc lập mà có mối liên hệ mật thiết với nhau. Khi một trong hai trường biến thiên theo thời gian, nó sẽ tạo ra trường còn lại:
- Nếu từ trường biến thiên theo thời gian, tại nơi đó xuất hiện điện trường xoáy.
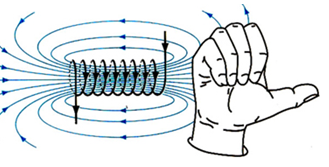
- Nếu điện trường biến thiên theo thời gian, tại nơi đó xuất hiện từ trường với đường sức khép kín.
II. Điện từ trường
Điện trường và từ trường cùng tồn tại và biến đổi trong một không gian gọi là điện từ trường. Một điện từ trường được đặc trưng bởi các đại lượng vật lý như:
- Cường độ điện trường \(E\)
- Độ điện dịch \(D\)
- Cảm ứng từ \(B\)
- Cường độ từ trường \(H\)
III. Phương trình Maxwell
Phương trình Maxwell là nền tảng của lý thuyết điện từ trường, bao gồm bốn phương trình chính:
- Định luật Gauss về điện: Mô tả cách điện tích tạo ra điện trường.
- Định luật Gauss về từ: Tuyên bố rằng không có vật chất nào gọi là từ tích.
- Định luật Faraday: Mô tả cách từ trường biến thiên theo thời gian tạo ra điện trường.
- Định luật Ampère-Maxwell: Mô tả cách dòng điện và điện trường biến thiên theo thời gian tạo ra từ trường.
IV. Ứng dụng của lý thuyết điện từ trường
Lý thuyết điện từ trường có nhiều ứng dụng trong thực tiễn, bao gồm:
- Thiết kế và vận hành máy phát điện, động cơ điện.
- Ứng dụng trong viễn thông và truyền thông qua sóng điện từ.
- Thiết kế các thiết bị đo lường và cảm biến điện từ.
Những kiến thức này không chỉ là cơ sở để hiểu rõ hơn về thế giới vật lý mà còn ứng dụng rộng rãi trong các lĩnh vực kỹ thuật và công nghệ.
.png)
1. Giới thiệu về điện từ trường
Điện từ trường là một khái niệm quan trọng trong vật lý học, miêu tả mối quan hệ giữa điện trường và từ trường. Hai trường này luôn gắn kết với nhau và thay đổi cùng nhau. Hiện tượng này được miêu tả thông qua các phương trình Maxwell, giúp chúng ta hiểu rõ hơn về cách mà điện từ trường hoạt động trong các vật chất và không gian.
Điện trường là vùng không gian xung quanh một điện tích, trong đó lực điện tác dụng lên các điện tích khác. Từ trường, mặt khác, là vùng không gian xung quanh nam châm hoặc dòng điện, nơi lực từ tác dụng lên các hạt mang điện hoặc các vật có từ tính.
- Điện trường: Được sinh ra xung quanh các hạt mang điện và được miêu tả bởi các vectơ điện trường. Điện trường có thể được tính bằng công thức \(\mathbf{E} = \frac{\mathbf{F}}{q}\), trong đó \(\mathbf{E}\) là cường độ điện trường, \(\mathbf{F}\) là lực tác dụng lên điện tích thử, và \(q\) là giá trị của điện tích.
- Từ trường: Được tạo ra xung quanh các dòng điện hoặc các vật có từ tính và được miêu tả bởi vectơ từ trường \(\mathbf{B}\). Từ trường có thể được tính toán bằng định luật Biot-Savart và định lý Ampère, với công thức cơ bản là \(\mathbf{B} = \mu_0 \frac{I}{2 \pi r}\), trong đó \(\mu_0\) là độ từ thẩm của chân không, \(I\) là cường độ dòng điện, và \(r\) là khoảng cách từ dòng điện.
Quan hệ giữa điện trường và từ trường được hiểu rõ thông qua thuyết điện từ Maxwell, trong đó bốn phương trình cơ bản mô tả cách mà các trường này tương tác và ảnh hưởng lẫn nhau. Các phương trình Maxwell cho thấy rằng sự thay đổi của từ trường sẽ sinh ra điện trường và ngược lại, sự thay đổi của điện trường sẽ tạo ra từ trường.
| Phương trình Maxwell | Mô tả |
|---|---|
| Phương trình Gauss cho điện trường | \[\nabla \cdot \mathbf{E} = \frac{\rho}{\varepsilon_0}\] |
| Phương trình Gauss cho từ trường | \[\nabla \cdot \mathbf{B} = 0\] |
| Phương trình Faraday về cảm ứng điện từ | \[\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}\] |
| Phương trình Ampère-Maxwell | \[\nabla \times \mathbf{B} = \mu_0 \mathbf{J} + \mu_0 \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t}\] |
Hiểu rõ về điện từ trường và các phương trình Maxwell là cơ sở quan trọng để nắm vững các hiện tượng vật lý khác như sóng điện từ, bức xạ, và truyền dẫn năng lượng trong không gian. Những khái niệm này không chỉ quan trọng trong nghiên cứu khoa học mà còn có ứng dụng rộng rãi trong công nghệ hiện đại như truyền thông, điện tử, và y tế.
2. Thuyết điện từ Maxwell
Thuyết điện từ Maxwell là một trong những nền tảng quan trọng của vật lý hiện đại, đưa ra các phương trình mô tả sự tương tác giữa điện trường và từ trường. Được phát triển bởi James Clerk Maxwell vào thế kỷ 19, thuyết này đã tổng hợp các định luật trước đó về điện và từ thành một hệ thống lý thuyết hoàn chỉnh, giải thích các hiện tượng điện từ một cách toàn diện.
Các phương trình Maxwell gồm bốn phương trình chính, mỗi phương trình mô tả một khía cạnh khác nhau của điện từ trường:
- Phương trình Gauss cho điện trường: Phương trình này miêu tả mối quan hệ giữa điện trường \(\mathbf{E}\) và điện tích \(\rho\). Nó cho thấy rằng điện tích tạo ra một điện trường trong không gian xung quanh nó. Công thức của phương trình này là: \[ \nabla \cdot \mathbf{E} = \frac{\rho}{\varepsilon_0} \] trong đó \(\nabla \cdot \mathbf{E}\) là sự phân kỳ của điện trường, \(\rho\) là mật độ điện tích và \(\varepsilon_0\) là hằng số điện môi của chân không.
- Phương trình Gauss cho từ trường: Phương trình này khẳng định rằng không có đơn cực từ tồn tại, tức là từ trường \(\mathbf{B}\) luôn có đường sức khép kín. Công thức của phương trình này là: \[ \nabla \cdot \mathbf{B} = 0 \] trong đó \(\nabla \cdot \mathbf{B}\) là sự phân kỳ của từ trường.
- Phương trình Faraday về cảm ứng điện từ: Phương trình này diễn tả mối quan hệ giữa sự thay đổi của từ trường và sự xuất hiện của một điện trường. Khi từ trường biến thiên theo thời gian, nó sẽ sinh ra một điện trường xoáy. Công thức của phương trình này là: \[ \nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t} \] trong đó \(\nabla \times \mathbf{E}\) là sự xoáy của điện trường và \(\frac{\partial \mathbf{B}}{\partial t}\) là sự thay đổi của từ trường theo thời gian.
- Phương trình Ampère-Maxwell: Đây là sự mở rộng của định luật Ampère, bao gồm cả trường hợp khi điện trường biến đổi theo thời gian. Nó cho biết rằng dòng điện và sự thay đổi của điện trường đều tạo ra từ trường. Công thức của phương trình này là: \[ \nabla \times \mathbf{B} = \mu_0 \mathbf{J} + \mu_0 \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t} \] trong đó \(\nabla \times \mathbf{B}\) là sự xoáy của từ trường, \(\mathbf{J}\) là mật độ dòng điện, \(\mu_0\) là độ từ thẩm của chân không, và \(\frac{\partial \mathbf{E}}{\partial t}\) là sự thay đổi của điện trường theo thời gian.
Thuyết điện từ Maxwell không chỉ thống nhất các hiện tượng điện và từ thành một lý thuyết duy nhất, mà còn dự đoán sự tồn tại của sóng điện từ, mở đường cho sự phát triển của nhiều lĩnh vực khoa học và công nghệ như truyền thông vô tuyến, radar, và công nghệ không dây hiện đại.
Nhờ các phương trình Maxwell, chúng ta có thể hiểu sâu hơn về cách thức hoạt động của các thiết bị điện tử, cũng như các hiện tượng tự nhiên như ánh sáng, bức xạ điện từ và tác động của từ trường Trái Đất.

3. Trường điện từ và sóng điện từ
Trường điện từ là một trường vật lý được tạo ra bởi các hạt mang điện và các dòng điện. Nó bao gồm hai thành phần chính: điện trường \(\mathbf{E}\) và từ trường \(\mathbf{B}\). Hai trường này luôn liên kết và tương tác với nhau trong không gian và thời gian, tạo nên một trường điện từ động. Sóng điện từ là sự lan truyền của trường điện từ biến thiên theo thời gian trong không gian, và chúng bao gồm nhiều loại sóng như sóng radio, vi sóng, tia hồng ngoại, ánh sáng khả kiến, tia cực tím, tia X và tia gamma.
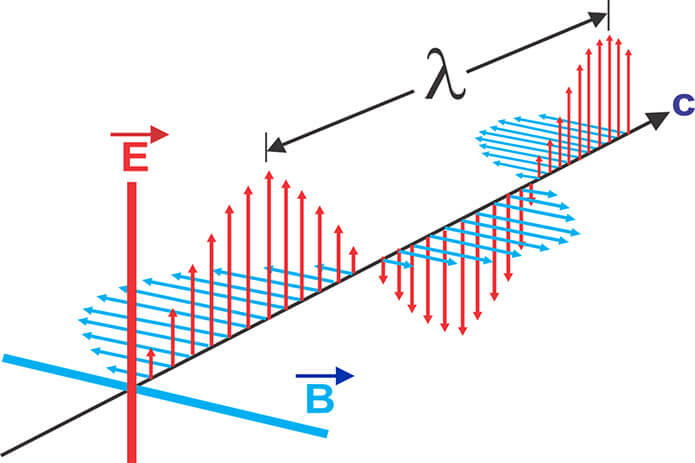
Sóng điện từ được sinh ra từ sự dao động của điện trường và từ trường vuông góc với nhau và cũng vuông góc với hướng truyền sóng. Điều này có nghĩa là khi một điện trường biến thiên sẽ tạo ra một từ trường biến thiên và ngược lại. Quá trình này tiếp tục lặp lại tạo ra sóng điện từ lan truyền trong không gian. Công thức mô tả mối quan hệ này là:
Trong đó:
- \(E_0\) và \(B_0\) là biên độ của điện trường và từ trường.
- \(k\) là số sóng, liên quan đến bước sóng \(\lambda\) theo công thức \(k = \frac{2\pi}{\lambda}\).
- \(\omega\) là tần số góc, liên quan đến tần số \(f\) của sóng qua công thức \(\omega = 2\pi f\).
- \(x\) là vị trí trong không gian và \(t\) là thời gian.
- \(\phi\) là pha ban đầu của sóng.
Trường điện từ và sóng điện từ đóng vai trò quan trọng trong nhiều lĩnh vực của khoa học và công nghệ. Chúng là cơ sở của nhiều ứng dụng quan trọng như truyền thông không dây, radar, y học (chụp X-quang, cộng hưởng từ MRI), và các công nghệ năng lượng mặt trời.
Sóng điện từ có thể được phân loại theo tần số và bước sóng của chúng, từ sóng dài có tần số thấp như sóng radio đến sóng ngắn có tần số cao như tia gamma. Bảng dưới đây mô tả các loại sóng điện từ chính và ứng dụng của chúng:
| Loại sóng | Tần số | Ứng dụng |
|---|---|---|
| Sóng radio | 3 Hz - 300 GHz | Phát thanh, truyền hình, liên lạc không dây |
| Vi sóng | 300 MHz - 300 GHz | Viễn thông, radar, lò vi sóng |
| Tia hồng ngoại | 300 GHz - 430 THz | Thiết bị điều khiển từ xa, chụp ảnh nhiệt |
| Ánh sáng khả kiến | 430 THz - 770 THz | Nhìn thấy được bởi mắt người, chiếu sáng |
| Tia cực tím | 770 THz - 30 PHz | Khử trùng, nghiên cứu sinh học |
| Tia X | 30 PHz - 30 EHz | Chụp X-quang y tế, kiểm tra an ninh |
| Tia gamma | > 30 EHz | Điều trị ung thư, nghiên cứu vật lý hạt nhân |
Việc hiểu biết về trường điện từ và sóng điện từ giúp chúng ta khai thác các đặc tính của chúng để phát triển các công nghệ tiên tiến và cải thiện chất lượng cuộc sống hàng ngày.

XEM THÊM:
4. Các phương trình và định luật liên quan
Trong phần này, chúng ta sẽ đi sâu vào các phương trình và định luật quan trọng trong lý thuyết điện từ trường, giúp bạn hiểu rõ hơn về cách thức hoạt động của trường điện từ trong các môi trường khác nhau.
4.1. Phương trình Poisson và Laplace
Phương trình Poisson và phương trình Laplace là hai phương trình quan trọng trong việc mô tả điện trường trong các môi trường khác nhau:
- Phương trình Poisson có dạng: \(\nabla^2 \phi = -\frac{\rho}{\epsilon}\), trong đó \(\phi\) là thế điện, \(\rho\) là mật độ điện tích, và \(\epsilon\) là hằng số điện môi của môi trường.
- Khi môi trường không có điện tích tự do (\(\rho = 0\)), phương trình Poisson trở thành phương trình Laplace: \(\nabla^2 \phi = 0\).
Các phương trình này được sử dụng để xác định thế điện tại các điểm khác nhau trong một trường điện từ, đặc biệt hữu ích trong các bài toán liên quan đến điện thế tĩnh.
4.2. Định lý Poynting về năng lượng trường điện từ
Định lý Poynting mô tả sự bảo toàn năng lượng trong trường điện từ và được thể hiện thông qua véctơ Poynting \(\mathbf{S}\):
Trong đó, \(\mathbf{E}\) là cường độ điện trường và \(\mathbf{H}\) là cường độ từ trường. Véctơ Poynting chỉ ra hướng và độ lớn của dòng năng lượng trong trường điện từ. Tổng năng lượng truyền qua một diện tích đơn vị trong một đơn vị thời gian được biểu diễn bởi tích phân véctơ Poynting qua diện tích đó:
4.3. Điều kiện bờ đối với các vectơ của trường điện từ
Điều kiện bờ là các điều kiện ràng buộc áp dụng cho các vectơ cường độ điện trường (\(\mathbf{E}\)) và cường độ từ trường (\(\mathbf{H}\)) tại biên giới giữa hai môi trường khác nhau. Các điều kiện này được sử dụng để giải quyết các bài toán biên liên quan đến sóng điện từ:
- Thành phần tiếp tuyến của \(\mathbf{E}\) và \(\mathbf{H}\) phải liên tục qua biên giới: \[ \mathbf{E}_{1t} = \mathbf{E}_{2t}, \quad \mathbf{H}_{1t} = \mathbf{H}_{2t} \]
- Thành phần pháp tuyến của \(\mathbf{D}\) và \(\mathbf{B}\) phải liên tục khi không có sự hiện diện của dòng điện bề mặt và mật độ điện tích bề mặt: \[ \mathbf{D}_{1n} = \mathbf{D}_{2n}, \quad \mathbf{B}_{1n} = \mathbf{B}_{2n} \]
Các điều kiện bờ này rất quan trọng trong việc tính toán và mô phỏng sóng điện từ, đặc biệt là trong các hệ thống anten, cáp dẫn sóng, và các thiết bị truyền sóng khác.

5. Ứng dụng và bài tập thực hành
5.1. Bài tập ứng dụng thực tế
Lý thuyết điện từ trường có nhiều ứng dụng quan trọng trong thực tế, từ các thiết bị gia dụng đến các hệ thống công nghệ cao. Để hiểu rõ hơn về các nguyên lý, dưới đây là một số bài tập ứng dụng cụ thể:
-
Bài tập 1: Tính toán cường độ từ trường trong một cuộn dây dẫn.
Cho một cuộn dây dẫn có \(N\) vòng, dòng điện \(I\) chạy qua, và chiều dài \(l\) của cuộn dây. Sử dụng định luật Ampère để tính toán cường độ từ trường \(B\) trong cuộn dây:
\[ B = \frac{\mu_0 N I}{l} \]Trong đó, \(\mu_0\) là hằng số từ trường của chân không.
-
Bài tập 2: Phân tích sóng điện từ trong không gian.
Một sóng điện từ lan truyền trong không gian với phương trình sóng điện trường \( \mathbf{E}(x,t) = E_0 \cos(kx - \omega t + \phi) \). Hãy xác định tần số \(f\), bước sóng \( \lambda \), và tốc độ truyền sóng \(c\).
\[ \lambda = \frac{c}{f}, \quad k = \frac{2\pi}{\lambda}, \quad \omega = 2\pi f \]
5.2. Phân tích và giải các bài toán về trường điện từ
Để giải quyết các bài toán về trường điện từ, cần nắm vững các phương trình Maxwell và các định luật cơ bản như định luật Coulomb, định luật Faraday, và định luật Biot-Savart. Dưới đây là một số ví dụ:
-
Bài toán 1: Tính lực tương tác giữa hai điện tích điểm.
Hai điện tích \( q_1 \) và \( q_2 \) cách nhau một khoảng \( r \). Áp dụng định luật Coulomb để tính lực tương tác \( F \) giữa chúng:
\[ F = k_e \frac{|q_1 q_2|}{r^2} \]Trong đó, \( k_e \) là hằng số Coulomb.
-
Bài toán 2: Xác định từ trường do dòng điện tạo ra tại một điểm trong không gian.
Sử dụng định luật Biot-Savart để tính toán từ trường \( d\mathbf{B} \) tại điểm cách một phần tử dòng điện \( d\mathbf{l} \) một khoảng \( r \):
\[ d\mathbf{B} = \frac{\mu_0 I \, d\mathbf{l} \times \hat{r}}{4 \pi r^2} \]
5.3. Các dạng bài tập trắc nghiệm và tự luận phổ biến
Các bài tập về điện từ trường thường xuất hiện dưới dạng trắc nghiệm hoặc tự luận trong các kỳ thi. Dưới đây là một số dạng bài tập phổ biến:
- Bài tập trắc nghiệm: Xác định hướng của từ trường, điện trường trong các cấu hình đơn giản.
- Bài tập tự luận: Phân tích chi tiết các hệ thống trường điện từ phức tạp, giải thích các hiện tượng như cảm ứng điện từ, bức xạ sóng điện từ.
6. Kết luận
Trường điện từ là một trong những khía cạnh quan trọng và cơ bản của vật lý học hiện đại. Lý thuyết điện từ trường không chỉ giúp giải thích các hiện tượng tự nhiên liên quan đến điện và từ, mà còn mở ra cánh cửa cho nhiều ứng dụng công nghệ tiên tiến trong đời sống hiện đại.
Thông qua các phương trình Maxwell, chúng ta đã hiểu rõ hơn về sự liên kết giữa điện trường và từ trường, đồng thời nhận ra rằng ánh sáng thực chất là một dạng sóng điện từ. Các kết quả lý thuyết này không chỉ có ý nghĩa trong việc phát triển khoa học cơ bản, mà còn là nền tảng cho các ứng dụng công nghệ như viễn thông, y tế, và năng lượng.
Có thể nói rằng, lý thuyết điện từ trường đã và đang đóng góp to lớn vào sự tiến bộ của khoa học và kỹ thuật, từ việc truyền tải thông tin không dây đến việc phát triển các thiết bị chẩn đoán hình ảnh trong y học. Việc nắm vững các kiến thức này sẽ giúp chúng ta hiểu rõ hơn về thế giới xung quanh và tạo ra những cải tiến vượt bậc trong tương lai.
Nhìn về phía trước, nghiên cứu về điện từ trường tiếp tục là một lĩnh vực đầy hứa hẹn, với nhiều tiềm năng để khám phá và ứng dụng. Những tiến bộ trong lĩnh vực này không chỉ giúp cải thiện cuộc sống hàng ngày mà còn mở ra những khả năng mới cho việc giải quyết các thách thức toàn cầu, từ việc phát triển nguồn năng lượng sạch đến việc cải thiện khả năng giao tiếp và kết nối toàn cầu.