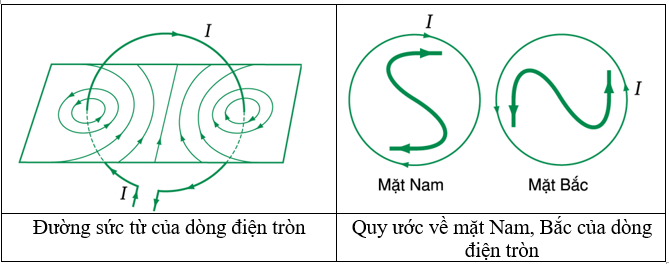
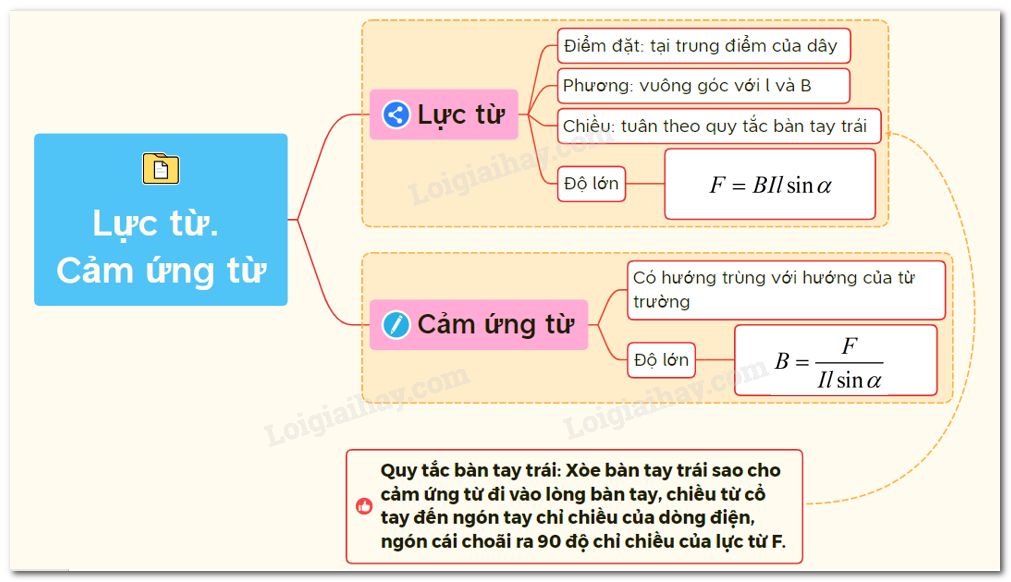
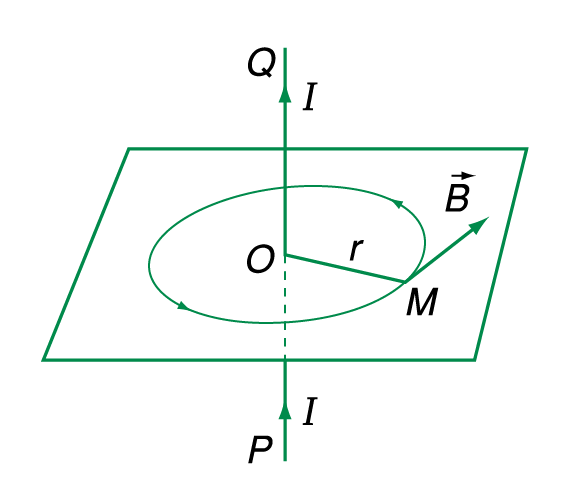
Chủ đề vecto cảm ứng từ vuông góc với mặt phẳng khung: Vecto cảm ứng từ vuông góc với mặt phẳng khung là một chủ đề quan trọng trong vật lý, với nhiều ứng dụng thực tiễn. Bài viết này cung cấp cái nhìn tổng quan về khái niệm, công thức tính toán và các ứng dụng của hiện tượng này, giúp bạn nắm vững kiến thức và áp dụng hiệu quả trong thực tế.
Mục lục
- Vecto Cảm Ứng Từ Vuông Góc Với Mặt Phẳng Khung: Khái Niệm và Ứng Dụng
- 1. Khái Niệm Vecto Cảm Ứng Từ
- 2. Điều Kiện Hình Thành Vecto Cảm Ứng Từ Vuông Góc Với Mặt Phẳng Khung
- 3. Công Thức Tính Toán Liên Quan
- 4. Ứng Dụng Của Vecto Cảm Ứng Từ Vuông Góc Với Mặt Phẳng Khung
- 5. Các Dạng Bài Tập Liên Quan
- 6. Phân Tích Các Lỗi Thường Gặp Và Cách Khắc Phục
- 7. Kết Luận
Vecto Cảm Ứng Từ Vuông Góc Với Mặt Phẳng Khung: Khái Niệm và Ứng Dụng
Vecto cảm ứng từ (\(\vec{B}\)) là một đại lượng vật lý quan trọng trong điện từ học, biểu thị cường độ và hướng của từ trường tại một điểm trong không gian. Khi vecto cảm ứng từ vuông góc với mặt phẳng khung dây dẫn, hiện tượng cảm ứng từ xảy ra, tạo ra dòng điện cảm ứng trong khung dây. Điều này dẫn đến nhiều ứng dụng trong các thiết bị điện và công nghiệp.
Điều Kiện Hình Thành
Khung dây dẫn phẳng phải có diện tích tiếp xúc với từ trường đều.
Vecto cảm ứng từ phải vuông góc với mặt phẳng khung dây, tức là góc giữa pháp tuyến của mặt phẳng khung và vecto cảm ứng từ là \(90^\circ\).
Công Thức Tính Suất Điện Động Cảm Ứng
Suất điện động cảm ứng \(e\) trong khung dây có thể được tính bằng công thức:
\[
e = \frac{\Delta \Phi}{\Delta t} = \frac{B \cdot S \cdot \cos(\alpha)}{\Delta t}
\]
Trong đó:
- \(B\) là độ lớn của vecto cảm ứng từ.
- \(S\) là diện tích mặt phẳng khung dây.
- \(\alpha\) là góc giữa vecto cảm ứng từ và pháp tuyến của mặt phẳng khung.
- \(\Delta t\) là khoảng thời gian từ thông thay đổi.
Ứng Dụng Trong Thực Tiễn
Hiện tượng vecto cảm ứng từ vuông góc với mặt phẳng khung có nhiều ứng dụng trong đời sống và kỹ thuật:
Máy phát điện: Khung dây quay trong từ trường đều để tạo ra suất điện động cảm ứng, chuyển đổi năng lượng cơ học thành điện năng.
Động cơ điện: Sử dụng lực từ để tạo chuyển động quay trong các thiết bị từ máy móc công nghiệp đến thiết bị gia dụng.
Cảm biến từ: Đo lường sự biến đổi của từ trường để phát hiện chuyển động hoặc thay đổi trong môi trường.
Thiết bị y tế: Máy chụp cộng hưởng từ (MRI) sử dụng từ trường mạnh để tạo ra hình ảnh chi tiết của cơ thể người.
Ví Dụ Minh Họa
Giả sử một khung dây dẫn phẳng có diện tích \(S = 0,06 \, m^2\) được đặt trong từ trường đều có vecto cảm ứng từ \(B = 0,5 \, T\) và góc \(\alpha = 0^\circ\). Khi đó, từ thông qua khung dây đạt giá trị lớn nhất và suất điện động cảm ứng có thể được tính như sau:
\[
\Phi = B \cdot S \cdot \cos(\alpha) = 0,5 \cdot 0,06 \cdot \cos(0^\circ) = 0,03 \, Wb
\]
Suất điện động cảm ứng trong khoảng thời gian \( \Delta t = 0,02 \, s \) là:
\[
e = \frac{\Delta \Phi}{\Delta t} = \frac{0,03}{0,02} = 1,5 \, V
\]
Kết Luận
Hiểu biết về vecto cảm ứng từ và các ứng dụng của nó giúp giải thích nhiều hiện tượng vật lý cũng như thiết kế và vận hành các thiết bị kỹ thuật hiện đại. Đây là một khía cạnh quan trọng trong việc nghiên cứu và áp dụng các nguyên lý vật lý vào đời sống.
.png)
1. Khái Niệm Vecto Cảm Ứng Từ
Vecto cảm ứng từ là một đại lượng vật lý biểu thị cường độ và hướng của từ trường tại một điểm cụ thể trong không gian. Khi một vật mang từ trường, ví dụ như một nam châm hay dòng điện, thì từ trường do nó tạo ra sẽ được mô tả bởi vecto cảm ứng từ.
Cảm ứng từ thường được ký hiệu là \( \mathbf{B} \) và là một vecto có cả độ lớn và hướng. Độ lớn của vecto cảm ứng từ tại một điểm thể hiện mức độ mạnh hay yếu của từ trường tại điểm đó, còn hướng của nó thể hiện phương mà lực từ tác dụng lên một hạt mang điện hoặc dòng điện tại điểm đó.
Để hiểu rõ hơn về khái niệm này, ta cần phân tích từ thông qua mặt phẳng khung dây. Nếu mặt phẳng khung dây vuông góc với vecto cảm ứng từ \( \mathbf{B} \), thì từ thông qua khung dây đạt giá trị lớn nhất và được tính theo công thức:
Trong đó:
- \( \Phi \): Từ thông qua khung dây (Weber, Wb)
- \( B \): Độ lớn của vecto cảm ứng từ (Tesla, T)
- \( S \): Diện tích mặt phẳng khung dây (m²)
Trường hợp vecto cảm ứng từ song song với mặt phẳng khung, từ thông bằng không, do đó lực từ không tạo ra momen quay trên khung. Ngược lại, khi vecto cảm ứng từ vuông góc với mặt phẳng khung, từ thông đạt cực đại, và các hiện tượng cảm ứng từ như suất điện động cảm ứng sẽ mạnh nhất.
2. Điều Kiện Hình Thành Vecto Cảm Ứng Từ Vuông Góc Với Mặt Phẳng Khung
Vecto cảm ứng từ vuông góc với mặt phẳng khung là một tình huống lý tưởng trong nhiều bài toán vật lý, đặc biệt là trong việc tính toán từ thông và momen từ. Để vecto cảm ứng từ hình thành theo hướng vuông góc với mặt phẳng khung, cần thỏa mãn các điều kiện sau:
- Từ Trường Đều:
Từ trường tạo ra bởi các nguồn từ như nam châm hoặc dòng điện phải là từ trường đều, nghĩa là vecto cảm ứng từ \( \mathbf{B} \) tại mọi điểm trong không gian đều có cùng độ lớn và cùng hướng. Trong trường hợp này, đường sức từ là những đường thẳng song song và cách đều nhau.
- Mặt Phẳng Khung Đặt Vuông Góc Với Đường Sức Từ:
Mặt phẳng của khung dây cần được đặt sao cho vuông góc với đường sức từ. Điều này có nghĩa là pháp tuyến của mặt phẳng khung (đường thẳng vuông góc với mặt phẳng khung tại điểm giao) phải song song với vecto cảm ứng từ \( \mathbf{B} \). Khi đó, góc \( \theta \) giữa pháp tuyến và vecto cảm ứng từ bằng 0 độ, và ta có:
\[ \Phi = B \cdot S \cdot \cos(0^\circ) = B \cdot S \]Trong đó, \( S \) là diện tích mặt phẳng khung.
- Độ Lớn Của Vecto Cảm Ứng Từ:
Độ lớn của \( \mathbf{B} \) phải đủ lớn để tạo ra một từ thông đáng kể qua khung dây. Giá trị này phụ thuộc vào nguồn từ trường và khoảng cách từ nguồn đến khung dây.
Khi các điều kiện trên được thỏa mãn, vecto cảm ứng từ sẽ hình thành vuông góc với mặt phẳng khung, dẫn đến việc từ thông qua khung đạt giá trị cực đại. Điều này cũng tạo điều kiện lý tưởng cho các hiện tượng cảm ứng từ như suất điện động cảm ứng và momen từ, thường được khai thác trong các thiết bị điện tử và máy phát điện.

3. Công Thức Tính Toán Liên Quan
Trong vật lý, khi vecto cảm ứng từ vuông góc với mặt phẳng khung, có một số công thức quan trọng liên quan đến từ thông, momen lực từ và suất điện động cảm ứng. Các công thức này giúp hiểu rõ hơn về hiện tượng cảm ứng từ và ứng dụng trong các bài toán thực tế.
- Công Thức Tính Từ Thông
Khi vecto cảm ứng từ \( \mathbf{B} \) vuông góc với mặt phẳng khung, từ thông \( \Phi \) qua khung dây được tính bằng:
\[ \Phi = B \cdot S \]Trong đó:
- \( B \): Độ lớn của vecto cảm ứng từ (Tesla, T)
- \( S \): Diện tích mặt phẳng khung (m²)
- Công Thức Suất Điện Động Cảm Ứng
Suất điện động cảm ứng \( \mathcal{E} \) trong khung dây khi từ thông biến thiên được tính theo định luật Faraday:
\[ \mathcal{E} = -\frac{d\Phi}{dt} \]Trong trường hợp đơn giản khi từ trường biến thiên đều, công thức trở thành:
\[ \mathcal{E} = -N \cdot \frac{\Delta B \cdot S}{\Delta t} \]Trong đó:
- \( N \): Số vòng dây trong khung
- \( \Delta B \): Độ biến thiên của vecto cảm ứng từ (T)
- \( \Delta t \): Thời gian từ trường biến thiên (s)
- Công Thức Tính Momen Lực Từ
Momen lực từ \( M \) tác dụng lên khung dây khi đặt trong từ trường đều được tính bằng:
\[ M = N \cdot B \cdot I \cdot S \cdot \sin\theta \]Trong đó:
- \( I \): Cường độ dòng điện trong khung dây (A)
- \( \theta \): Góc giữa vecto cảm ứng từ và pháp tuyến của mặt phẳng khung
Khi \( \theta = 90^\circ \), momen lực từ đạt giá trị lớn nhất:
\[ M_{\text{max}} = N \cdot B \cdot I \cdot S \]
Việc nắm vững các công thức này là nền tảng để giải quyết nhiều bài toán thực tiễn liên quan đến từ trường và ứng dụng trong các thiết bị điện từ.
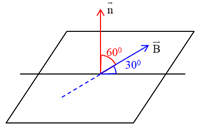
4. Ứng Dụng Của Vecto Cảm Ứng Từ Vuông Góc Với Mặt Phẳng Khung
Vecto cảm ứng từ vuông góc với mặt phẳng khung là một khái niệm cơ bản trong vật lý, có nhiều ứng dụng thực tiễn quan trọng trong công nghệ và đời sống hàng ngày. Dưới đây là một số ứng dụng nổi bật của hiện tượng này:
- Ứng Dụng Trong Động Cơ Điện:
Trong các động cơ điện, vecto cảm ứng từ vuông góc với mặt phẳng khung dây dẫn tạo ra momen lực, giúp rotor quay. Hiện tượng này là nền tảng cho việc hoạt động của các loại động cơ như động cơ DC và động cơ AC, trong đó từ trường được tạo ra bởi dòng điện chạy qua cuộn dây.
- Máy Phát Điện:
Máy phát điện hoạt động dựa trên nguyên lý cảm ứng điện từ, trong đó từ thông qua khung dây biến thiên khi rotor quay, tạo ra suất điện động cảm ứng. Ở đây, vecto cảm ứng từ vuông góc với mặt phẳng khung là điều kiện lý tưởng để tạo ra điện áp tối đa.
- Cảm Biến Từ Trường:
Các cảm biến từ trường như Hall sensor sử dụng nguyên lý cảm ứng từ để phát hiện sự thay đổi của từ trường xung quanh. Khi vecto cảm ứng từ vuông góc với mặt phẳng của cảm biến, tín hiệu cảm biến đạt giá trị lớn nhất, giúp phát hiện chính xác các vật thể kim loại hoặc từ tính.
- Ứng Dụng Trong Máy Gia Tốc Hạt:
Trong các máy gia tốc hạt, từ trường được sử dụng để điều khiển quỹ đạo của các hạt mang điện. Vecto cảm ứng từ vuông góc với mặt phẳng quỹ đạo hạt giúp duy trì quỹ đạo chuyển động ổn định của hạt, đảm bảo quá trình gia tốc hiệu quả.
- Ứng Dụng Trong Các Thiết Bị Điện Tử:
Nhiều thiết bị điện tử, như máy đo từ trường và từ kế, hoạt động dựa trên nguyên lý cảm ứng từ. Đặc biệt, khi vecto cảm ứng từ vuông góc với mặt phẳng của cuộn dây trong thiết bị, nó sẽ tạo ra tín hiệu điện mạnh, cho phép đo lường và kiểm soát từ trường một cách chính xác.
Những ứng dụng trên cho thấy tầm quan trọng của vecto cảm ứng từ vuông góc với mặt phẳng khung trong nhiều lĩnh vực, từ công nghiệp đến đời sống hàng ngày, và đóng góp không nhỏ vào sự phát triển của công nghệ hiện đại.

5. Các Dạng Bài Tập Liên Quan
Vecto cảm ứng từ vuông góc với mặt phẳng khung là một chủ đề thường gặp trong các bài tập vật lý. Các bài tập liên quan thường được chia thành nhiều dạng khác nhau, từ cơ bản đến nâng cao, giúp học sinh nắm vững khái niệm và áp dụng trong thực tế.
- Dạng 1: Tính Từ Thông Qua Khung Dây
Ở dạng bài này, học sinh cần tính từ thông \( \Phi \) qua khung dây khi biết độ lớn của vecto cảm ứng từ \( B \) và diện tích khung \( S \). Các bài toán có thể yêu cầu tính từ thông trong các trường hợp vecto cảm ứng từ vuông góc hoặc không vuông góc với mặt phẳng khung:
\[ \Phi = B \cdot S \cdot \cos\theta \]Trong đó, \( \theta \) là góc giữa vecto cảm ứng từ và pháp tuyến của mặt phẳng khung.
- Dạng 2: Tính Suất Điện Động Cảm Ứng
Bài toán dạng này thường yêu cầu tính suất điện động cảm ứng \( \mathcal{E} \) trong khung dây khi từ thông thay đổi theo thời gian. Công thức Faraday là công cụ chính để giải quyết dạng bài này:
\[ \mathcal{E} = -\frac{d\Phi}{dt} \]Bài toán có thể yêu cầu tính \( \mathcal{E} \) trong các trường hợp từ thông thay đổi đều hoặc không đều.
- Dạng 3: Tính Momen Lực Từ Tác Dụng Lên Khung Dây
Học sinh cần xác định momen lực từ \( M \) tác dụng lên khung dây khi đặt trong từ trường đều. Bài toán sẽ cho biết dòng điện \( I \), diện tích khung dây \( S \), và độ lớn của vecto cảm ứng từ \( B \). Công thức tính momen lực từ là:
\[ M = N \cdot B \cdot I \cdot S \cdot \sin\theta \]Dạng bài này thường xuất hiện trong các đề thi với nhiều biến đổi và tình huống khác nhau.
- Dạng 4: Phân Tích Hiện Tượng Cảm Ứng Từ Trong Thực Tế
Những bài toán này yêu cầu học sinh phân tích hiện tượng cảm ứng từ trong các thiết bị thực tế như động cơ điện, máy phát điện, hoặc các thiết bị cảm biến từ. Bài toán đòi hỏi hiểu biết sâu về cách thức hoạt động của các thiết bị và khả năng áp dụng các công thức đã học để giải thích các hiện tượng quan sát được.
Thông qua việc giải các dạng bài tập trên, học sinh sẽ có cái nhìn tổng quát và sâu sắc hơn về các khái niệm liên quan đến vecto cảm ứng từ và các ứng dụng trong đời sống thực tế.
XEM THÊM:
6. Phân Tích Các Lỗi Thường Gặp Và Cách Khắc Phục
Trong quá trình học và làm bài tập về vecto cảm ứng từ vuông góc với mặt phẳng khung, học sinh thường mắc phải một số lỗi phổ biến. Dưới đây là phân tích chi tiết các lỗi này và cách khắc phục để đạt kết quả tốt nhất:
- Lỗi 1: Nhầm Lẫn Giữa Góc Vuông Và Góc Khác
Một lỗi thường gặp là học sinh nhầm lẫn giữa góc vuông (90°) và các góc khác khi xác định góc giữa vecto cảm ứng từ và mặt phẳng khung. Điều này dẫn đến việc tính sai từ thông hoặc momen lực từ.
Cách Khắc Phục: Luôn kiểm tra kỹ góc giữa vecto cảm ứng từ và mặt phẳng khung. Sử dụng hình vẽ minh họa và công cụ đo góc nếu cần để đảm bảo chính xác.
- Lỗi 2: Tính Sai Diện Tích Mặt Phẳng Khung
Khi tính từ thông, nhiều học sinh có thể tính sai diện tích mặt phẳng khung do nhầm lẫn công thức hoặc đơn vị đo lường.
Cách Khắc Phục: Nhớ lại công thức tính diện tích phù hợp với hình dạng của khung (ví dụ: hình vuông, hình tròn) và đảm bảo rằng tất cả các đơn vị đo lường đều nhất quán.
- Lỗi 3: Sử Dụng Sai Công Thức Suất Điện Động Cảm Ứng
Nhiều học sinh mắc lỗi khi áp dụng công thức suất điện động cảm ứng, đặc biệt trong các trường hợp từ thông thay đổi không đều.
Cách Khắc Phục: Xác định rõ tình huống bài toán, từ đó chọn công thức phù hợp. Đối với từ thông thay đổi không đều, hãy sử dụng công thức tổng quát \(\mathcal{E} = -\frac{d\Phi}{dt}\) thay vì công thức đơn giản hóa.
- Lỗi 4: Không Xác Định Đúng Phương Chiều Của Vecto Cảm Ứng Từ
Khi giải bài tập liên quan đến momen lực từ, việc xác định sai phương chiều của vecto cảm ứng từ dẫn đến kết quả sai.
Cách Khắc Phục: Sử dụng quy tắc bàn tay phải để xác định đúng phương chiều của vecto cảm ứng từ và lực từ. Luyện tập qua nhiều ví dụ khác nhau để quen thuộc với quy tắc này.
- Lỗi 5: Thiếu Sót Khi Phân Tích Hiện Tượng Cảm Ứng Từ
Trong các bài tập ứng dụng, học sinh có thể bỏ qua một số yếu tố quan trọng như điện trở của cuộn dây hoặc sự thay đổi nhiệt độ ảnh hưởng đến từ thông.
Cách Khắc Phục: Đọc kỹ đề bài và ghi chú lại tất cả các yếu tố có thể ảnh hưởng đến kết quả. Nếu cần thiết, làm rõ những giả thiết của bài toán trước khi bắt đầu giải.
Việc nắm rõ các lỗi thường gặp và phương pháp khắc phục sẽ giúp học sinh cải thiện kỹ năng giải bài tập liên quan đến vecto cảm ứng từ và đạt được kết quả cao hơn trong các kỳ thi.

7. Kết Luận
Vecto cảm ứng từ vuông góc với mặt phẳng khung là một khái niệm quan trọng trong vật lý, đặc biệt trong các bài toán liên quan đến từ trường và điện từ. Qua các phần trước, chúng ta đã tìm hiểu về khái niệm cơ bản, điều kiện hình thành, công thức tính toán, và các ứng dụng thực tế. Đồng thời, những lỗi thường gặp và cách khắc phục đã được phân tích chi tiết, giúp người học tránh được những sai sót phổ biến trong quá trình giải bài tập.
Tổng kết lại, việc nắm vững các kiến thức về vecto cảm ứng từ không chỉ giúp cải thiện kỹ năng giải toán mà còn mang lại những hiểu biết sâu sắc về các hiện tượng điện từ trong thực tế. Hy vọng rằng, với những kiến thức và kỹ năng đã được cung cấp, bạn đọc sẽ tự tin hơn trong việc tiếp cận và giải quyết các bài toán liên quan, đồng thời áp dụng chúng hiệu quả trong các tình huống thực tế.