Chủ đề lý 12 lượng tử ánh sáng: Lý 12 lượng tử ánh sáng là một phần quan trọng trong chương trình Vật Lý trung học phổ thông, giúp học sinh nắm vững kiến thức về bản chất của ánh sáng và các hiện tượng liên quan. Bài viết này sẽ cung cấp một cái nhìn tổng quan, chi tiết và ứng dụng thực tế của thuyết lượng tử ánh sáng trong đời sống.
Mục lục
Lý Thuyết Lượng Tử Ánh Sáng Trong Vật Lý Lớp 12
Trong chương trình Vật Lý lớp 12, thuyết lượng tử ánh sáng là một chủ đề quan trọng, giúp học sinh hiểu về bản chất của ánh sáng, sự tương tác của ánh sáng với vật chất và các hiện tượng liên quan. Đây là nội dung thuộc chương trình giáo dục trung học phổ thông, cụ thể bao gồm các phần sau:
1. Hiện Tượng Quang Điện
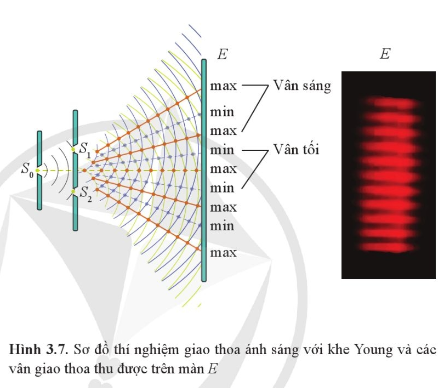
Hiện tượng quang điện là hiện tượng ánh sáng chiếu vào bề mặt kim loại làm bật các electron ra khỏi mặt kim loại. Đây là bằng chứng thực nghiệm quan trọng giúp phát triển thuyết lượng tử ánh sáng.
- Khi ánh sáng có bước sóng nhỏ hơn hoặc bằng giới hạn quang điện của một kim loại, hiện tượng quang điện sẽ xảy ra.
- Điện thế hãm và cường độ dòng quang điện bão hòa là hai đại lượng quan trọng trong việc mô tả hiện tượng quang điện.
2. Thuyết Lượng Tử Ánh Sáng
Thuyết lượng tử ánh sáng được Einstein đề xuất, dựa trên giả thuyết của Planck. Theo thuyết này, ánh sáng không chỉ có tính chất sóng mà còn có tính chất hạt. Các hạt ánh sáng này gọi là photon.
- Photon có năng lượng xác định bởi công thức: \[E = hf\] với \(h\) là hằng số Planck và \(f\) là tần số của ánh sáng.
- Các photon di chuyển với vận tốc ánh sáng và có thể tương tác với các electron trong kim loại, gây ra hiện tượng quang điện.
3. Các Định Luật Quang Điện
- Định luật thứ nhất: Ánh sáng phải có bước sóng ngắn hơn giới hạn quang điện của kim loại mới gây ra được hiện tượng quang điện.
- Định luật thứ hai: Cường độ dòng quang điện bão hòa tỉ lệ thuận với cường độ bức xạ kích thích.
- Định luật thứ ba: Động năng cực đại của electron không phụ thuộc vào cường độ ánh sáng mà phụ thuộc vào bước sóng của ánh sáng.
4. Ứng Dụng Của Thuyết Lượng Tử Ánh Sáng
Thuyết lượng tử ánh sáng có nhiều ứng dụng trong đời sống và công nghệ hiện đại:
- Các thiết bị cảm biến ánh sáng và camera kỹ thuật số sử dụng nguyên lý quang điện.
- Công nghệ laser và các thiết bị liên quan như máy quang phổ, máy in laser đều dựa trên cơ sở của thuyết lượng tử ánh sáng.
5. Bài Tập Thực Hành
Để củng cố kiến thức, học sinh thường làm các bài tập liên quan đến tính toán năng lượng photon, xác định bước sóng giới hạn và giải quyết các bài toán về hiện tượng quang điện. Ví dụ:
- Tính năng lượng của một photon có tần số \(f = 6 \times 10^{14} \, \text{Hz}\).
- Xác định bước sóng giới hạn của một kim loại có công thoát \(\phi = 2 \, \text{eV}\).
Như vậy, chương lượng tử ánh sáng trong Vật Lý lớp 12 không chỉ giúp học sinh hiểu sâu hơn về bản chất của ánh sáng mà còn trang bị những kiến thức cần thiết cho việc ứng dụng khoa học vào thực tiễn.

.png)
1. Giới thiệu về Lượng Tử Ánh Sáng
Lượng tử ánh sáng là một khái niệm quan trọng trong vật lý hiện đại, được phát triển từ những nghiên cứu của các nhà khoa học như Max Planck và Albert Einstein. Đây là nền tảng giúp giải thích các hiện tượng liên quan đến ánh sáng mà lý thuyết sóng ánh sáng truyền thống không thể làm rõ.
Theo thuyết lượng tử, ánh sáng không chỉ tồn tại dưới dạng sóng mà còn có tính chất hạt. Các hạt ánh sáng này được gọi là photon. Mỗi photon mang một lượng năng lượng xác định, được mô tả bởi công thức:
\[
E = hf
\]
Trong đó:
- \(E\) là năng lượng của photon (đơn vị Joule).
- \(h\) là hằng số Planck, có giá trị \(h = 6.626 \times 10^{-34} \, \text{J} \cdot \text{s}\).
- \(f\) là tần số của ánh sáng (đơn vị Hz).
Lý thuyết lượng tử ánh sáng ra đời từ những thí nghiệm về hiện tượng quang điện, trong đó ánh sáng chiếu vào một bề mặt kim loại làm bật các electron ra khỏi mặt kim loại. Hiện tượng này chỉ có thể được giải thích bằng việc coi ánh sáng như các hạt photon, với mỗi photon cung cấp đủ năng lượng để giải phóng một electron khỏi kim loại.
Lượng tử ánh sáng không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tế, từ công nghệ laser, cảm biến quang điện đến các thiết bị viễn thông và năng lượng tái tạo. Việc hiểu rõ bản chất của lượng tử ánh sáng là nền tảng để tiếp cận những công nghệ tiên tiến trong thế giới hiện đại.
2. Hiện Tượng Quang Điện
Hiện tượng quang điện là một trong những hiện tượng quan trọng minh chứng cho bản chất lượng tử của ánh sáng. Hiện tượng này được quan sát khi ánh sáng chiếu vào bề mặt của một kim loại và làm bật các electron ra khỏi bề mặt đó. Đây là bằng chứng thực nghiệm cho thấy ánh sáng có thể thể hiện tính chất hạt (photon).
Quá trình của hiện tượng quang điện diễn ra như sau:
- Khi ánh sáng có bước sóng đủ nhỏ (tức là có năng lượng photon lớn) chiếu vào bề mặt kim loại, năng lượng của photon sẽ được truyền cho các electron trong kim loại.
- Nếu năng lượng photon đủ lớn để thắng lực liên kết của electron với kim loại (công thoát), electron sẽ bị giải phóng khỏi bề mặt kim loại, tạo ra dòng electron gọi là dòng quang điện.
- Năng lượng của photon được mô tả bởi công thức: \[E = hf\], trong đó \(E\) là năng lượng của photon, \(h\) là hằng số Planck, và \(f\) là tần số của ánh sáng.
- Nếu năng lượng photon nhỏ hơn công thoát, hiện tượng quang điện sẽ không xảy ra, dù cường độ ánh sáng có mạnh đến đâu.
Hiện tượng quang điện có thể được tóm tắt bằng ba định luật quang điện cơ bản:
- Định luật 1: Hiện tượng quang điện chỉ xảy ra khi ánh sáng có bước sóng nhỏ hơn hoặc bằng giới hạn quang điện của kim loại.
- Định luật 2: Cường độ dòng quang điện tỉ lệ thuận với cường độ của chùm ánh sáng chiếu vào.
- Định luật 3: Động năng cực đại của các electron quang điện không phụ thuộc vào cường độ ánh sáng mà chỉ phụ thuộc vào tần số của ánh sáng.
Hiện tượng quang điện có nhiều ứng dụng trong thực tiễn, chẳng hạn như trong các thiết bị cảm biến ánh sáng, tế bào quang điện, và trong việc nghiên cứu các tính chất của vật liệu. Hiểu rõ hiện tượng này giúp củng cố kiến thức về bản chất lượng tử của ánh sáng và mối quan hệ giữa ánh sáng và vật chất.

3. Thuyết Lượng Tử Ánh Sáng của Einstein
Thuyết Lượng Tử Ánh Sáng của Einstein, hay còn gọi là lý thuyết photon, được phát triển để giải thích các hiện tượng mà thuyết sóng ánh sáng truyền thống không thể giải thích. Albert Einstein đã mở rộng và hoàn thiện lý thuyết này dựa trên giả thuyết của Max Planck về lượng tử năng lượng. Theo Einstein, ánh sáng không chỉ là sóng mà còn có tính chất hạt, tức là ánh sáng bao gồm các hạt gọi là photon.
3.1. Giả thuyết của Planck và sự phát triển của Einstein
Giả thuyết của Max Planck về lượng tử năng lượng cho rằng năng lượng của các dao động của các hạt vật chất trong các vật đen phát ra là rời rạc và tỷ lệ với tần số của chúng:
\(E = h \cdot f\)
Trong đó:
- \(E\) là năng lượng của một lượng tử ánh sáng (photon)
- \(h\) là hằng số Planck (\(h \approx 6.626 \times 10^{-34}\) J·s)
- \(f\) là tần số của ánh sáng
Albert Einstein đã áp dụng lý thuyết này vào việc giải thích hiện tượng quang điện, đề xuất rằng ánh sáng thực chất bao gồm các hạt năng lượng nhỏ (photon). Khi một photon có đủ năng lượng, nó có thể giải phóng một electron từ bề mặt kim loại, tạo ra hiện tượng quang điện.
3.2. Định luật về Giới Hạn Quang Điện
Einstein cũng đưa ra một định luật quan trọng liên quan đến giới hạn quang điện, khẳng định rằng:
\(hf = A + \frac{1}{2}mv^2\)
Trong đó:
- \(hf\) là năng lượng của photon ánh sáng
- \(A\) là công thoát, năng lượng tối thiểu để giải phóng một electron khỏi kim loại
- \(m\) là khối lượng của electron
- \(v\) là vận tốc của electron sau khi bị giải phóng
Định luật này cho thấy năng lượng của một photon ánh sáng phải lớn hơn hoặc bằng công thoát thì mới có thể gây ra hiện tượng quang điện. Khi năng lượng photon lớn hơn công thoát, phần năng lượng dư sẽ chuyển thành động năng của electron bị giải phóng.
3.3. Các công thức và hệ quả của Thuyết Lượng Tử Ánh Sáng
Thuyết Lượng Tử Ánh Sáng của Einstein đã đưa ra nhiều công thức quan trọng và các hệ quả ứng dụng thực tế:
- Công thức năng lượng photon: \(E = h \cdot f = \frac{hc}{\lambda}\)
- Công thức giới hạn bước sóng: \(\lambda_0 = \frac{hc}{A}\)
- Hệ quả về tính chất hạt của ánh sáng: Ánh sáng có thể được xem như một dòng các hạt photon, và mỗi photon mang một lượng tử năng lượng tương ứng với tần số ánh sáng.
- Ứng dụng trong công nghệ: Thuyết lượng tử ánh sáng là nền tảng cho sự phát triển của các công nghệ như pin mặt trời, cảm biến ánh sáng, và laser.
Thuyết Lượng Tử Ánh Sáng của Einstein không chỉ giải thích rõ ràng hiện tượng quang điện mà còn mở ra những hướng nghiên cứu mới trong vật lý hiện đại, đóng góp quan trọng vào sự phát triển của cơ học lượng tử và các công nghệ hiện đại.
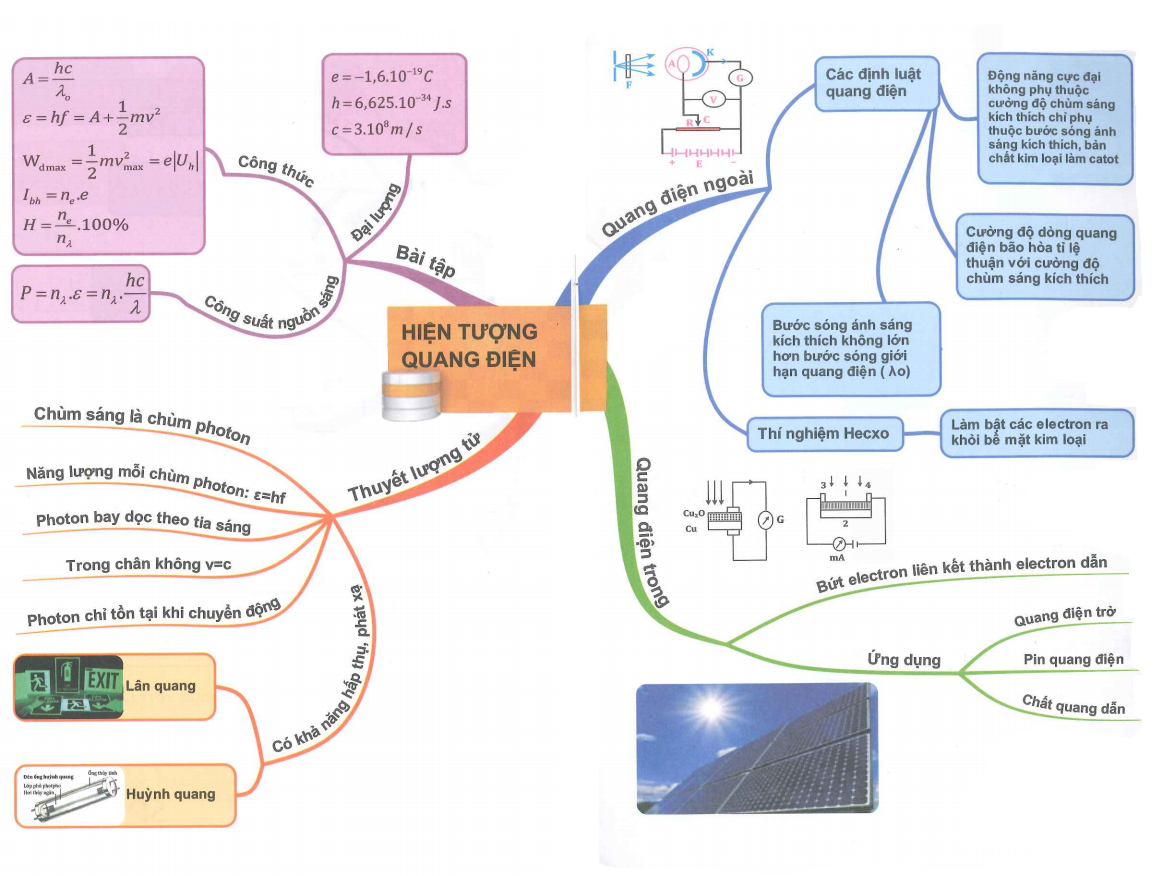
4. Các Định Luật Cơ Bản Liên Quan Đến Lượng Tử Ánh Sáng
Các định luật cơ bản liên quan đến lượng tử ánh sáng là những nguyên lý quan trọng giúp giải thích các hiện tượng quang học và điện từ liên quan đến ánh sáng. Những định luật này là nền tảng cho sự phát triển của cơ học lượng tử và nhiều ứng dụng thực tế trong công nghệ hiện đại.
4.1. Định luật bảo toàn năng lượng trong Hiện Tượng Quang Điện
Định luật bảo toàn năng lượng là một trong những định luật cơ bản nhất của vật lý và cũng áp dụng cho hiện tượng quang điện. Khi một photon ánh sáng chiếu vào bề mặt kim loại, năng lượng của nó được truyền cho electron. Nếu năng lượng này đủ lớn, electron sẽ thoát ra khỏi bề mặt kim loại. Phương trình của định luật bảo toàn năng lượng trong hiện tượng quang điện được biểu diễn như sau:
\(E_{photon} = A + \frac{1}{2}mv^2\)
Trong đó:
- \(E_{photon} = h \cdot f\): Năng lượng của photon
- \(A\): Công thoát, năng lượng tối thiểu để electron thoát khỏi bề mặt kim loại
- \(m\): Khối lượng của electron
- \(v\): Vận tốc của electron khi thoát ra khỏi bề mặt kim loại
Định luật này cho thấy rằng năng lượng của photon được chia thành công thoát và động năng của electron. Nếu năng lượng của photon nhỏ hơn công thoát, hiện tượng quang điện sẽ không xảy ra.
4.2. Định luật về cường độ dòng quang điện bão hòa
Định luật về cường độ dòng quang điện bão hòa cho biết khi ánh sáng có tần số và cường độ đủ lớn chiếu vào một bề mặt kim loại, dòng quang điện đạt đến trạng thái bão hòa. Điều này có nghĩa là tất cả các electron có khả năng thoát ra đã được phát xạ. Cường độ dòng quang điện bão hòa phụ thuộc vào cường độ ánh sáng chiếu vào và không phụ thuộc vào tần số của ánh sáng, miễn là tần số đó lớn hơn giá trị ngưỡng:
\(I_{max} \propto P\)
Trong đó:
- \(I_{max}\): Cường độ dòng quang điện bão hòa
- \(P\): Cường độ của ánh sáng chiếu tới
Định luật này cho thấy rằng khi tăng cường độ ánh sáng chiếu tới (tăng số lượng photon chiếu tới), số electron thoát ra cũng tăng, do đó cường độ dòng quang điện tăng lên cho đến khi đạt tới giá trị bão hòa.
4.3. Định luật về động năng cực đại của electron
Động năng cực đại của electron thoát ra khỏi bề mặt kim loại trong hiện tượng quang điện được xác định bởi năng lượng của photon và công thoát của kim loại. Định luật này cho thấy mối quan hệ giữa động năng cực đại của electron và tần số của ánh sáng chiếu vào:
\(K_{max} = h \cdot f - A\)
Trong đó:
- \(K_{max} = \frac{1}{2}mv^2_{max}\): Động năng cực đại của electron
- \(h\): Hằng số Planck
- \(f\): Tần số của ánh sáng chiếu tới
- \(A\): Công thoát của kim loại
Định luật này cho thấy rằng động năng cực đại của electron phụ thuộc tuyến tính vào tần số ánh sáng chiếu tới. Khi tần số tăng, động năng cực đại của electron cũng tăng, và ngược lại. Nếu tần số ánh sáng chiếu vào nhỏ hơn giá trị ngưỡng, không có electron nào có đủ năng lượng để thoát ra, và do đó không có hiện tượng quang điện xảy ra.
Các định luật cơ bản này không chỉ giải thích các hiện tượng quang học mà còn là cơ sở cho sự phát triển của nhiều ứng dụng công nghệ như cảm biến ánh sáng, pin mặt trời, và các thiết bị đo lường quang học hiện đại.

5. Bài Tập và Câu Hỏi Thực Hành
Để hiểu rõ hơn về các khái niệm và định luật liên quan đến Lượng Tử Ánh Sáng, chúng ta cần thực hành qua các bài tập và câu hỏi. Dưới đây là một số bài tập và câu hỏi thực hành để củng cố kiến thức.
5.1. Bài tập tính toán năng lượng của photon
Cho biết tần số của ánh sáng là \(f = 5 \times 10^{14}\) Hz. Hãy tính năng lượng của một photon.
Hướng dẫn: Sử dụng công thức:
\(E = h \cdot f\)
- Trong đó \(h = 6.626 \times 10^{-34}\) J·s (hằng số Planck)
- \(f = 5 \times 10^{14}\) Hz là tần số của ánh sáng
Lời giải:
Năng lượng của photon:
\(E = 6.626 \times 10^{-34} \times 5 \times 10^{14} = 3.313 \times 10^{-19}\) J
5.2. Bài tập về bước sóng giới hạn
Một kim loại có công thoát là \(A = 4 \times 10^{-19}\) J. Tìm bước sóng giới hạn \(\lambda_0\) của ánh sáng để có thể gây ra hiện tượng quang điện.
Hướng dẫn: Sử dụng công thức:
\(\lambda_0 = \frac{hc}{A}\)
- Trong đó \(h = 6.626 \times 10^{-34}\) J·s, \(c = 3 \times 10^8\) m/s
- \(A = 4 \times 10^{-19}\) J là công thoát
Lời giải:
Bước sóng giới hạn:
\(\lambda_0 = \frac{6.626 \times 10^{-34} \times 3 \times 10^8}{4 \times 10^{-19}} = 4.97 \times 10^{-7}\) m
\(\lambda_0 = 497\) nm
5.3. Bài tập về Hiện Tượng Quang Điện
Một ánh sáng có bước sóng \(\lambda = 450\) nm chiếu vào một bề mặt kim loại có công thoát \(A = 2.5 \times 10^{-19}\) J. Hãy tính động năng cực đại của electron thoát ra từ bề mặt kim loại.
Hướng dẫn: Sử dụng công thức:
\(K_{max} = \frac{hc}{\lambda} - A\)
- \(h = 6.626 \times 10^{-34}\) J·s
- \(c = 3 \times 10^8\) m/s
- \(\lambda = 450 \times 10^{-9}\) m
- \(A = 2.5 \times 10^{-19}\) J
Lời giải:
Tính năng lượng của photon:
\(E = \frac{6.626 \times 10^{-34} \times 3 \times 10^8}{450 \times 10^{-9}} = 4.42 \times 10^{-19}\) J
Động năng cực đại của electron:
\(K_{max} = 4.42 \times 10^{-19} - 2.5 \times 10^{-19} = 1.92 \times 10^{-19}\) J
5.4. Câu hỏi trắc nghiệm
- Năng lượng của một photon có tần số \(f = 6 \times 10^{14}\) Hz là bao nhiêu?
- A. \(2.48 \times 10^{-19}\) J
- B. \(3.97 \times 10^{-19}\) J
- C. \(4.0 \times 10^{-19}\) J
- D. \(3.98 \times 10^{-19}\) J
- Bước sóng giới hạn của ánh sáng có thể gây ra hiện tượng quang điện với công thoát \(A = 5 \times 10^{-19}\) J là bao nhiêu?
- A. \(200\) nm
- B. \(300\) nm
- C. \(400\) nm
- D. \(500\) nm
Hãy cố gắng giải các bài tập và câu hỏi trắc nghiệm trên để củng cố kiến thức về Lượng Tử Ánh Sáng và chuẩn bị tốt cho các kỳ thi sắp tới.
XEM THÊM:
6. Ứng Dụng Thực Tế của Thuyết Lượng Tử Ánh Sáng
Thuyết lượng tử ánh sáng đã mở ra nhiều hướng nghiên cứu và ứng dụng mới trong khoa học và công nghệ. Các ứng dụng thực tế của thuyết này đã góp phần quan trọng vào sự phát triển của nhiều lĩnh vực, từ y học, công nghệ thông tin đến năng lượng tái tạo và viễn thông.
6.1. Ứng dụng trong công nghệ laser
Công nghệ laser là một trong những ứng dụng quan trọng nhất của thuyết lượng tử ánh sáng. Laser (Light Amplification by Stimulated Emission of Radiation) hoạt động dựa trên nguyên lý của hiện tượng phát xạ kích thích, một khái niệm cốt lõi trong cơ học lượng tử. Các bước sóng cụ thể được khuếch đại để tạo ra chùm tia sáng đồng nhất với năng lượng cao và độ chính xác tuyệt đối. Ứng dụng của laser rất đa dạng, bao gồm:
- Y học: Laser được sử dụng trong phẫu thuật, điều trị mắt, và các liệu pháp chữa trị không xâm lấn khác.
- Công nghiệp: Cắt, hàn kim loại, và khắc laser trên nhiều chất liệu.
- Viễn thông: Laser được sử dụng để truyền tín hiệu trong cáp quang với tốc độ cao và ít suy hao.
6.2. Ứng dụng trong cảm biến ánh sáng
Cảm biến ánh sáng, hay còn gọi là quang điện trở, hoạt động dựa trên hiệu ứng quang điện - một khái niệm quan trọng trong thuyết lượng tử ánh sáng. Khi ánh sáng chiếu vào cảm biến, các photon sẽ tương tác với các electron trong vật liệu, giải phóng chúng và tạo ra dòng điện. Ứng dụng của cảm biến ánh sáng bao gồm:
- Camera và máy ảnh: Cảm biến CMOS và CCD sử dụng trong máy ảnh và camera số để thu nhận hình ảnh.
- Thiết bị tự động hóa: Cảm biến ánh sáng được sử dụng trong các thiết bị tự động hóa để phát hiện chuyển động, đo mức độ ánh sáng và điều chỉnh ánh sáng trong môi trường.
- Các thiết bị an ninh: Cảm biến ánh sáng được sử dụng trong hệ thống báo động và bảo mật để phát hiện sự hiện diện của người hoặc vật thể.
6.3. Ứng dụng trong ngành năng lượng tái tạo
Thuyết lượng tử ánh sáng cũng đóng vai trò quan trọng trong ngành năng lượng tái tạo, đặc biệt là trong việc phát triển pin mặt trời (solar cells). Hiệu ứng quang điện được áp dụng để chuyển đổi năng lượng ánh sáng thành điện năng một cách trực tiếp. Đây là một phương pháp bền vững và thân thiện với môi trường để sản xuất điện. Các ứng dụng cụ thể bao gồm:
- Tấm pin mặt trời: Các tấm pin mặt trời trên mái nhà và các công trình kiến trúc sử dụng để cung cấp điện cho các thiết bị và hệ thống điện.
- Trạm năng lượng mặt trời: Các trạm năng lượng mặt trời quy mô lớn được sử dụng để cung cấp điện cho các khu vực đô thị và công nghiệp.
- Thiết bị điện tử di động: Nhiều thiết bị di động và đồng hồ thông minh sử dụng pin mặt trời nhỏ để kéo dài thời gian sử dụng mà không cần sạc pin thường xuyên.
Những ứng dụng này chứng minh sức mạnh của thuyết lượng tử ánh sáng trong việc giải thích các hiện tượng tự nhiên và phát triển các công nghệ tiên tiến. Qua đó, chúng ta có thể thấy rõ vai trò quan trọng của thuyết lượng tử ánh sáng trong đời sống hàng ngày và công nghệ hiện đại.