Chủ đề giải bài tập sóng ánh sáng: Bài viết này cung cấp hướng dẫn chi tiết về lý thuyết sóng ánh sáng và cách giải các bài tập liên quan. Khám phá các phương pháp giải bài tập sóng ánh sáng cùng với các ví dụ minh họa để củng cố kiến thức của bạn.
Mục lục
Giải bài tập sóng ánh sáng
Bài viết này tổng hợp các kiến thức và bài tập về sóng ánh sáng, một chủ đề quan trọng trong chương trình vật lý phổ thông. Bạn sẽ tìm thấy các lý thuyết cơ bản, phương pháp giải bài tập, cũng như các bài tập tự luyện về giao thoa, nhiễu xạ ánh sáng, và các hiện tượng liên quan.
Lý thuyết cơ bản về sóng ánh sáng
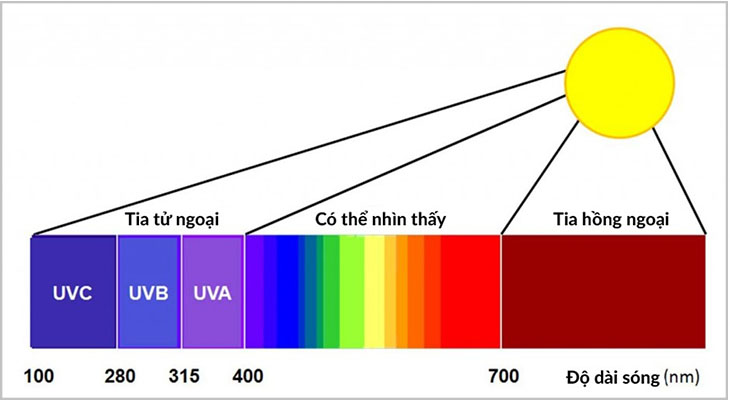
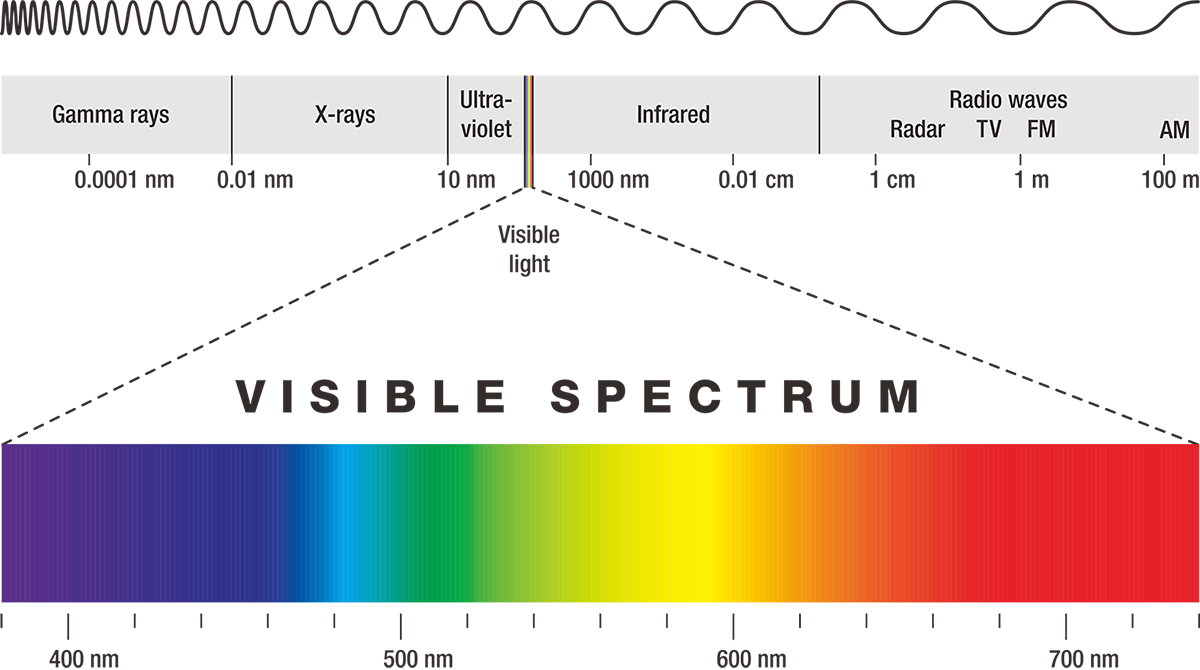
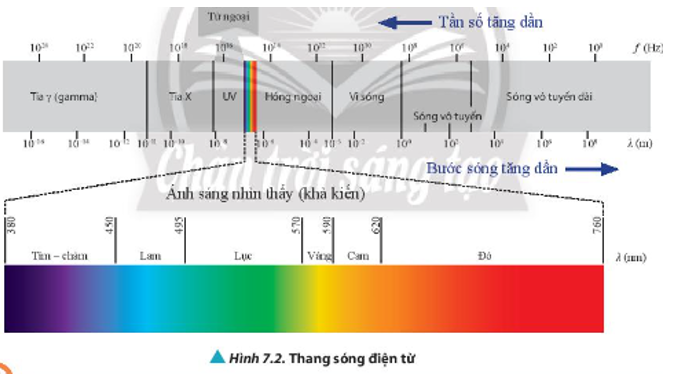
Sóng ánh sáng là sóng điện từ, có bước sóng trong khoảng từ 400 nm đến 700 nm tương ứng với dải màu từ tím đến đỏ. Sóng ánh sáng có thể gây ra các hiện tượng như giao thoa, nhiễu xạ, và tán sắc.
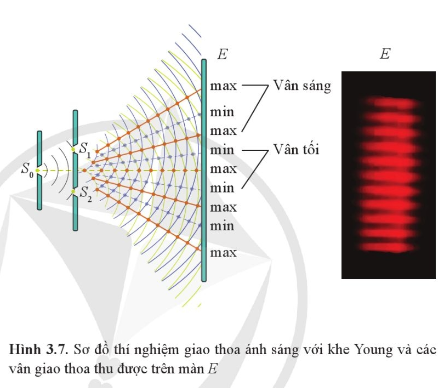
- Giao thoa ánh sáng: Khi hai hay nhiều sóng ánh sáng gặp nhau, chúng có thể tạo ra các vân sáng và vân tối do sự chồng chập của các sóng. Hiện tượng này chứng tỏ ánh sáng có tính chất sóng.
- Nhiễu xạ ánh sáng: Là hiện tượng ánh sáng bị bẻ cong khi đi qua các khe hẹp hoặc cạnh của vật cản. Điều này cũng cho thấy tính chất sóng của ánh sáng.
- Tán sắc ánh sáng: Khi ánh sáng trắng đi qua lăng kính, nó bị phân tách thành các màu thành phần. Hiện tượng này là do sự thay đổi chiết suất của các bước sóng khác nhau trong môi trường.
Phương pháp giải bài tập sóng ánh sáng
Để giải các bài tập về sóng ánh sáng, bạn cần nắm vững các công thức và nguyên lý cơ bản. Dưới đây là một số phương pháp thường gặp:
- Sử dụng công thức bước sóng \( \lambda = \frac{v}{f} \), trong đó \( v \) là vận tốc sóng trong môi trường, và \( f \) là tần số sóng.
- Áp dụng công thức giao thoa \( \Delta x = \frac{\lambda D}{a} \), với \( \Delta x \) là khoảng cách giữa các vân, \( D \) là khoảng cách từ màn đến khe, và \( a \) là khoảng cách giữa hai khe.
- Giải các bài toán nhiễu xạ bằng công thức \( d\sin\theta = k\lambda \) cho các vân sáng bậc k, trong đó \( d \) là khoảng cách giữa các khe, \( \theta \) là góc nhiễu xạ.
Bài tập tự luyện về sóng ánh sáng
| Bài tập 1: | Cho bước sóng của ánh sáng đỏ trong không khí là \( \lambda_0 = 700 \, \text{nm} \). Tính bước sóng của nó khi truyền trong nước có chiết suất \( n = 1,33 \). |
| Đáp án: | Sử dụng công thức \( \lambda = \frac{\lambda_0}{n} = \frac{700}{1,33} \approx 526 \, \text{nm} \). |
| Bài tập 2: | Hai khe cách nhau \( a = 0,5 \, \text{mm} \), chiếu ánh sáng đơn sắc có bước sóng \( \lambda = 600 \, \text{nm} \). Tìm khoảng cách giữa các vân giao thoa trên màn cách khe \( D = 2 \, \text{m} \). |
| Đáp án: | Áp dụng công thức \( \Delta x = \frac{\lambda D}{a} = \frac{600 \times 10^{-9} \times 2}{0,5 \times 10^{-3}} = 2,4 \, \text{mm} \). |

.png)
1. Lý thuyết Sóng ánh sáng
Sóng ánh sáng là một hiện tượng vật lý quan trọng, được phân tích dựa trên tính chất sóng và hạt của ánh sáng. Dưới đây là các khái niệm cơ bản và lý thuyết liên quan đến sóng ánh sáng:
- Bước sóng (\(\lambda\)): Là khoảng cách giữa hai đỉnh sóng liên tiếp. Đơn vị đo là mét (m).
- Tần số (f): Là số dao động của sóng trong một giây, đo bằng đơn vị Hertz (Hz). Công thức liên hệ giữa tần số và bước sóng là \(c = \lambda \cdot f\), trong đó \(c\) là vận tốc ánh sáng.
- Quang phổ: Ánh sáng có thể được phân tích thành nhiều màu khác nhau, gọi là quang phổ. Quang phổ liên tục, quang phổ vạch phát xạ và quang phổ hấp thụ là các loại phổ phổ biến.
- Giao thoa ánh sáng: Khi hai sóng ánh sáng gặp nhau, chúng có thể tăng cường hoặc triệt tiêu lẫn nhau. Đây là cơ sở của hiện tượng giao thoa.
- Nhiễu xạ: Hiện tượng ánh sáng bị uốn cong khi đi qua các khe hẹp hoặc chướng ngại vật, dẫn đến tạo ra các vân sáng tối.
- Hiệu ứng Doppler: Là sự thay đổi tần số và bước sóng của ánh sáng khi nguồn phát hoặc người quan sát chuyển động.
Các khái niệm trên là nền tảng để hiểu và giải quyết các bài toán liên quan đến sóng ánh sáng trong vật lý.
2. Phương pháp giải bài tập Sóng ánh sáng
Để giải quyết bài tập liên quan đến sóng ánh sáng, chúng ta cần hiểu rõ các khái niệm lý thuyết cơ bản và áp dụng chúng vào các bài tập cụ thể. Dưới đây là các bước tiếp cận và phương pháp chi tiết:
- Xác định các đại lượng liên quan:
- Độ dài sóng \(\lambda\)
- Tần số \(f\)
- Chu kỳ \(T = \frac{1}{f}\)
- Vận tốc sóng \(v = \lambda \cdot f\)
- Áp dụng công thức giao thoa ánh sáng:
Đối với hiện tượng giao thoa, sử dụng công thức:
\[ i = \frac{\lambda \cdot D}{a} \]trong đó:
- \(i\) là khoảng vân
- \(\lambda\) là bước sóng của ánh sáng
- \(D\) là khoảng cách từ màn chắn đến hai khe
- \(a\) là khoảng cách giữa hai khe
- Phân tích điều kiện giao thoa:
Xác định các vị trí của vân sáng và vân tối trên màn bằng cách sử dụng:
\[ \Delta d = k \lambda \]với \(k\) là bậc của vân sáng, và:
\[ \Delta d = (k + \frac{1}{2}) \lambda \]với \(k\) là bậc của vân tối.
- Giải bài tập tán sắc ánh sáng:
Áp dụng các công thức liên quan đến hiện tượng tán sắc để tìm các giá trị cần thiết, ví dụ:
\[ n = \frac{c}{v} \]với \(n\) là chiết suất, \(c\) là tốc độ ánh sáng trong chân không, và \(v\) là tốc độ ánh sáng trong môi trường.
- Kiểm tra kết quả:
Sau khi tính toán, so sánh kết quả với các đơn vị và điều kiện thực tế để đảm bảo tính hợp lý.

3. Bài tập Sóng ánh sáng
Dưới đây là một số bài tập thực hành về sóng ánh sáng giúp củng cố kiến thức và kỹ năng giải quyết các vấn đề liên quan:
- Bài tập 1: Tính khoảng vân giao thoa
Hai nguồn sáng đơn sắc có bước sóng \(\lambda = 600 nm\) phát ra từ hai khe cách nhau \(a = 1 mm\). Màn ảnh đặt cách hai khe một khoảng \(D = 2 m\). Tính khoảng vân giao thoa \(i\).
Giải:
\[ i = \frac{\lambda \cdot D}{a} = \frac{600 \times 10^{-9} \times 2}{1 \times 10^{-3}} = 1.2 \times 10^{-3} m = 1.2 mm \] - Bài tập 2: Tìm vị trí vân sáng bậc 3
Với các thông số từ bài tập 1, hãy tìm vị trí vân sáng bậc 3 trên màn ảnh.
Giải:
\[ x = k \cdot i = 3 \times 1.2 = 3.6 mm \]Vậy vị trí vân sáng bậc 3 cách vị trí trung tâm \(3.6 mm\).
- Bài tập 3: Tính chiết suất của môi trường
Một chùm sáng có bước sóng \(\lambda = 500 nm\) khi đi từ không khí vào môi trường có chiết suất \(n\) thì bước sóng của nó giảm xuống còn \(\lambda' = 400 nm\). Tính chiết suất \(n\) của môi trường đó.
Giải:
\[ n = \frac{\lambda}{\lambda'} = \frac{500}{400} = 1.25 \] - Bài tập 4: Tính vận tốc ánh sáng trong một môi trường
Ánh sáng có vận tốc \(c = 3 \times 10^8 m/s\) trong chân không. Khi đi vào một môi trường, vận tốc của nó giảm còn \(v = 2.5 \times 10^8 m/s\). Tính chiết suất \(n\) của môi trường đó.
Giải:
\[ n = \frac{c}{v} = \frac{3 \times 10^8}{2.5 \times 10^8} = 1.2 \]