Chủ đề lục giác đều: Lục giác đều là một trong những hình học cơ bản với nhiều đặc điểm thú vị. Bài viết này sẽ giới thiệu chi tiết về định nghĩa, công thức tính toán và các ứng dụng thực tiễn của lục giác đều trong đời sống và khoa học.
Mục lục
- Lục Giác Đều
- 1. Định Nghĩa và Đặc Điểm Của Lục Giác Đều
- 2. Công Thức Tính Toán Liên Quan Đến Lục Giác Đều
- 3. Phương Pháp Vẽ Lục Giác Đều
- 4. Ứng Dụng Thực Tiễn Của Lục Giác Đều
- YOUTUBE: Video hướng dẫn cách vẽ lục giác đều trong 5 giây bằng phần mềm GSP cực kì đơn giản, phù hợp cho học sinh lớp 6 theo sách giáo khoa mới.
Lục Giác Đều
Lục giác đều là một hình đa giác có sáu cạnh và sáu góc bằng nhau, được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau từ kiến trúc đến công nghệ.
Đặc điểm của Lục Giác Đều
- Mỗi cạnh có độ dài bằng nhau.
- Mỗi góc trong của lục giác đều là \(120^\circ\).
- Tổng số đo các góc trong của lục giác đều là \(720^\circ\).
- Tâm của đường tròn ngoại tiếp lục giác đều cũng là tâm đối xứng quay.
Công thức tính các đại lượng trong Lục Giác Đều
Trong toán học, công thức tính tổng góc trong của một đa giác là \( (n-2) \times 180^\circ \), với \( n \) là số cạnh. Đối với lục giác đều, áp dụng công thức này cho \( n = 6 \), ta có tổng góc trong là \( 720^\circ \).
Công thức tính góc trong của một lục giác đều:
\[
\text{Góc nội} = \frac{(n-2) \times 180^\circ}{n} = \frac{(6-2) \times 180^\circ}{6} = 120^\circ
\]
Bảng Tóm Tắt
| Tổng số góc trong | 720 độ |
| Góc mỗi đỉnh | 120 độ |
| Tính đối xứng | Tâm đường tròn ngoại tiếp là tâm đối xứng quay |
Các ứng dụng thực tế của Lục Giác Đều
Lục giác đều có rất nhiều ứng dụng trong thực tế nhờ vào tính đối xứng và cân bằng của nó:
- Kiến trúc và xây dựng: Lục giác đều được sử dụng trong thiết kế gạch lát ốp tường, mái đền, và các công trình kiến trúc khác.
- Công nghệ: Trong lĩnh vực công nghệ, lục giác đều giúp mô hình hoá cấu trúc phân tử của các vật liệu như kim cương và graphite.
- Nghệ thuật và thiết kế: Lục giác đều là hình dạng cơ bản trong thiết kế hoa văn, tranh ảnh và sản xuất đồ dùng như khay đựng kẹo và đèn thả.
Phương pháp vẽ Lục Giác Đều
Có nhiều cách để vẽ lục giác đều, dưới đây là một số phương pháp phổ biến:
- Sử dụng compa và thước kẻ: Vẽ một đường tròn, chọn một điểm trên đường tròn làm điểm bắt đầu và dùng compa để chia đường tròn thành sáu đoạn bằng nhau, sau đó nối các điểm này lại với nhau.
- Sử dụng thước và ê ke: Vẽ một cạnh của lục giác, sau đó dùng ê ke để vẽ các cạnh còn lại với góc \(120^\circ\) giữa mỗi cạnh.
Với những kiến thức cơ bản và ứng dụng của lục giác đều, hy vọng bạn sẽ có cái nhìn toàn diện về hình học này và áp dụng được vào thực tế.

.png)
1. Định Nghĩa và Đặc Điểm Của Lục Giác Đều
Lục giác đều là một đa giác có sáu cạnh và sáu góc bằng nhau. Đây là một trong những hình học cơ bản và phổ biến nhất trong toán học và ứng dụng thực tiễn.
1.1. Định Nghĩa
Một lục giác đều có các cạnh và các góc bằng nhau, mỗi góc trong của lục giác đều bằng \(120^\circ\). Các cạnh của lục giác đều bằng nhau và tạo thành các góc đều nhau tại mỗi đỉnh.
1.2. Đặc Điểm Hình Học
- Các cạnh bằng nhau.
- Các góc bằng nhau, mỗi góc bằng \(120^\circ\).
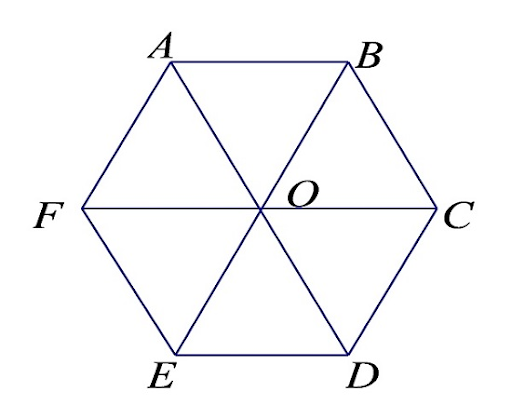
- Nó có thể được chia thành sáu tam giác đều nhỏ hơn.
1.3. Công Thức Tính Chu Vi
Chu vi của lục giác đều được tính bằng tổng chiều dài của sáu cạnh:
\[ P = 6a \]
Trong đó, \( a \) là độ dài của một cạnh.
1.4. Công Thức Tính Diện Tích
Diện tích của lục giác đều có thể được tính bằng công thức:
\[ A = \frac{3\sqrt{3}}{2}a^2 \]
Trong đó, \( a \) là độ dài của một cạnh.
1.5. Đặc Điểm Đối Xứng
- Lục giác đều có đối xứng quay quanh tâm một góc \(60^\circ\).
- Có sáu trục đối xứng đi qua các đỉnh và trung điểm các cạnh đối diện.
1.6. Các Dạng Biến Thể
- Lục giác nội tiếp trong đường tròn: Tất cả các đỉnh đều nằm trên một đường tròn.
- Lục giác ngoại tiếp đường tròn: Tất cả các cạnh đều tiếp xúc với một đường tròn bên trong.
2. Công Thức Tính Toán Liên Quan Đến Lục Giác Đều
Các công thức tính toán liên quan đến lục giác đều giúp chúng ta hiểu rõ hơn về các đặc điểm hình học của nó và áp dụng trong các bài toán thực tiễn.
2.1. Công Thức Tính Chu Vi
Chu vi của lục giác đều được tính bằng tổng chiều dài của sáu cạnh:
\[ P = 6a \]
Trong đó, \( a \) là độ dài của một cạnh.
2.2. Công Thức Tính Diện Tích
Diện tích của lục giác đều có thể được tính bằng công thức:
\[ A = \frac{3\sqrt{3}}{2}a^2 \]
Trong đó, \( a \) là độ dài của một cạnh.
2.3. Công Thức Tính Bán Kính Đường Tròn Nội Tiếp
Bán kính của đường tròn nội tiếp lục giác đều:
\[ r = \frac{\sqrt{3}}{2}a \]
2.4. Công Thức Tính Bán Kính Đường Tròn Ngoại Tiếp
Bán kính của đường tròn ngoại tiếp lục giác đều:
\[ R = a \]
2.5. Các Công Thức Liên Quan Khác
- Chiều cao của lục giác đều:
\[ h = \sqrt{3}a \] - Góc tại các đỉnh của lục giác đều:
\[ 120^\circ \] - Đường chéo chính của lục giác đều (nối hai đỉnh đối diện):
\[ d = 2a \]

3. Phương Pháp Vẽ Lục Giác Đều
Vẽ lục giác đều là một kỹ năng hữu ích trong hình học. Dưới đây là các bước cơ bản để vẽ một hình lục giác đều một cách chính xác.
- Chuẩn bị dụng cụ: Bạn cần có compa, thước kẻ, bút chì và tẩy để đảm bảo độ chính xác.
Các bước vẽ lục giác đều:
- Vẽ đường tròn ngoại tiếp: Sử dụng compa để vẽ một đường tròn với bán kính \( R \).
- Xác định các điểm đỉnh: Đặt mũi nhọn của compa tại một điểm trên đường tròn (gọi là điểm \( A \)). Mở rộng compa sao cho khoảng cách bằng bán kính \( R \) của đường tròn và vẽ cung tròn cắt đường tròn tại điểm mới (gọi là \( B \)). Lặp lại quá trình này từ điểm \( B \) để xác định các điểm \( C, D, E, F \), đảm bảo mỗi cung tròn cắt đường tròn tại các điểm mới.
- Nối các điểm: Sử dụng thước kẻ để nối các điểm \( A, B, C, D, E, F \) để tạo thành hình lục giác đều. Mỗi cạnh của lục giác đều sẽ có độ dài bằng bán kính \( R \) của đường tròn ngoại tiếp.
- Kiểm tra độ chính xác: Đảm bảo rằng tất cả các cạnh của lục giác đều bằng nhau và các góc giữa các cạnh đều bằng \( 120^\circ \).
- Hoàn thiện: Dùng tẩy để xóa các đường tròn và dấu nháp không cần thiết, chỉ để lại hình lục giác đều hoàn chỉnh.
Dưới đây là một số lưu ý khi vẽ lục giác đều:
- Đảm bảo rằng compa và thước kẻ được sử dụng đúng cách để đạt độ chính xác cao nhất.
- Kiểm tra lại các kích thước và góc để chắc chắn rằng hình vẽ là lục giác đều hoàn chỉnh.
XEM THÊM:
4. Ứng Dụng Thực Tiễn Của Lục Giác Đều
Lục giác đều không chỉ là một hình học thuần túy mà còn có nhiều ứng dụng trong thực tiễn, từ tự nhiên đến kiến trúc và kỹ thuật:
- Tổ ong: Tổ ong là một ví dụ nổi tiếng về việc sử dụng lục giác đều trong tự nhiên. Ong tạo ra các ô tổ với hình lục giác đều giúp tối ưu hóa không gian và vật liệu xây dựng.
- Kiến trúc và thiết kế: Lục giác đều được sử dụng trong thiết kế lát sàn, tạo mẫu gạch ốp tường, và cả trong kiến trúc để tạo ra các cấu trúc vừa vững chãi vừa thẩm mỹ.
- Khoa học vật liệu: Các cấu trúc lục giác đều được tìm thấy trong các tinh thể và vật liệu, chẳng hạn như graphene, một dạng của carbon có cấu trúc lục giác đều, nổi tiếng với độ bền và khả năng dẫn điện tuyệt vời.
- Toán học và trò chơi: Lục giác đều cũng xuất hiện trong các bài toán toán học và trò chơi trí tuệ, chẳng hạn như bàn cờ Hex, nơi người chơi cạnh tranh để tạo ra một chuỗi liên kết từ một cạnh của bàn cờ sang cạnh đối diện.
Như vậy, từ tự nhiên đến nhân tạo, lục giác đều xuất hiện khắp nơi trong cuộc sống hàng ngày và tiếp tục làm nguồn cảm hứng cho nhiều lĩnh vực nghiên cứu và phát triển.























