Chủ đề đường tròn lượng giác: Đường tròn lượng giác là công cụ quan trọng trong toán học, giúp hiểu rõ và áp dụng các hàm số lượng giác. Bài viết này sẽ giới thiệu từ khái niệm cơ bản đến các ứng dụng thực tiễn, cùng với các bài tập chi tiết để giúp bạn nắm vững kiến thức này một cách hiệu quả.
Mục lục
- Đường Tròn Lượng Giác
- 1. Khái niệm Đường Tròn Lượng Giác
- 2. Các điểm và trục trên Đường Tròn Lượng Giác
- 3. Hàm số Lượng Giác trên Đường Tròn Đơn Vị
- 4. Ứng dụng của Đường Tròn Lượng Giác
- 5. Các dạng bài tập về Đường Tròn Lượng Giác
- 6. Lưu ý khi học và sử dụng Đường Tròn Lượng Giác
- YOUTUBE: Khám phá cách sử dụng đường tròn lượng giác một cách hiệu quả và dễ hiểu với video hướng dẫn chi tiết. Nắm vững các khái niệm và ứng dụng thực tế trong toán học.
Đường Tròn Lượng Giác
Đường tròn lượng giác là một khái niệm quan trọng trong toán học, đặc biệt là trong lượng giác. Đây là một đường tròn trên mặt phẳng tọa độ Oxy với tâm O và bán kính R = 1. Đường tròn lượng giác giúp biểu diễn các giá trị lượng giác của các góc đặc biệt.
Các giá trị lượng giác cơ bản
Dưới đây là bảng liệt kê các giá trị lượng giác cơ bản của một số góc phổ biến:
| Góc | Sin | Cos | Tan |
|---|---|---|---|
| 0° (\(0\)) | 0 | 1 | 0 |
| 30° (\(\frac{\pi}{6}\)) | \(\frac{1}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{\sqrt{3}}\) |
| 45° (\(\frac{\pi}{4}\)) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{2}}{2}\) | 1 |
| 60° (\(\frac{\pi}{3}\)) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{2}\) | \(\sqrt{3}\) |
| 90° (\(\frac{\pi}{2}\)) | 1 | 0 | Không xác định |
Biểu diễn góc trên đường tròn lượng giác
Để biểu diễn góc lượng giác có số đo α trên đường tròn lượng giác, ta thực hiện các bước sau:
- Vẽ đường tròn lượng giác, chọn gốc A(1; 0) làm điểm đầu.
- Chọn điểm cuối M trên đường tròn sao cho \( (OA, OM) = α \).
- Điểm cuối M chính là điểm biểu diễn của góc α.
Nếu \( |α| > 2π \) (hoặc \( |α| > 360° \)), ta phân tích \( α = β + k2π \) (hoặc \( α = β + k360° \)) với \( – π < β < π \). Khi đó, β là góc biểu diễn trên đường tròn.
Góc và Cung Đặc Biệt
Vòng tròn lượng giác chứa nhiều góc và cung đặc biệt gọi là "góc chuẩn", có giá trị lượng giác đặc biệt giúp đơn giản hóa việc giải toán:
- Góc 0° (0 radian): Điểm bắt đầu, sin = 0 và cos = 1.
- Góc 90° (\(\frac{\pi}{2}\) radian): Điểm ở đỉnh, sin = 1 và cos = 0.
- Góc 180° (\(\pi\) radian): Điểm đối diện với điểm bắt đầu, sin = 0 và cos = -1.
- Góc 270° (\(\frac{3\pi}{2}\) radian): Điểm ở cạnh dưới, sin = -1 và cos = 0.
- Góc 360° (2\(\pi\) radian): Hoàn thành một vòng tròn, trở lại điểm bắt đầu.
Hi vọng những kiến thức trên sẽ giúp bạn hiểu rõ hơn về đường tròn lượng giác và ứng dụng của nó trong học tập và giải toán.

.png)
1. Khái niệm Đường Tròn Lượng Giác
Đường tròn lượng giác là một công cụ quan trọng trong toán học, đặc biệt trong việc hiểu và biểu diễn các hàm số lượng giác. Đường tròn này nằm trên mặt phẳng tọa độ Oxy với tâm tại gốc tọa độ (0,0) và bán kính bằng 1, do đó còn được gọi là đường tròn đơn vị.
Một số khái niệm cơ bản liên quan đến đường tròn lượng giác bao gồm:
- Tâm đường tròn: Điểm O (0, 0).
- Bán kính: R = 1.
- Chu vi: \(2\pi\).
Trong đường tròn lượng giác, mỗi điểm trên đường tròn có thể được biểu diễn bằng một góc \(\theta\) tính từ trục hoành dương theo chiều kim đồng hồ. Góc này thường được đo bằng rađian.
1.1. Các điểm quan trọng trên đường tròn lượng giác
- Góc 0°: Điểm (1, 0).
- Góc 90°: Điểm (0, 1).
- Góc 180°: Điểm (-1, 0).
- Góc 270°: Điểm (0, -1).
1.2. Công thức lượng giác trên đường tròn
Các hàm số lượng giác có thể được biểu diễn trên đường tròn lượng giác như sau:
| Sin(\(\theta\)): | Độ dài đoạn vuông góc từ điểm đó đến trục hoành, tương ứng với tọa độ y của điểm trên đường tròn. |
| Cos(\(\theta\)): | Độ dài đoạn thẳng từ gốc tọa độ đến điểm chiếu của điểm đó trên trục hoành, tương ứng với tọa độ x của điểm trên đường tròn. |
| Tan(\(\theta\)): | Được tính bằng tỷ số \(\frac{Sin(\theta)}{Cos(\theta)}\), tức là \(y/x\). |
Công thức lượng giác cơ bản:
\[
\sin(\theta) = \frac{\text{Đối}}{\text{Huyền}}
\]
\[
\cos(\theta) = \frac{\text{Kề}}{\text{Huyền}}
\]
\]
\]
\[
\tan(\theta) = \frac{\text{Đối}}{\text{Kề}}
\]
1.3. Vai trò trong toán học
Đường tròn lượng giác giúp chúng ta dễ dàng hình dung và tính toán các giá trị lượng giác. Nó cũng là nền tảng để giải các phương trình lượng giác phức tạp và áp dụng trong nhiều lĩnh vực khác như vật lý và kỹ thuật.
2. Các điểm và trục trên Đường Tròn Lượng Giác
Đường tròn lượng giác là công cụ mạnh mẽ giúp biểu diễn và tính toán các giá trị lượng giác. Để hiểu rõ hơn, chúng ta sẽ xem xét các điểm và trục trên đường tròn này.
2.1. Điểm ngọn của các cung đặc biệt
Trên đường tròn lượng giác, các điểm ngọn của các cung đặc biệt bao gồm:
- Điểm \(A (1, 0)\) tương ứng với góc 0° hoặc 360°.
- Điểm \(B (0, 1)\) tương ứng với góc 90°.
- Điểm \(A' (-1, 0)\) tương ứng với góc 180°.
- Điểm \(B' (0, -1)\) tương ứng với góc 270°.
2.2. Trục Sin và Cos
Đường tròn lượng giác được chia bởi hai trục chính:
- Trục Sin: Trục này là đường thẳng ngang qua tâm \(O\), chia đường tròn thành hai phần bằng nhau. Trục sin giúp xác định giá trị sin của các góc.
- Trục Cos: Trục này là đường thẳng dọc qua tâm \(O\), chia đường tròn thành hai phần bằng nhau. Trục cos giúp xác định giá trị cos của các góc.
2.3. Trục Tan và Cotan
Để xác định các giá trị tan và cotan, ta sử dụng các trục:
- Trục Tan: Được xác định bằng cách kẻ đường thẳng tiếp tuyến với đường tròn tại điểm \(A (1, 0)\). Giá trị tan của góc \(\alpha\) bằng độ dài đoạn thẳng từ điểm giao của trục tan với đường thẳng song song trục sin tại góc \(\alpha\).
- Trục Cotan: Được xác định bằng cách kẻ đường thẳng tiếp tuyến với đường tròn tại điểm \(B (0, 1)\). Giá trị cotan của góc \(\alpha\) bằng độ dài đoạn thẳng từ điểm giao của trục cotan với đường thẳng song song trục cos tại góc \(\alpha\).
| Góc | Điểm ngọn | Sin | Cos |
|---|---|---|---|
| 0° (hoặc \(2\pi k\), \(k\in\mathbb{Z}\)) | A (1,0) | 0 | 1 |
| 90° (hoặc \(\dfrac{\pi}{2} + 2\pi k\)) | B (0,1) | 1 | 0 |
| 180° (hoặc \(\pi + 2\pi k\)) | A' (-1,0) | 0 | -1 |
| 270° (hoặc \(\dfrac{3\pi}{2} + 2\pi k\)) | B' (0,-1) | -1 | 0 |

3. Hàm số Lượng Giác trên Đường Tròn Đơn Vị
Đường tròn đơn vị là một công cụ quan trọng trong việc hiểu các hàm số lượng giác. Đường tròn này có bán kính bằng 1 và tâm tại gốc tọa độ (0, 0).
Các hàm số lượng giác bao gồm:
- Hàm Sine (sin): Được định nghĩa là tỷ số giữa cạnh đối và cạnh huyền trong tam giác vuông, trên đường tròn đơn vị, đây là tọa độ y của điểm P.
- Hàm Cosine (cos): Được định nghĩa là tỷ số giữa cạnh kề và cạnh huyền, trên đường tròn đơn vị, đây là tọa độ x của điểm P.
- Hàm Tangent (tan): Được định nghĩa là tỷ số giữa cạnh đối và cạnh kề, trên đường tròn đơn vị, tan = sin/cos.
| Góc | Sin | Cos | Tan |
|---|---|---|---|
| 0° (0 rad) | 0 | 1 | 0 |
| 30° (π/6 rad) | \(\frac{1}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{\sqrt{3}}\) |
| 45° (π/4 rad) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{2}}{2}\) | 1 |
| 60° (π/3 rad) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{2}\) | \(\sqrt{3}\) |
| 90° (π/2 rad) | 1 | 0 | Không xác định |
Các công thức lượng giác cơ bản trên đường tròn đơn vị:
- \( \sin^2 \theta + \cos^2 \theta = 1 \)
- \( \tan \theta = \frac{\sin \theta}{\cos \theta} \)
- \( \cot \theta = \frac{1}{\tan \theta} \)
Trên đường tròn đơn vị, các góc đặc biệt và các giá trị lượng giác của chúng rất quan trọng trong việc giải các phương trình và bài toán lượng giác.
4. Ứng dụng của Đường Tròn Lượng Giác
Đường tròn lượng giác là một công cụ toán học mạnh mẽ với nhiều ứng dụng trong các lĩnh vực khác nhau. Dưới đây là một số ứng dụng tiêu biểu:
- Giải phương trình lượng giác:
Đường tròn lượng giác giúp đơn giản hóa việc giải các phương trình lượng giác phức tạp bằng cách sử dụng các giá trị lượng giác cơ bản và mối quan hệ giữa chúng.
- Ứng dụng trong hình học:
Đường tròn lượng giác được sử dụng để tính toán các góc và khoảng cách trong không gian ba chiều, hỗ trợ trong việc giải các bài toán hình học phẳng và không gian.
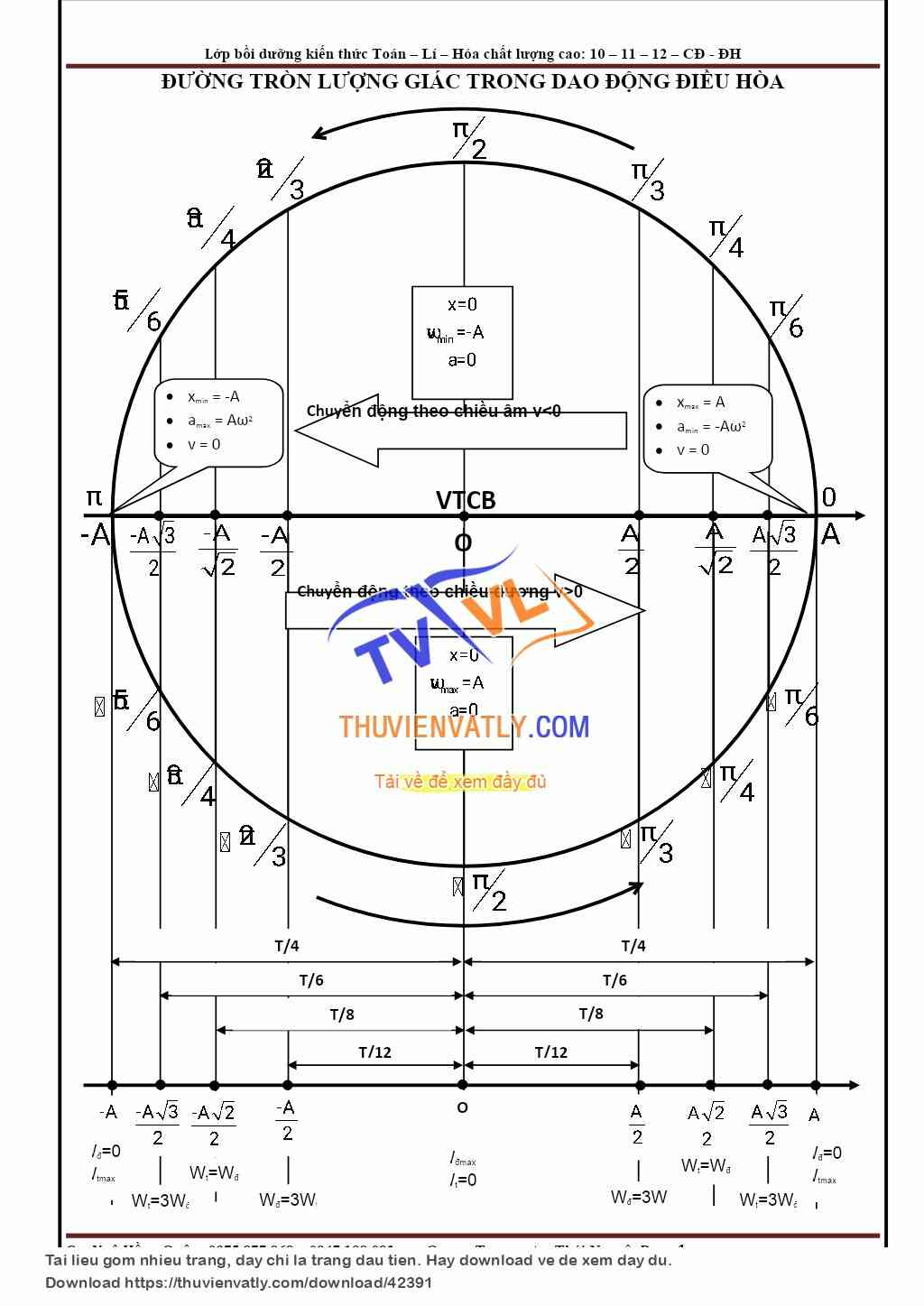
- Ứng dụng trong vật lý:
Trong vật lý, đường tròn lượng giác được sử dụng để mô tả dao động điều hòa, sóng, và các hiện tượng tuần hoàn khác. Ví dụ, phương trình dao động điều hòa có thể được biểu diễn dưới dạng hàm lượng giác:
\(x(t) = A \cos(\omega t + \varphi)\)Trong đó:
- \(A\) là biên độ dao động
- \(\omega\) là tần số góc
- \(\varphi\) là pha ban đầu
- Ứng dụng trong kỹ thuật:
Đường tròn lượng giác được sử dụng trong thiết kế hệ thống điều khiển, cảm biến, và các mạch điện tử. Việc hiểu các giá trị lượng giác giúp cải thiện hiệu suất và độ chính xác của các hệ thống này.
- Ứng dụng trong đồ họa và trò chơi:
Trong thiết kế đồ họa và phát triển trò chơi, đường tròn lượng giác được sử dụng để tính toán các hiệu ứng đặc biệt, vị trí và hướng di chuyển của các đối tượng.

5. Các dạng bài tập về Đường Tròn Lượng Giác
Đường tròn lượng giác là công cụ quan trọng trong toán học, giúp giải quyết nhiều bài toán từ cơ bản đến phức tạp. Dưới đây là một số dạng bài tập phổ biến liên quan đến đường tròn lượng giác:
- Đổi độ sang rađian và ngược lại:
- Ví dụ: Chuyển đổi 45° sang radian.
\[
45^\circ = \frac{45 \pi}{180} = \frac{\pi}{4}
\] - Ví dụ: Chuyển đổi \(\frac{\pi}{3}\) radian sang độ.
\[
\frac{\pi}{3} \text{ rad} = \frac{\pi}{3} \times \frac{180}{\pi} = 60^\circ
\]
- Ví dụ: Chuyển đổi 45° sang radian.
- Biểu diễn cung lượng giác:
- Ví dụ: Tính giá trị của \(\sin\) và \(\cos\) của các góc đặc biệt như 30°, 45°, và 60°.
- \(\sin 30^\circ = \frac{1}{2}\)
- \(\cos 45^\circ = \frac{\sqrt{2}}{2}\)
- \(\tan 60^\circ = \sqrt{3}\)
- Ví dụ: Tính giá trị của \(\sin\) và \(\cos\) của các góc đặc biệt như 30°, 45°, và 60°.
- Xác định vị trí điểm trên đường tròn:
- Ví dụ: Xác định tọa độ của điểm tại góc 120°.
\[
\cos 120^\circ = -\frac{1}{2}, \sin 120^\circ = \frac{\sqrt{3}}{2}
\]
- Ví dụ: Xác định tọa độ của điểm tại góc 120°.
- Ứng dụng trong giải phương trình lượng giác:
- Ví dụ: Giải phương trình \(\sin x = \frac{1}{2}\) trong khoảng từ 0 đến 2π.
\[
x = \frac{\pi}{6} \text{ hoặc } x = \frac{5\pi}{6}
\]
- Ví dụ: Giải phương trình \(\sin x = \frac{1}{2}\) trong khoảng từ 0 đến 2π.
Các bài tập trên giúp học sinh nắm vững cách sử dụng đường tròn lượng giác, từ đó áp dụng vào các bài toán thực tế và học thuật một cách hiệu quả.
XEM THÊM:
6. Lưu ý khi học và sử dụng Đường Tròn Lượng Giác
Khi học và sử dụng đường tròn lượng giác, có một số lưu ý quan trọng cần ghi nhớ để nắm bắt kiến thức hiệu quả hơn:
- Biểu diễn góc chính xác: Đảm bảo rằng bạn sử dụng đúng đơn vị đo góc (độ hoặc radian) khi biểu diễn góc trên đường tròn lượng giác.
- Hiểu rõ các giá trị đặc biệt: Các giá trị đặc biệt của sin, cos, tan tại các góc 0°, 30°, 45°, 60°, 90°, 180° và 270° cần được ghi nhớ và hiểu rõ.
- Thực hành đều đặn: Giải nhiều bài tập để quen thuộc với việc biểu diễn và tính toán trên đường tròn lượng giác.
6.1. Các lỗi thường gặp
Trong quá trình học đường tròn lượng giác, học sinh thường gặp một số lỗi phổ biến:
- Lỗi đơn vị đo: Sử dụng sai đơn vị đo (độ thay vì radian và ngược lại) có thể dẫn đến kết quả sai.
- Nhầm lẫn giữa sin và cos: Đôi khi học sinh nhầm lẫn giữa trục sin và trục cos, dẫn đến việc tính toán sai giá trị.
- Quên giá trị âm dương: Không nhớ rằng giá trị của các hàm lượng giác có thể âm hoặc dương tùy thuộc vào góc và vị trí trên đường tròn lượng giác.
6.2. Mẹo ghi nhớ và học nhanh
Để học nhanh và hiệu quả, hãy tham khảo các mẹo sau:
- Sử dụng bảng giá trị: Bảng giá trị của các hàm lượng giác tại các góc đặc biệt có thể giúp bạn dễ dàng tra cứu và ghi nhớ.
- Vẽ sơ đồ: Vẽ đường tròn lượng giác và đánh dấu các góc đặc biệt thường xuyên sẽ giúp bạn hình dung rõ hơn về mối quan hệ giữa các giá trị lượng giác.
- Thực hành với công cụ trực tuyến: Sử dụng các công cụ trực tuyến và ứng dụng học toán để thực hành biểu diễn và tính toán trên đường tròn lượng giác.
Áp dụng các lưu ý và mẹo trên sẽ giúp bạn học và sử dụng đường tròn lượng giác một cách hiệu quả và chính xác.






















