Entropy và Biến Thiên Năng Lượng Tự Do Gibbs: Hiểu Rõ và Ứng Dụng Thực Tiễn

Trong lĩnh vực nhiệt động lực học, hai khái niệm quan trọng thường được nhắc đến là entropy và biến thiên năng lượng tự do Gibbs. Đây là những yếu tố then chốt giúp dự đoán sự tự phát của quá trình hóa học và vật lý.

1. Entropy (S)

Entropy là một đại lượng thể hiện mức độ hỗn loạn hay rối loạn của hệ thống. Khi một quá trình xảy ra, sự rối loạn của hệ thống thường tăng lên, dẫn đến sự gia tăng entropy. Định luật thứ hai của nhiệt động lực học nêu rằng entropy của vũ trụ luôn tăng lên trong một quá trình tự phát. Điều này có nghĩa là các quá trình tự nhiên có xu hướng chuyển từ trật tự sang hỗn loạn.

Công thức tính entropy trong một quá trình nhiệt động lực học đơn giản có thể được biểu diễn bằng:

\[ \Delta S = \frac{Q_{rev}}{T} \]

Trong đó:

• \( \Delta S \): Sự thay đổi entropy
• \( Q_{rev} \): Nhiệt lượng trao đổi trong quá trình thuận nghịch
• \( T \): Nhiệt độ tuyệt đối của hệ

2. Năng Lượng Tự Do Gibbs (G)

Năng lượng tự do Gibbs là một hàm nhiệt động lực học, dùng để dự đoán tính tự phát của một phản ứng hóa học. Biến thiên năng lượng tự do Gibbs giúp xác định liệu một phản ứng có thể xảy ra tự phát ở điều kiện nhiệt độ và áp suất không đổi hay không.

Công thức tính biến thiên năng lượng tự do Gibbs:

\[ \Delta G = \Delta H - T\Delta S \]

Trong đó:

• \( \Delta G \): Biến thiên năng lượng tự do Gibbs
• \( \Delta H \): Biến thiên enthalpy (nhiệt chứa)
• \( \Delta S \): Biến thiên entropy

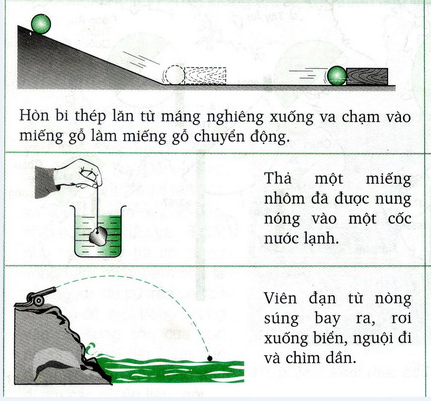
Nếu \( \Delta G < 0 \), phản ứng xảy ra tự phát. Nếu \( \Delta G > 0 \), phản ứng không tự phát. Trường hợp \( \Delta G = 0 \) thể hiện hệ đang ở trạng thái cân bằng.

3. Ứng Dụng Thực Tế

Hiểu rõ mối quan hệ giữa entropy và năng lượng tự do Gibbs là rất quan trọng trong các ngành công nghiệp như hóa chất, năng lượng, và công nghệ vật liệu. Việc tính toán đúng \( \Delta G \) giúp tối ưu hóa quy trình sản xuất, tiết kiệm năng lượng và giảm thiểu tác động môi trường.

4. Tổng Kết

Entropy và biến thiên năng lượng tự do Gibbs không chỉ là các khái niệm lý thuyết mà còn có giá trị ứng dụng thực tiễn lớn trong đời sống và sản xuất. Sự hiểu biết sâu về hai khái niệm này giúp chúng ta có thể dự đoán và kiểm soát các quá trình hóa học và vật lý, từ đó đóng góp vào sự phát triển bền vững và tiến bộ khoa học kỹ thuật.

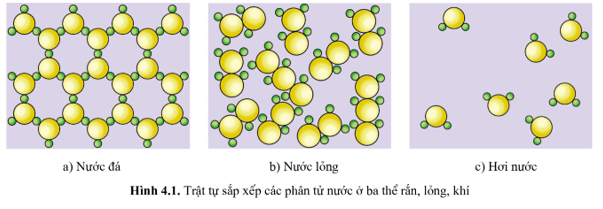
Entropy là một khái niệm quan trọng trong nhiệt động lực học, dùng để đo lường mức độ hỗn loạn hoặc rối loạn trong một hệ thống. Thuật ngữ này được xuất phát từ tiếng Hy Lạp, với nghĩa là "sự biến đổi". Trong các quá trình tự nhiên, entropy thường có xu hướng tăng, điều này biểu thị sự chuyển đổi từ trạng thái có trật tự sang trạng thái hỗn loạn hơn.

Entropy được định nghĩa trong bối cảnh nhiệt động lực học như sau:

\[ S = k_B \ln \Omega \]

Trong đó:

• \( S \): Entropy
• \( k_B \): Hằng số Boltzmann
• \( \Omega \): Số lượng trạng thái vi mô có thể xảy ra tương ứng với một trạng thái vĩ mô cụ thể

Entropy không chỉ là một đại lượng lý thuyết mà còn có ý nghĩa thực tiễn quan trọng trong nhiều ngành khoa học, bao gồm vật lý, hóa học, và kỹ thuật. Hiểu rõ về entropy giúp chúng ta dự đoán và kiểm soát các quá trình tự nhiên, từ đó tối ưu hóa các hệ thống trong nghiên cứu và công nghiệp.

Biến thiên năng lượng tự do Gibbs (\( \Delta G \)) là một khái niệm quan trọng trong nhiệt động lực học, dùng để dự đoán tính tự phát của các phản ứng hóa học và quá trình vật lý. Năng lượng tự do Gibbs kết hợp hai yếu tố chính: enthalpy (nhiệt hàm) và entropy của hệ thống, từ đó xác định xem một quá trình có thể diễn ra tự phát hay không.

Biến thiên năng lượng tự do Gibbs được tính bằng công thức:

\[ \Delta G = \Delta H - T \Delta S \]

Trong đó:

• \( \Delta G \): Biến thiên năng lượng tự do Gibbs
• \( \Delta H \): Biến thiên enthalpy (nhiệt hàm)
• \( T \): Nhiệt độ tuyệt đối (Kelvin)
• \( \Delta S \): Biến thiên entropy

Khi \( \Delta G < 0 \), phản ứng hoặc quá trình diễn ra tự phát. Ngược lại, nếu \( \Delta G > 0 \), phản ứng không tự phát và cần có sự can thiệp từ bên ngoài để xảy ra. Khi \( \Delta G = 0 \), hệ thống ở trạng thái cân bằng, và không có sự thay đổi nào trong hệ thống.

Biến thiên năng lượng tự do Gibbs không chỉ có giá trị trong lý thuyết mà còn được ứng dụng rộng rãi trong các lĩnh vực như hóa học, sinh học, và công nghệ. Nó cho phép các nhà khoa học dự đoán và điều chỉnh các phản ứng hóa học, từ việc phát triển dược phẩm cho đến thiết kế quy trình công nghiệp hiệu quả.

Entropy và năng lượng tự do Gibbs có mối liên hệ chặt chẽ trong việc xác định tính tự phát của các quá trình nhiệt động lực học. Trong công thức tính năng lượng tự do Gibbs:

\[ \Delta G = \Delta H - T \Delta S \]

Entropy (\( \Delta S \)) đóng vai trò quan trọng trong việc điều chỉnh giá trị của \( \Delta G \). Một sự thay đổi trong entropy của hệ thống sẽ ảnh hưởng trực tiếp đến sự tự phát của quá trình. Cụ thể:

• Nếu \( \Delta S > 0 \) và \( \Delta H < 0 \), quá trình sẽ luôn tự phát vì \( \Delta G < 0 \).
• Nếu \( \Delta S > 0 \) và \( \Delta H > 0 \), quá trình sẽ tự phát ở nhiệt độ cao khi \( T \Delta S \) lớn hơn \( \Delta H \).
• Nếu \( \Delta S < 0 \) và \( \Delta H < 0 \), quá trình sẽ tự phát ở nhiệt độ thấp khi \( T \Delta S \) nhỏ hơn \( \Delta H \).
• Nếu \( \Delta S < 0 \) và \( \Delta H > 0 \), quá trình không tự phát vì \( \Delta G > 0 \).

Như vậy, entropy không chỉ đơn thuần là một đại lượng đo lường sự hỗn loạn mà còn là yếu tố quyết định đến sự tự phát của các phản ứng và quá trình hóa học. Việc hiểu rõ mối quan hệ này giúp chúng ta dự đoán và kiểm soát các quá trình một cách chính xác hơn.

Entropy và năng lượng tự do Gibbs là những khái niệm quan trọng trong nhiệt động lực học, và có rất nhiều ứng dụng trong các ngành công nghiệp và khoa học hiện đại. Các ứng dụng này không chỉ giúp tối ưu hóa quá trình sản xuất, mà còn hỗ trợ phát triển các công nghệ tiên tiến và bảo vệ môi trường.

4.1 Ứng Dụng trong Công Nghệ Vật Liệu

Trong ngành công nghệ vật liệu, entropy và Gibbs Free Energy được sử dụng để dự đoán và kiểm soát các phản ứng hóa học trong quá trình tạo ra các vật liệu mới. Các quá trình như kết tinh, biến đổi pha, và tổng hợp vật liệu được quản lý dựa trên việc tính toán và điều chỉnh biến thiên năng lượng tự do Gibbs để đảm bảo tính ổn định và chất lượng của sản phẩm cuối cùng.

• Ứng dụng trong sản xuất hợp kim và vật liệu composite.
• Quản lý quá trình gia công vật liệu dựa trên sự thay đổi của entropy.
• Phát triển các vật liệu tiên tiến như siêu dẫn và vật liệu nano.

4.2 Ứng Dụng trong Công Nghệ Hóa Học

Trong công nghệ hóa học, năng lượng tự do Gibbs đóng vai trò quan trọng trong việc xác định tính khả thi của các phản ứng hóa học. Các quy trình sản xuất như tổng hợp phân tử, sản xuất polymer, và các phản ứng xúc tác đều yêu cầu phân tích biến thiên năng lượng tự do để tối ưu hóa hiệu suất và giảm thiểu chi phí sản xuất.

• Tính toán năng lượng tự do Gibbs để dự đoán hướng và mức độ tự phát của các phản ứng.
• Quản lý quy trình sản xuất hóa chất với hiệu quả năng lượng cao hơn.
• Áp dụng trong các ngành công nghiệp như sản xuất nhựa, dược phẩm và năng lượng tái tạo.

4.3 Ứng Dụng trong Kỹ Thuật Môi Trường

Entropy và Gibbs Free Energy có ý nghĩa đặc biệt trong kỹ thuật môi trường, khi chúng được sử dụng để phân tích và tối ưu hóa các quá trình xử lý chất thải và quản lý năng lượng. Bằng cách hiểu rõ mối quan hệ giữa năng lượng tự do và tính tự phát của các phản ứng, kỹ sư môi trường có thể cải thiện hiệu quả của các hệ thống xử lý nước, không khí và chất thải rắn.

• Ứng dụng trong quá trình xử lý sinh học và hóa học của nước thải.
• Quản lý và xử lý chất thải rắn dựa trên phân tích năng lượng tự do.
• Tối ưu hóa các quy trình sản xuất năng lượng sạch như sinh khối và pin nhiên liệu.

Entropy và năng lượng tự do Gibbs là hai đại lượng quan trọng trong việc hiểu rõ các quá trình nhiệt động lực học, đặc biệt là trong hóa học và các ngành khoa học vật liệu. Chúng có ý nghĩa lớn trong đời sống hàng ngày, từ sản xuất công nghiệp đến các quá trình tự nhiên.

• Entropy: Đây là thước đo độ hỗn loạn của hệ thống. Trong đời sống, entropy thường được liên kết với sự mất trật tự và xu hướng của các hệ thống chuyển từ trạng thái trật tự sang trạng thái hỗn loạn. Ví dụ, sự tan chảy của băng, sự bay hơi của nước đều là các quá trình có entropy tăng cao.
• Năng lượng tự do Gibbs (G): Là đại lượng dùng để dự đoán khả năng tự xảy ra của các phản ứng hóa học. Khi biến thiên năng lượng Gibbs nhỏ hơn 0, phản ứng tự xảy ra. Ứng dụng trong công nghiệp, năng lượng tự do Gibbs giúp các kỹ sư và nhà khoa học tính toán hiệu quả và tối ưu hóa các quy trình sản xuất.

Trong thực tiễn, hai đại lượng này đóng vai trò quan trọng trong:

1. Các quy trình sản xuất hóa chất: Việc tính toán biến thiên năng lượng Gibbs cho phép xác định điều kiện lý tưởng để phản ứng hóa học xảy ra, tối ưu hóa chi phí và năng suất.
2. Hệ sinh thái và môi trường: Sự thay đổi entropy có liên quan đến các hiện tượng tự nhiên như sự phân hủy của vật chất, quá trình trao đổi nhiệt và chu trình của nước trong tự nhiên.
3. Ứng dụng y học: Năng lượng tự do Gibbs được sử dụng để nghiên cứu các phản ứng sinh hóa, giúp hiểu rõ các quá trình trao đổi chất trong cơ thể và phát triển các loại thuốc hiệu quả hơn.

Tóm lại, việc nắm vững các khái niệm về entropy và năng lượng tự do Gibbs không chỉ giúp hiểu rõ hơn về các hiện tượng khoa học mà còn cung cấp công cụ hữu ích trong việc áp dụng chúng vào đời sống, từ khoa học kỹ thuật đến bảo vệ môi trường.