Chủ đề ví dụ về định luật bảo toàn năng lượng: Định luật bảo toàn năng lượng là nguyên lý quan trọng trong vật lý, giúp giải thích sự chuyển hóa năng lượng từ dạng này sang dạng khác. Bài viết này sẽ cung cấp những ví dụ điển hình, dễ hiểu về định luật bảo toàn năng lượng và ứng dụng của nó trong đời sống hàng ngày. Cùng khám phá và hiểu rõ hơn về nguyên lý cơ bản này!
Mục lục
- Định Luật Bảo Toàn Năng Lượng
- 1. Định Nghĩa Định Luật Bảo Toàn Năng Lượng
- 2. Lịch Sử Hình Thành Định Luật Bảo Toàn Năng Lượng
- 3. Các Ví Dụ Thực Tiễn Về Định Luật Bảo Toàn Năng Lượng
- 4. Ứng Dụng Của Định Luật Bảo Toàn Năng Lượng
- 5. Công Thức Toán Học Liên Quan Đến Định Luật Bảo Toàn Năng Lượng
- 6. Kết Luận Về Vai Trò Của Định Luật Bảo Toàn Năng Lượng
Định Luật Bảo Toàn Năng Lượng
Định luật bảo toàn năng lượng là một nguyên lý quan trọng trong vật lý, khẳng định rằng năng lượng không tự sinh ra hoặc mất đi mà chỉ chuyển đổi từ dạng này sang dạng khác. Đây là một trong những định luật cơ bản giúp giải thích nhiều hiện tượng tự nhiên và được ứng dụng rộng rãi trong khoa học và đời sống.
Các Ví Dụ Về Định Luật Bảo Toàn Năng Lượng
- Con lắc đơn: Khi con lắc được kéo lên và thả ra, năng lượng chuyển từ thế năng tại điểm cao nhất thành động năng khi con lắc di chuyển xuống dưới và ngược lại khi con lắc quay trở lại.
- Thí nghiệm của Joule: Thí nghiệm này chứng minh rằng cơ năng có thể chuyển thành nhiệt năng. Joule sử dụng một quả nặng để làm quay một trục gỗ, từ đó khuấy nước và tạo nhiệt.
- Dao động của lò xo: Khi một lò xo bị nén hoặc kéo giãn, năng lượng chuyển từ thế năng đàn hồi thành động năng khi lò xo dao động qua lại.
Phân Tích Định Luật Bảo Toàn Năng Lượng
Định luật bảo toàn năng lượng được minh chứng qua nhiều thí nghiệm trong thực tế. Ví dụ:
- Trong một hệ kín, tổng năng lượng là không đổi, bất kể năng lượng chuyển hóa từ dạng nào.
- Chuyển hóa năng lượng xảy ra trong các hiện tượng tự nhiên như nhiệt, cơ học và điện từ.
- Ví dụ điển hình là việc năng lượng mặt trời được chuyển hóa thành điện năng qua các tấm pin mặt trời.
Công Thức Cơ Bản Của Định Luật Bảo Toàn Năng Lượng
Công thức tổng quát của định luật bảo toàn năng lượng có thể biểu diễn như sau:
\[
E_{tổng} = E_{thế} + E_{động}
\]
Trong đó:
- \( E_{tổng} \): Tổng năng lượng của hệ
- \( E_{thế} \): Thế năng (năng lượng dự trữ khi vật ở độ cao nhất định)
- \( E_{động} \): Động năng (năng lượng vật có được khi chuyển động)
Ứng Dụng Của Định Luật Bảo Toàn Năng Lượng
Định luật bảo toàn năng lượng không chỉ giới hạn trong lý thuyết mà còn có nhiều ứng dụng thực tiễn:
| Lĩnh Vực | Ứng Dụng |
| Cơ học | Thiết kế máy móc sử dụng chuyển hóa năng lượng như động cơ ô tô, máy bay. |
| Điện học | Chuyển hóa năng lượng điện thành nhiệt năng trong các thiết bị gia dụng như máy sấy, lò vi sóng. |
| Năng lượng tái tạo | Sử dụng năng lượng mặt trời, gió để tạo ra điện năng thân thiện với môi trường. |
.png)
1. Định Nghĩa Định Luật Bảo Toàn Năng Lượng
Định luật bảo toàn năng lượng là một trong những nguyên lý cơ bản của vật lý học. Nguyên lý này khẳng định rằng tổng năng lượng của một hệ kín không thay đổi, bất kể các quá trình xảy ra trong hệ. Năng lượng không tự sinh ra hay mất đi, mà chỉ chuyển đổi từ dạng này sang dạng khác.
Để hiểu rõ hơn, chúng ta có thể xem xét từng yếu tố liên quan:
- Năng lượng: Năng lượng là khả năng thực hiện công việc hoặc sinh ra sự thay đổi trong hệ thống. Có nhiều dạng năng lượng khác nhau như động năng, thế năng, nhiệt năng, điện năng, và quang năng.
- Hệ kín: Hệ kín là hệ thống mà trong đó không có sự trao đổi năng lượng với môi trường bên ngoài. Mọi năng lượng trong hệ thống chỉ chuyển đổi từ dạng này sang dạng khác mà không có sự can thiệp bên ngoài.
Một cách toán học, định luật bảo toàn năng lượng có thể được diễn giải qua phương trình:
\[
E_{tổng} = E_{thế} + E_{động} + E_{nhiệt} + E_{điện} + E_{quang}
\]
Trong đó:
- \(E_{tổng}\): Tổng năng lượng trong hệ.
- \(E_{thế}\): Thế năng.
- \(E_{động}\): Động năng.
- \(E_{nhiệt}\): Nhiệt năng.
- \(E_{điện}\): Điện năng.
- \(E_{quang}\): Quang năng.
Định luật bảo toàn năng lượng có vai trò quan trọng trong việc giải thích các hiện tượng tự nhiên. Một số ví dụ điển hình là:
- Khi thả một vật từ trên cao, thế năng của vật chuyển thành động năng khi rơi xuống.
- Trong động cơ, năng lượng hóa học từ nhiên liệu được chuyển đổi thành động năng để di chuyển các phương tiện.
- Trong các tấm pin mặt trời, năng lượng quang của ánh sáng được chuyển đổi thành điện năng.
2. Lịch Sử Hình Thành Định Luật Bảo Toàn Năng Lượng
Định luật bảo toàn năng lượng không phải là một khái niệm được phát hiện ngay lập tức mà là kết quả của sự phát triển qua nhiều thế kỷ nghiên cứu khoa học. Dưới đây là các giai đoạn quan trọng trong lịch sử hình thành định luật này:
- Thế kỷ 17: Nhà khoa học Galileo Galilei và René Descartes đã đặt nền móng cho ý tưởng về bảo toàn động lượng trong các hệ vật lý. Descartes đã đưa ra khái niệm về "lượng chuyển động", tức là sự bảo toàn trong các va chạm giữa các vật thể.
- Thế kỷ 18: Nhà vật lý Isaac Newton đã phát triển ba định luật chuyển động, trong đó ông làm rõ sự bảo toàn động lượng và mô tả mối quan hệ giữa lực và năng lượng. Ngoài ra, nhà toán học và triết học Gottfried Wilhelm Leibniz đã nghiên cứu về động năng và thế năng, đồng thời phát triển khái niệm về "sức mạnh sống" (\(mv^2\)) mà sau này được biết đến như động năng.
- Đầu thế kỷ 19: Julius Robert von Mayer, một nhà vật lý người Đức, đã đưa ra khái niệm rằng năng lượng cơ học và năng lượng nhiệt có thể chuyển đổi lẫn nhau. Điều này dẫn đến sự hiểu biết sâu sắc hơn về sự bảo toàn năng lượng trong các hệ kín.
- 1847: Hermann von Helmholtz, một nhà vật lý và sinh lý học người Đức, chính thức phát biểu định luật bảo toàn năng lượng, dựa trên nguyên lý rằng năng lượng không thể tự sinh ra hay mất đi, mà chỉ có thể chuyển đổi từ dạng này sang dạng khác.
- Thế kỷ 20: Định luật bảo toàn năng lượng được mở rộng và xác nhận qua nhiều thí nghiệm. Các nhà khoa học như Albert Einstein đã đóng góp vào việc mở rộng định luật này sang lĩnh vực cơ học lượng tử và thuyết tương đối, với phương trình nổi tiếng \(E=mc^2\), chứng minh mối liên hệ giữa năng lượng và khối lượng.
Quá trình lịch sử này đã củng cố định luật bảo toàn năng lượng như một trong những nguyên lý cơ bản và không thể thiếu của vật lý học hiện đại.
Công thức tổng quát của định luật bảo toàn năng lượng có thể được biểu diễn qua phương trình:
\[
E_{trước} = E_{sau}
\]
Trong đó \(E\) là tổng năng lượng của hệ, luôn không đổi trong suốt quá trình.

3. Các Ví Dụ Thực Tiễn Về Định Luật Bảo Toàn Năng Lượng
Định luật bảo toàn năng lượng được áp dụng rộng rãi trong cuộc sống hàng ngày và trong nhiều ngành khoa học khác nhau. Dưới đây là một số ví dụ thực tiễn minh họa cho định luật này:
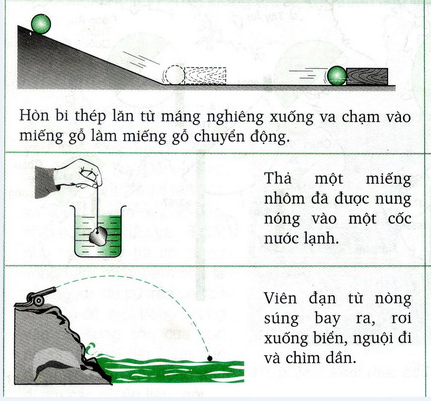
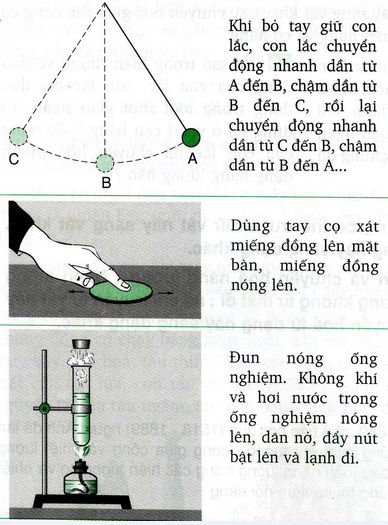
- Pendulum - Con lắc đơn: Một con lắc đơn di chuyển qua lại dưới tác động của trọng lực. Khi con lắc đạt đến điểm cao nhất, toàn bộ năng lượng của nó là thế năng. Khi nó rơi xuống, thế năng dần chuyển thành động năng. Tại điểm thấp nhất, toàn bộ năng lượng của con lắc là động năng. Tổng năng lượng của hệ (thế năng + động năng) luôn không đổi nếu không có lực ma sát.
- Bóng nảy: Khi bạn ném một quả bóng xuống đất, quả bóng rơi xuống và nảy lên. Ở điểm cao nhất, quả bóng có thế năng lớn nhất và động năng bằng 0. Khi rơi xuống, thế năng giảm dần và động năng tăng lên. Khi quả bóng chạm đất và bật lên, động năng một lần nữa chuyển đổi trở lại thành thế năng.
- Lò xo: Khi bạn kéo một lò xo và thả ra, lò xo sẽ dao động. Ở điểm kéo dài nhất, lò xo có thế năng đàn hồi cực đại. Khi nó trở về vị trí cân bằng, thế năng đàn hồi được chuyển đổi thành động năng. Quá trình chuyển đổi này tiếp diễn qua lại cho đến khi năng lượng mất dần do ma sát.
- Động cơ nhiệt: Trong động cơ ô tô, nhiên liệu cháy tạo ra năng lượng hóa học, năng lượng này sau đó chuyển đổi thành nhiệt năng và cơ năng để di chuyển xe. Mặc dù có thất thoát năng lượng dưới dạng nhiệt, nhưng tổng năng lượng trong hệ thống luôn được bảo toàn.
- Các quá trình hạt nhân: Trong phản ứng phân hạch hoặc tổng hợp hạt nhân, một phần nhỏ khối lượng được chuyển thành năng lượng theo phương trình của Einstein: \(E = mc^2\). Tổng năng lượng trước và sau phản ứng vẫn được bảo toàn, dù dưới dạng năng lượng khác nhau.
Những ví dụ trên cho thấy, trong mỗi trường hợp, năng lượng không mất đi mà chỉ chuyển từ dạng này sang dạng khác, khẳng định tính đúng đắn của định luật bảo toàn năng lượng.
Công thức cơ bản của định luật bảo toàn năng lượng là:
\[
E_{trước} = E_{sau}
\]
Với \(E\) là tổng năng lượng trong hệ, luôn không đổi trong suốt quá trình chuyển đổi năng lượng.

4. Ứng Dụng Của Định Luật Bảo Toàn Năng Lượng
Định luật bảo toàn năng lượng có nhiều ứng dụng trong khoa học, công nghệ và đời sống hàng ngày. Dưới đây là một số ứng dụng tiêu biểu của định luật này:
- Ngành công nghiệp năng lượng: Trong các nhà máy điện, năng lượng từ nhiên liệu hóa thạch hoặc năng lượng hạt nhân được chuyển hóa thành điện năng. Định luật bảo toàn năng lượng đảm bảo rằng tổng năng lượng đầu vào và đầu ra của hệ thống không đổi, dù trải qua nhiều bước chuyển đổi giữa các dạng năng lượng khác nhau như nhiệt năng, cơ năng, và điện năng.
- Công nghệ tái tạo năng lượng: Trong các hệ thống điện mặt trời, năng lượng mặt trời được chuyển thành điện năng. Định luật bảo toàn năng lượng đảm bảo rằng tổng năng lượng được hấp thụ từ ánh sáng mặt trời được chuyển thành điện năng và nhiệt năng, giúp tối ưu hóa hiệu suất của các hệ thống này.
- Động lực học trong vật lý: Định luật bảo toàn năng lượng là nguyên lý cốt lõi để tính toán các hệ thống động lực học. Ví dụ, trong việc phân tích chuyển động của vật thể trong các bài toán vật lý cơ bản, chúng ta sử dụng định luật này để xác định sự chuyển đổi giữa động năng và thế năng của hệ thống.
- Công nghệ ô tô: Trong các động cơ ô tô, nhiên liệu được đốt cháy để chuyển hóa năng lượng hóa học thành nhiệt năng và sau đó là cơ năng, giúp xe di chuyển. Các kỹ sư dựa vào định luật bảo toàn năng lượng để tối ưu hóa quá trình này, giảm thiểu thất thoát năng lượng không cần thiết.
- Hệ thống cơ học: Các hệ thống như bánh đà và con lắc sử dụng định luật bảo toàn năng lượng để duy trì chuyển động. Trong các thiết bị này, năng lượng được chuyển đổi giữa động năng và thế năng theo chu kỳ, đảm bảo hoạt động liên tục mà không bị thất thoát năng lượng đáng kể.
Các ứng dụng của định luật bảo toàn năng lượng cho phép chúng ta hiểu rõ hơn về sự vận hành của các hệ thống tự nhiên và nhân tạo. Nhờ vậy, chúng ta có thể thiết kế các công nghệ tiên tiến hơn, tối ưu hóa việc sử dụng năng lượng và giảm thiểu lãng phí.
Định luật bảo toàn năng lượng không chỉ giới hạn trong vật lý mà còn có vai trò quan trọng trong hóa học, sinh học và nhiều lĩnh vực khác. Nó giúp chúng ta hiểu rõ hơn về các quá trình tự nhiên và cải tiến các công nghệ hiện đại.

5. Công Thức Toán Học Liên Quan Đến Định Luật Bảo Toàn Năng Lượng
Định luật bảo toàn năng lượng có thể được diễn đạt dưới dạng các công thức toán học đơn giản, minh họa sự chuyển hóa và bảo toàn năng lượng trong hệ thống khép kín. Dưới đây là một số công thức tiêu biểu liên quan đến định luật này:
- Công thức tổng quát: Định luật bảo toàn năng lượng nói rằng tổng năng lượng trong một hệ thống khép kín là không đổi theo thời gian. Công thức biểu diễn như sau:
\[
E_{tổng} = E_{đầu} = E_{cuối}
\]
Trong đó:
- \( E_{tổng} \) là tổng năng lượng của hệ thống.
- \( E_{đầu} \) là năng lượng ban đầu.
- \( E_{cuối} \) là năng lượng sau quá trình chuyển đổi.
- Công thức động năng và thế năng: Trong hệ cơ học, sự bảo toàn năng lượng thường được thể hiện qua sự chuyển đổi giữa động năng và thế năng, đặc biệt trong chuyển động của vật thể:
\[
\frac{1}{2}mv^2 + mgh = hằng số
\]
Trong đó:
- \( m \) là khối lượng của vật thể.
- \( v \) là vận tốc của vật thể.
- \( g \) là gia tốc trọng trường.
- \( h \) là độ cao so với mặt đất.
- Công thức bảo toàn cơ năng: Trong hệ thống chỉ bao gồm động năng và thế năng, cơ năng tổng cộng của hệ thống là không đổi. Công thức được biểu diễn như sau:
\[
W = K + U
\]
Trong đó:
- \( W \) là cơ năng tổng cộng.
- \( K \) là động năng.
- \( U \) là thế năng.
- Công thức bảo toàn năng lượng trong nhiệt động lực học: Định luật bảo toàn năng lượng trong nhiệt động lực học thường được gọi là định luật thứ nhất của nhiệt động lực học, được biểu diễn dưới dạng:
\[
\Delta U = Q - W
\]
Trong đó:
- \( \Delta U \) là sự thay đổi nội năng của hệ thống.
- \( Q \) là nhiệt lượng cung cấp cho hệ thống.
- \( W \) là công mà hệ thống thực hiện.
Các công thức toán học này giúp chúng ta hiểu rõ hơn về cách năng lượng được bảo toàn và chuyển đổi trong các hệ thống khác nhau. Từ đó, chúng ta có thể tính toán và dự đoán chính xác các hiện tượng tự nhiên dựa trên nguyên lý bảo toàn năng lượng.
XEM THÊM:
6. Kết Luận Về Vai Trò Của Định Luật Bảo Toàn Năng Lượng
Định luật bảo toàn năng lượng là một trong những nguyên lý cơ bản của vật lý học, không chỉ giúp hiểu rõ hơn về các hiện tượng tự nhiên mà còn đóng vai trò thiết yếu trong nhiều lĩnh vực khác nhau của khoa học và đời sống. Qua các ví dụ và ứng dụng đã trình bày, có thể thấy rõ ràng rằng:
- Định luật bảo toàn năng lượng khẳng định rằng năng lượng không tự nhiên sinh ra hay mất đi, mà chỉ chuyển đổi từ dạng này sang dạng khác. Điều này giúp giải thích nhiều hiện tượng trong tự nhiên và là cơ sở cho các phát minh và ứng dụng công nghệ hiện đại.
- Trong đời sống hằng ngày, hiểu biết về định luật bảo toàn năng lượng giúp chúng ta sử dụng năng lượng một cách hiệu quả, tiết kiệm và bảo vệ môi trường. Các thiết bị tiết kiệm năng lượng, quy trình sản xuất công nghệ cao, và việc khai thác năng lượng tái tạo đều dựa trên nguyên tắc này.
- Định luật này còn là nền tảng của nhiều lĩnh vực khoa học, từ cơ học, nhiệt động lực học, đến điện từ học và thậm chí cả công nghệ năng lượng tái tạo. Các công thức toán học liên quan giúp các nhà khoa học và kỹ sư thiết kế và cải tiến các hệ thống, thiết bị với hiệu suất cao nhất.
Tóm lại, định luật bảo toàn năng lượng không chỉ là một nguyên lý vật lý trừu tượng, mà còn là chìa khóa mở ra nhiều ứng dụng quan trọng trong đời sống và khoa học. Việc hiểu rõ và áp dụng định luật này đóng vai trò quan trọng trong sự phát triển bền vững và hiệu quả của xã hội loài người.











.png)