Chủ đề công thức tính lực đàn hồi lớp 10: Công thức tính lực đàn hồi lớp 10 là nền tảng quan trọng trong chương trình vật lý, giúp học sinh hiểu rõ về lực đàn hồi và cách áp dụng trong các bài toán thực tế. Bài viết này sẽ cung cấp hướng dẫn chi tiết, ví dụ minh họa, và những ứng dụng thực tế của lực đàn hồi trong đời sống.
Mục lục
Công Thức Tính Lực Đàn Hồi Lớp 10
Trong chương trình Vật lý lớp 10, lực đàn hồi là một trong những khái niệm quan trọng, liên quan trực tiếp đến các hiện tượng vật lý trong cuộc sống hàng ngày. Dưới đây là tổng hợp các công thức tính lực đàn hồi và các ví dụ minh họa cụ thể.
I. Công Thức Tính Lực Đàn Hồi
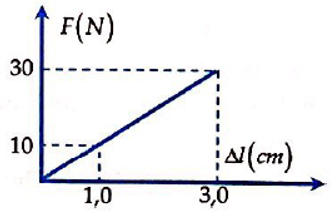
- Lực đàn hồi của lò xo được xác định theo định luật Hooke:
- Trong đó:
- \( F \) là lực đàn hồi (N)
- \( k \) là độ cứng của lò xo (N/m)
- \( \Delta l \) là độ biến dạng của lò xo so với chiều dài tự nhiên (m)
\( F = -k \times \Delta l \)
II. Đặc Điểm Và Ứng Dụng
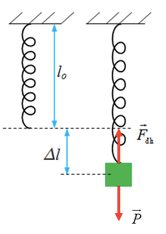
- Lực đàn hồi xuất hiện khi vật thể bị biến dạng, ví dụ như khi kéo dãn hoặc nén một lò xo.
- Độ cứng \( k \) của lò xo phụ thuộc vào vật liệu và cấu trúc của lò xo.
- Lực đàn hồi luôn có xu hướng đưa vật trở lại trạng thái cân bằng, tức là trạng thái không bị biến dạng.
III. Ví Dụ Minh Họa
Ví dụ 1: Cho một lò xo có độ cứng \( k = 100 \, \text{N/m} \), treo một vật có khối lượng \( m = 0,5 \, \text{kg} \) vào lò xo. Tính lực đàn hồi của lò xo khi nó bị kéo dãn một đoạn \( \Delta l = 5 \, \text{cm} \).
- Lời giải:
- Lực đàn hồi của lò xo là 5 N.
Sử dụng công thức: \( F = k \times \Delta l = 100 \times 0,05 = 5 \, \text{N} \).
Ví dụ 2: Một lò xo có chiều dài tự nhiên là \( 20 \, \text{cm} \). Khi treo vào một vật nặng 2 N, chiều dài của lò xo là \( 22 \, \text{cm} \). Tính độ cứng của lò xo.
- Độ cứng của lò xo là 100 N/m.
Dùng công thức \( F = k \times \Delta l \): \( 2 = k \times (0,22 - 0,20) \)
Suy ra \( k = \frac{2}{0,02} = 100 \, \text{N/m} \).
IV. Kết Luận
- Các công thức tính lực đàn hồi là nền tảng để hiểu rõ hơn về các hiện tượng vật lý như dao động, sóng, và nhiều ứng dụng thực tế khác.
- Nắm vững kiến thức về lực đàn hồi giúp học sinh vận dụng vào việc giải quyết các bài toán trong học tập và thực tế.

.png)
1. Định Luật Húc
Định luật Húc phát biểu rằng: Độ lớn của lực đàn hồi của một lò xo tỷ lệ thuận với độ biến dạng của nó. Công thức tính lực đàn hồi được biểu diễn như sau:
\[ F = -k \cdot \Delta l \]
- F: Lực đàn hồi (N)
- k: Hệ số đàn hồi của lò xo (N/m)
- \(\Delta l\): Độ biến dạng của lò xo (m)
Trong đó, dấu âm cho thấy lực đàn hồi luôn có xu hướng kéo vật trở về vị trí cân bằng ban đầu, tức là hướng ngược lại với chiều biến dạng của lò xo.
Bước đầu tiên để áp dụng định luật Húc trong bài toán thực tế là xác định các đại lượng liên quan như lực đàn hồi \(F\), độ cứng của lò xo \(k\), và độ biến dạng \(\Delta l\). Tiếp theo, sử dụng công thức trên để tính toán các giá trị cụ thể.
| Ví dụ: | Một lò xo có độ cứng \(k = 100\) N/m và bị kéo dãn một đoạn \( \Delta l = 0.05 \) m. Lực đàn hồi trong trường hợp này sẽ là: |
| \[ F = -100 \times 0.05 = -5 \text{ N} \] | |
Định luật Húc không chỉ giới hạn trong lò xo, mà còn áp dụng cho nhiều trường hợp khác như dây đàn, cầu treo, và các vật liệu có tính đàn hồi.
2. Tính Toán Lực Đàn Hồi
Để tính toán lực đàn hồi trong một hệ thống lò xo, ta cần thực hiện các bước sau:
- Xác định các thông số cần thiết: Đầu tiên, bạn cần biết hệ số đàn hồi của lò xo \(k\) (đơn vị N/m) và độ biến dạng \(\Delta l\) (đơn vị m) của lò xo khi nó bị kéo dãn hoặc nén.
- Áp dụng công thức: Sử dụng định luật Húc, lực đàn hồi được tính bằng công thức:
\[ F = -k \cdot \Delta l \]
- \(F\) là lực đàn hồi (đơn vị N).
- \(k\) là hệ số đàn hồi của lò xo (đơn vị N/m).
- \(\Delta l\) là độ biến dạng của lò xo (đơn vị m).
- Tính toán: Sau khi đã có đủ các thông số, bạn chỉ cần thay vào công thức để tính toán lực đàn hồi.
- Kiểm tra và xác nhận: Đảm bảo rằng kết quả tính toán phù hợp với thực tế và các giá trị hợp lý trong bài toán.
Ví dụ cụ thể: Giả sử bạn có một lò xo với hệ số đàn hồi \(k = 200\) N/m và lò xo bị kéo dãn một đoạn \(\Delta l = 0.1\) m. Lực đàn hồi sẽ được tính như sau:
| Bước 1: | Xác định các thông số: \(k = 200\) N/m, \(\Delta l = 0.1\) m. |
| Bước 2: | Áp dụng công thức: \[ F = -200 \times 0.1 = -20 \text{ N} \] |
| Bước 3: | Lực đàn hồi là 20 N, hướng ngược lại với chiều kéo dãn. |
Kết quả trên cho thấy lực đàn hồi có độ lớn là 20 N, và nó hướng ngược lại với lực kéo dãn lò xo. Qua các bước tính toán này, bạn có thể dễ dàng áp dụng vào các bài toán thực tế khác về lực đàn hồi.

3. Ứng Dụng Thực Tiễn
Lực đàn hồi không chỉ là một khái niệm lý thuyết mà còn có rất nhiều ứng dụng thực tiễn trong đời sống hàng ngày. Dưới đây là một số ứng dụng quan trọng của lực đàn hồi:
- Lò xo trong cơ học: Lò xo được sử dụng rộng rãi trong các hệ thống giảm chấn, hệ thống treo của xe ô tô, và nhiều thiết bị cơ khí khác. Chúng giúp hấp thụ xung lực và đảm bảo sự vận hành êm ái của các thiết bị.
- Cân lò xo: Cân lò xo là một ứng dụng tiêu biểu của định luật Húc, nơi lực đàn hồi của lò xo được sử dụng để đo khối lượng của vật thể.
- Thiết bị tập thể dục: Các dụng cụ tập thể dục như dây đàn hồi, máy chạy bộ sử dụng nguyên lý của lực đàn hồi để tạo ra sự kháng cự, giúp tăng cường sức mạnh cơ bắp.
- Cửa cuốn và rèm cuốn: Các loại cửa cuốn và rèm cuốn thường sử dụng lò xo để tạo ra lực đàn hồi, giúp chúng dễ dàng cuộn lại hoặc kéo ra.
- Đồng hồ cơ: Trong các loại đồng hồ cơ, lò xo là bộ phận quan trọng giúp duy trì hoạt động chính xác của đồng hồ thông qua lực đàn hồi.
Như vậy, lực đàn hồi và định luật Húc không chỉ đóng vai trò quan trọng trong các bài toán vật lý mà còn góp phần quan trọng trong việc phát triển các công nghệ và sản phẩm mà chúng ta sử dụng hàng ngày.

4. Các Công Thức Liên Quan
4.1. Công thức tính độ cứng của lò xo
Độ cứng của lò xo (k) là một trong những đại lượng quan trọng trong tính toán lực đàn hồi. Công thức tính độ cứng của lò xo được biểu diễn như sau:
\[ k = \frac{F}{\Delta l} \]
Trong đó:
- k: Độ cứng của lò xo (N/m)
- F: Lực đàn hồi tác dụng lên lò xo (N)
- \(\Delta l\): Độ biến dạng của lò xo (m)
4.2. Công thức tính độ biến dạng
Độ biến dạng (\(\Delta l\)) của lò xo xảy ra khi chịu tác dụng của một lực nhất định. Công thức tính độ biến dạng của lò xo được biểu diễn như sau:
\[ \Delta l = \frac{F}{k} \]
Trong đó:
- \(\Delta l\): Độ biến dạng của lò xo (m)
- F: Lực đàn hồi tác dụng lên lò xo (N)
- k: Độ cứng của lò xo (N/m)
4.3. Công thức tính lực đàn hồi cực đại
Lực đàn hồi cực đại là lực tối đa mà lò xo có thể chịu đựng trước khi mất tính đàn hồi. Công thức tính lực đàn hồi cực đại được biểu diễn như sau:
\[ F_{\text{max}} = k \cdot \Delta l_{\text{max}} \]
Trong đó:
- F_{\text{max}}: Lực đàn hồi cực đại (N)
- k: Độ cứng của lò xo (N/m)
- \(\Delta l_{\text{max}}\): Độ biến dạng cực đại mà lò xo có thể chịu đựng (m)

5. Lý Thuyết Và Bài Tập Liên Quan
Trong chương trình Vật lý lớp 10, lực đàn hồi của lò xo là một khái niệm quan trọng trong phần cơ học. Để hiểu rõ hơn về lực đàn hồi, học sinh cần nắm vững định luật Hooke và công thức tính lực đàn hồi. Dưới đây là lý thuyết cơ bản và một số dạng bài tập điển hình liên quan đến lực đàn hồi.
5.1. Lý Thuyết Cơ Bản
Lực đàn hồi là lực sinh ra khi một vật bị biến dạng do tác dụng của ngoại lực và có xu hướng đưa vật trở về trạng thái ban đầu. Đối với lò xo, lực đàn hồi tuân theo định luật Hooke và được tính theo công thức:
\[
F_{\text{đh}} = k \cdot |\Delta l|
\]
Trong đó:
- Fđh: Lực đàn hồi (N).
- k: Độ cứng của lò xo (N/m).
- \(\Delta l\): Độ biến dạng của lò xo (m).
Độ cứng của lò xo là đại lượng đặc trưng cho khả năng chống lại sự biến dạng của lò xo. Nó phụ thuộc vào vật liệu và kích thước của lò xo.
5.2. Ví Dụ Minh Họa
Ví Dụ 1: Xác Định Độ Cứng Của Lò Xo
Cho lò xo có chiều dài tự nhiên là 40 cm, khi treo vào đầu lò xo một vật có khối lượng 4 kg thì lò xo dãn ra và có chiều dài là 50 cm. Tính độ cứng của lò xo, biết gia tốc trọng trường \(g = 9,8 \, \text{m/s}^2\).
Hướng dẫn giải:
Độ biến dạng của lò xo được tính là:
\[
\Delta l = 50 - 40 = 10 \, \text{cm} = 0,1 \, \text{m}
\]
Lực đàn hồi của lò xo khi vật ở vị trí cân bằng bằng với trọng lực tác dụng lên vật:
\[
F_{\text{đh}} = P = mg = 4 \times 9,8 = 39,2 \, \text{N}
\]
Suy ra độ cứng của lò xo:
\[
k = \frac{F_{\text{đh}}}{\Delta l} = \frac{39,2}{0,1} = 392 \, \text{N/m}
\]
Ví Dụ 2: Tính Lực Đàn Hồi Khi Lò Xo Bị Nén
Một lò xo có độ cứng k = 200 N/m bị nén 0,05 m. Tính lực đàn hồi của lò xo trong trường hợp này.
Hướng dẫn giải:
Sử dụng công thức định luật Hooke:
\[
F_{\text{đh}} = k \cdot |\Delta l| = 200 \times 0,05 = 10 \, \text{N}
\]
5.3. Bài Tập Tự Luyện
- Một lò xo có chiều dài tự nhiên là 30 cm. Khi treo một vật nặng 2 kg vào đầu dưới của lò xo, lò xo dãn ra và chiều dài đạt 36 cm. Tính độ cứng của lò xo.
- Khi cắt lò xo có độ cứng k = 100 N/m thành hai đoạn bằng nhau, mỗi đoạn có độ cứng là bao nhiêu?
- Ghép hai lò xo có độ cứng lần lượt là 150 N/m và 200 N/m song song. Tính độ cứng của hệ lò xo sau khi ghép.
XEM THÊM:
6. Câu Hỏi Thường Gặp
Dưới đây là một số câu hỏi thường gặp liên quan đến lực đàn hồi và công thức tính lực đàn hồi theo định luật Húc trong chương trình Vật lý lớp 10:
- Câu hỏi 1: Lực đàn hồi là gì?
- k: Hệ số đàn hồi của vật liệu (N/m).
- Δl: Độ biến dạng của vật (m).
- Câu hỏi 2: Khi nào lực đàn hồi xuất hiện?
- Câu hỏi 3: Có những loại lực đàn hồi nào?
- Lực đàn hồi trong lò xo: Xuất hiện khi lò xo bị biến dạng.
- Lực căng: Xuất hiện khi dây cao su hoặc dây thép bị kéo dãn.
- Câu hỏi 4: Định luật Húc được áp dụng trong những trường hợp nào?
- Câu hỏi 5: Làm thế nào để tính độ cứng của lò xo?
Trả lời: Lực đàn hồi là lực xuất hiện khi một vật bị biến dạng (kéo dãn hoặc nén) và có xu hướng đưa vật trở lại trạng thái ban đầu. Độ lớn của lực đàn hồi phụ thuộc vào độ biến dạng và tính chất của vật liệu, được tính theo công thức của định luật Húc:
Trong đó:
Trả lời: Lực đàn hồi xuất hiện khi một vật bị biến dạng khỏi hình dạng ban đầu của nó, chẳng hạn như khi một lò xo bị kéo dãn hoặc nén. Lực này có phương ngược lại với lực gây biến dạng, và có xu hướng đưa vật trở về trạng thái cân bằng ban đầu.
Trả lời: Có hai loại lực đàn hồi chính:
Trả lời: Định luật Húc được áp dụng trong các trường hợp khi vật liệu đang ở trong giới hạn đàn hồi, tức là khi lực tác dụng không vượt quá một mức độ nhất định, để vật có thể trở lại hình dạng ban đầu sau khi lực tác dụng bị loại bỏ. Ngoài giới hạn này, vật liệu có thể bị biến dạng vĩnh viễn.
Trả lời: Độ cứng của lò xo (k) có thể được tính bằng cách sử dụng công thức:
Trong đó, F là lực tác dụng lên lò xo (N) và Δl là độ biến dạng của lò xo (m).