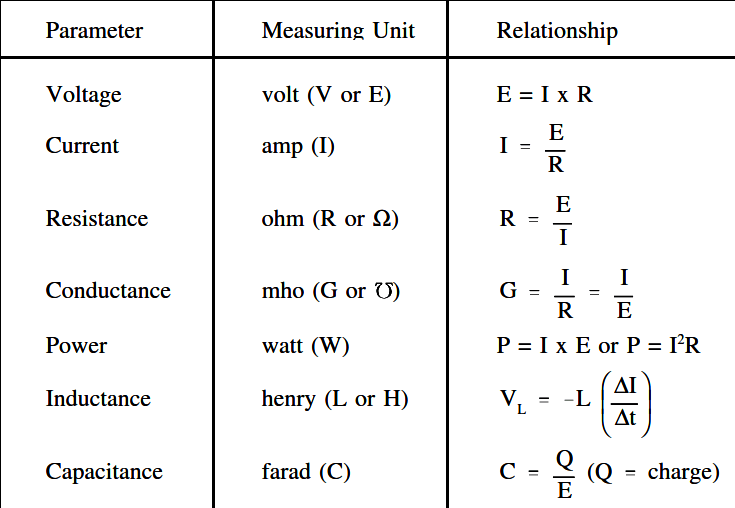Công Thức Tính Điện Tích Cực Đại: Tìm Hiểu Chi Tiết và Ứng Dụng Thực Tế

Chủ đề công thức tính điện tích cực đại: Công thức tính điện tích cực đại là một kiến thức quan trọng trong vật lý, đặc biệt là trong mạch điện và các hệ thống năng lượng. Bài viết này sẽ giúp bạn nắm vững các công thức tính toán, mối liên hệ giữa các đại lượng và cách áp dụng chúng vào thực tế một cách dễ hiểu và hiệu quả.

Mục lục

Công Thức Tính Điện Tích Cực Đại
2. Điện Tích Cực Đại Trong Mạch Điện Xoay Chiều
3. Điện Tích Cực Đại Trong Các Vật Thể Đơn Giản
4. Ví Dụ Minh Họa Và Bài Tập Thực Hành

Công Thức Tính Điện Tích Cực Đại

Điện tích cực đại là một khái niệm quan trọng trong nhiều lĩnh vực như mạch dao động LC, mạch điện xoay chiều, và các ứng dụng liên quan đến từ trường. Dưới đây là một số công thức và ví dụ minh họa về cách tính điện tích cực đại trong các trường hợp khác nhau:

1. Điện Tích Cực Đại Trong Mạch Dao Động LC

Trong mạch dao động LC gồm một cuộn cảm (L) và một tụ điện (C), điện tích cực đại \(Q_{\text{max}}\) có thể được tính như sau:

\[ Q_{\text{max}} = \sqrt{2 \cdot L \cdot W_{\text{max}}} \]

L: Độ tự cảm của cuộn cảm (Henry, H)
W_max: Năng lượng cực đại trong mạch (Joule, J)

Ví dụ: Với L = 1 \, H và W_{\text{max}} = 0.1 \, J, ta có:

\[ Q_{\text{max}} = \sqrt{2 \cdot 1 \cdot 0.1} = \sqrt{0.2} = 0.447 \, C \]

2. Điện Tích Cực Đại Trên Tụ Điện

Điện tích cực đại trên một tụ điện có điện dung C và điện áp V được tính bằng công thức:

\[ Q_{\text{max}} = C \cdot V \]

Ví dụ: Nếu C = 10 \, \mu F và V = 5 \, V, điện tích cực đại là:

\[ Q_{\text{max}} = 10 \times 10^{-6} \, F \times 5 \, V = 50 \times 10^{-6} \, C = 50 \, \mu C \]

3. Điện Tích Cực Đại Trong Mạch Điện Xoay Chiều

Trong mạch điện xoay chiều, điện tích cực đại Q_{\text{max}} có thể được tính dựa trên cường độ dòng điện cực đại I_{\text{max}} và thời gian:

\[ Q_{\text{max}} = I_{\text{max}} \cdot t \]

Ví dụ: Nếu I_{\text{max}} = 10 \, A và t = 0.1 \, s, ta có:

\[ Q_{\text{max}} = 10 \, A \times 0.1 \, s = 1 \, C \]

4. Điện Tích Cực Đại Cho Vật Thể Hình Cầu

Trong trường hợp vật thể có hình dạng đơn giản như hình cầu, điện tích cực đại có thể được tính bằng công thức:

\[ Q_{\text{max}} = 4 \pi \epsilon_0 R \]

ε₀: Hằng số điện trường trong chân không (~8.85 x 10^-12 C²/N.m²)
R: Bán kính của vật thể

Công thức này thường được áp dụng trong các bài toán liên quan đến từ trường và ứng dụng công nghiệp.

Kết Luận

Các công thức trên cung cấp các cách tính điện tích cực đại trong các bối cảnh khác nhau, giúp đảm bảo an toàn và hiệu quả trong thiết kế và vận hành hệ thống điện.

2. Điện Tích Cực Đại Trong Mạch Điện Xoay Chiều

Mạch điện xoay chiều là hệ thống trong đó dòng điện thay đổi theo thời gian và thường có dạng hình sin. Trong mạch điện xoay chiều, điện tích trên các phần tử như tụ điện và cuộn cảm cũng thay đổi liên tục. Điện tích cực đại được tính khi dòng điện hoặc hiệu điện thế đạt giá trị cực đại.

Để tính điện tích cực đại \(Q_{\text{max}}\) trong mạch điện xoay chiều, ta sử dụng công thức:

\[ Q_{\text{max}} = C \cdot U_{\text{max}} \]

C: Điện dung của tụ điện (F)
U_max: Hiệu điện thế cực đại trong mạch (V)

Trong mạch RLC nối tiếp, giá trị của điện tích cực đại cũng có thể được liên hệ với dòng điện cực đại \(I_{\text{max}}\) và tần số góc \(\omega\):

\[ Q_{\text{max}} = \frac{I_{\text{max}}}{\omega} \]

I_max: Cường độ dòng điện cực đại (A)
\(\omega\): Tần số góc, \(\omega = 2\pi f\) (rad/s)
f: Tần số của dòng điện xoay chiều (Hz)

Mối quan hệ này cho thấy điện tích cực đại không chỉ phụ thuộc vào điện dung và hiệu điện thế mà còn bị ảnh hưởng bởi tần số của dòng điện trong mạch. Điều này rất quan trọng khi thiết kế và phân tích mạch điện xoay chiều, đặc biệt là trong các hệ thống công suất lớn.

Ví dụ: Trong một mạch có \(C = 10 \, \mu F\) và \(U_{\text{max}} = 220 \, V\), điện tích cực đại sẽ là:

\[ Q_{\text{max}} = 10 \times 10^{-6} \, F \times 220 \, V = 2.2 \times 10^{-3} \, C = 2.2 \, mC \]

Hiểu rõ cách tính toán này sẽ giúp bạn điều chỉnh các tham số mạch một cách hiệu quả và đảm bảo hoạt động ổn định của hệ thống điện.

3. Điện Tích Cực Đại Trong Các Vật Thể Đơn Giản

Điện tích cực đại trong các vật thể đơn giản, như hình cầu hay hình trụ, thường được xác định dựa trên các tính chất vật lý của vật thể như điện dung và hiệu điện thế. Dưới đây là cách tính điện tích cực đại cho một số trường hợp cơ bản.

3.1 Điện Tích Cực Đại Trên Hình Cầu

Với một hình cầu dẫn điện có bán kính \(R\), điện dung của hình cầu được tính theo công thức:

\[ C = 4\pi \epsilon_0 R \]

Trong đó \(\epsilon_0\) là hằng số điện môi trong chân không.

Điện tích cực đại trên hình cầu khi hiệu điện thế giữa bề mặt hình cầu và vô cùng là \(V\) được tính theo công thức:

\[ Q_{\text{max}} = C \cdot V = 4\pi \epsilon_0 R \cdot V \]

3.2 Điện Tích Cực Đại Trên Hình Trụ

Với một hình trụ dẫn điện dài có bán kính \(r\) và chiều dài \(L\), điện tích cực đại có thể tính bằng cách xác định điện dung và hiệu điện thế:

\[ C = \frac{2\pi \epsilon_0 L}{\ln\left(\frac{D}{r}\right)} \]

Trong đó \(D\) là khoảng cách giữa trụ và mặt phẳng đối diện.

Điện tích cực đại sẽ là:

\[ Q_{\text{max}} = C \cdot V = \frac{2\pi \epsilon_0 L \cdot V}{\ln\left(\frac{D}{r}\right)} \]

3.3 Điện Tích Cực Đại Trên Mặt Phẳng Dẫn Điện

Đối với một mặt phẳng dẫn điện vô hạn, điện tích cực đại phân bố đều trên bề mặt của nó và có thể được tính thông qua mật độ điện tích:

\[ \sigma = \frac{Q_{\text{max}}}{A} = \epsilon_0 \cdot E \]

Trong đó \(A\) là diện tích bề mặt và \(E\) là cường độ điện trường.

Bằng cách áp dụng các công thức trên, bạn có thể xác định điện tích cực đại cho các vật thể có hình dạng đơn giản khác nhau. Điều này rất hữu ích trong việc thiết kế và phân tích các hệ thống điện và điện tử.

4. Ví Dụ Minh Họa Và Bài Tập Thực Hành

Để hiểu rõ hơn về cách tính điện tích cực đại trong các mạch điện và vật thể, dưới đây là một số ví dụ minh họa cùng với bài tập thực hành giúp bạn áp dụng các công thức đã học.

4.1 Ví Dụ Minh Họa

Ví dụ 1: Trong mạch dao động LC, cho biết điện dung của tụ điện là \(C = 10 \, \mu F\) và hiệu điện thế cực đại là \(U_{\text{max}} = 100 \, V\). Tính điện tích cực đại trên tụ điện.

Lời giải:

\[ Q_{\text{max}} = C \cdot U_{\text{max}} = 10 \times 10^{-6} \, F \times 100 \, V = 1 \times 10^{-3} \, C = 1 \, mC \]

Vậy, điện tích cực đại trên tụ điện là \(1 \, mC\).

Ví dụ 2: Một mạch điện xoay chiều có tần số \(f = 50 \, Hz\), điện dung của tụ điện là \(C = 5 \, \mu F\), và hiệu điện thế cực đại là \(U_{\text{max}} = 220 \, V\). Tính điện tích cực đại trên tụ điện.

Lời giải:

\[ Q_{\text{max}} = C \cdot U_{\text{max}} = 5 \times 10^{-6} \, F \times 220 \, V = 1.1 \times 10^{-3} \, C = 1.1 \, mC \]

Vậy, điện tích cực đại trên tụ điện là \(1.1 \, mC\).

4.2 Bài Tập Thực Hành

Trong một mạch dao động LC có cuộn cảm \(L = 2 \, mH\) và tụ điện \(C = 20 \, \mu F\), nếu hiệu điện thế cực đại trên tụ điện là \(U_{\text{max}} = 50 \, V\), hãy tính điện tích cực đại.
Cho mạch điện xoay chiều với tần số \(f = 60 \, Hz\) và điện dung của tụ điện là \(C = 8 \, \mu F\). Nếu dòng điện cực đại trong mạch là \(I_{\text{max}} = 0.5 \, A\), hãy tính điện tích cực đại trên tụ điện.
Một hình cầu dẫn điện có bán kính \(R = 10 \, cm\) được tích điện đến hiệu điện thế \(V = 100 \, V\). Tính điện tích cực đại trên hình cầu.

Các bài tập này sẽ giúp bạn củng cố kiến thức và khả năng tính toán điện tích cực đại trong các tình huống thực tế.