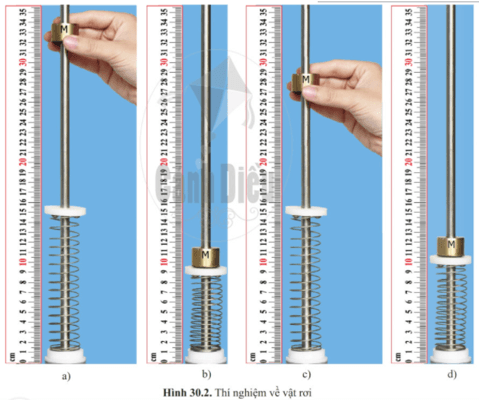
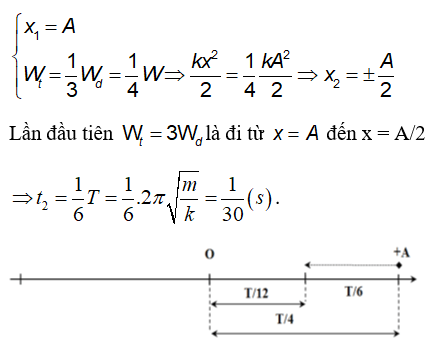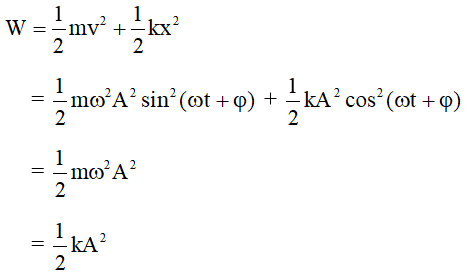Chủ đề biểu thức thế năng: Biểu thức thế năng là một khái niệm quan trọng trong vật lý học, giúp chúng ta hiểu rõ hơn về cách năng lượng hoạt động trong tự nhiên. Bài viết này sẽ giải thích chi tiết về các loại thế năng, cách tính toán và ứng dụng thực tế của chúng trong đời sống và khoa học. Hãy cùng khám phá!
Mục lục
Biểu Thức Thế Năng: Khái Niệm, Công Thức và Ứng Dụng
Thế năng là một khái niệm cơ bản trong vật lý học, đặc biệt quan trọng trong các lĩnh vực liên quan đến động lực học và cơ học. Thế năng của một vật phụ thuộc vào vị trí của nó trong một trường lực, ví dụ như trọng trường hoặc lực đàn hồi. Dưới đây là một cái nhìn chi tiết về biểu thức thế năng, công thức tính toán và ứng dụng trong thực tế.
1. Khái Niệm Thế Năng
Thế năng là dạng năng lượng mà một vật có được nhờ vị trí hoặc trạng thái của nó trong một trường lực. Có hai loại thế năng phổ biến:
- Thế năng trọng trường: Là năng lượng mà một vật có được do vị trí của nó trong trọng trường.
- Thế năng đàn hồi: Là năng lượng mà một vật có được khi bị biến dạng, chẳng hạn như kéo dãn hoặc nén lò xo.
2. Công Thức Tính Thế Năng
Thế năng được tính toán dựa trên các công thức sau:
2.1. Thế Năng Trọng Trường
Thế năng trọng trường của một vật được xác định theo công thức:
\[
W_t = m \cdot g \cdot h
\]
Trong đó:
- \( W_t \): Thế năng trọng trường (đơn vị: Joule, J)
- \( m \): Khối lượng của vật (đơn vị: kilogram, kg)
- \( g \): Gia tốc trọng trường (thường là 9.8 m/s²)
- \( h \): Độ cao của vật so với điểm mốc (đơn vị: meter, m)
2.2. Thế Năng Đàn Hồi
Thế năng đàn hồi được tính theo công thức:
\[
W_{dh} = \frac{1}{2} k \Delta l^2
\]
Trong đó:
- \( W_{dh} \): Thế năng đàn hồi (đơn vị: Joule, J)
- \( k \): Độ cứng của lò xo (đơn vị: Newton trên mét, N/m)
- \( \Delta l \): Độ biến dạng của lò xo (đơn vị: meter, m)
3. Ứng Dụng Của Thế Năng Trong Thực Tế
Thế năng có nhiều ứng dụng quan trọng trong đời sống và kỹ thuật, bao gồm:
- Thủy điện: Thế năng của nước trong các đập thủy điện được chuyển hóa thành điện năng.
- Lưu trữ năng lượng: Thế năng trọng trường được sử dụng trong các hệ thống lưu trữ năng lượng như bể nước trên cao.
- Kỹ thuật xây dựng: Tính toán thế năng được áp dụng trong thiết kế cầu, đập và các công trình xây dựng khác.
- Trò chơi và giải trí: Các trò chơi như tàu lượn siêu tốc sử dụng thế năng để tạo ra cảm giác mạnh cho người chơi.
4. Bài Tập Vận Dụng
Dưới đây là một số bài tập điển hình giúp bạn hiểu rõ hơn về cách tính và áp dụng thế năng:
- Một vật có khối lượng 2 kg được đặt ở độ cao 10 m so với mặt đất. Tính thế năng trọng trường của vật.
- Một lò xo có độ cứng 200 N/m bị kéo dãn 0,1 m. Tính thế năng đàn hồi của lò xo.
Thế năng là một trong những khái niệm cơ bản nhưng vô cùng quan trọng, giúp chúng ta hiểu sâu hơn về cách các lực và năng lượng hoạt động trong thế giới tự nhiên.

.png)
1. Giới Thiệu Về Thế Năng
Thế năng là một dạng năng lượng tồn tại trong một hệ vật lý do vị trí hoặc trạng thái của hệ đó. Khái niệm này xuất phát từ cơ học cổ điển và được sử dụng rộng rãi trong nhiều lĩnh vực khoa học. Thế năng có thể hiểu đơn giản là năng lượng "tiềm ẩn" của một vật thể trong một trường lực như trọng lực hoặc lực đàn hồi.
Trong vật lý học, thế năng thường được chia thành hai loại chính:
- Thế năng trọng trường: Thế năng này liên quan đến vị trí của một vật thể trong trường trọng lực. Ví dụ, một quả bóng nằm trên cao sẽ có thế năng trọng trường lớn hơn so với khi nó nằm trên mặt đất.
- Thế năng đàn hồi: Đây là thế năng liên quan đến sự biến dạng của một vật thể, như khi lò xo bị kéo giãn hoặc nén. Thế năng này phụ thuộc vào độ cứng của vật thể và mức độ biến dạng.
Công thức tính thế năng sẽ khác nhau tùy thuộc vào loại thế năng. Chẳng hạn, thế năng trọng trường được tính bằng công thức:
\[
W_t = m \cdot g \cdot h
\]
Trong đó:
- \(W_t\) là thế năng trọng trường
- \(m\) là khối lượng của vật thể
- \(g\) là gia tốc trọng trường (thường là 9.8 m/s²)
- \(h\) là độ cao của vật thể so với một mốc chọn trước
Thế năng đàn hồi được tính bằng công thức:
\[
W_{dh} = \frac{1}{2} k \Delta l^2
\]
Trong đó:
- \(W_{dh}\) là thế năng đàn hồi
- \(k\) là độ cứng của lò xo hoặc vật thể đàn hồi
- \(\Delta l\) là độ biến dạng của vật thể
Như vậy, thế năng là một khái niệm quan trọng giúp chúng ta hiểu rõ hơn về cách năng lượng được lưu trữ và sử dụng trong các hệ vật lý khác nhau. Nó đóng vai trò nền tảng trong việc phân tích và giải quyết nhiều vấn đề khoa học và kỹ thuật.
2. Thế Năng Trọng Trường
Thế năng trọng trường là một dạng thế năng liên quan đến vị trí của một vật thể trong trường trọng lực. Đây là năng lượng mà vật thể tích lũy được do vị trí của nó so với một điểm mốc, thường là mặt đất hoặc một điểm tham chiếu khác trong trường trọng lực.
Công thức tính thế năng trọng trường được biểu diễn như sau:
\[
W_t = m \cdot g \cdot h
\]
Trong đó:
- \(W_t\): Thế năng trọng trường (đơn vị: Joule, J)
- \(m\): Khối lượng của vật thể (đơn vị: kilogram, kg)
- \(g\): Gia tốc trọng trường (đơn vị: mét trên giây bình phương, m/s², thường là 9.8 m/s² trên Trái Đất)
- \(h\): Độ cao của vật thể so với mốc tham chiếu (đơn vị: mét, m)
Thế năng trọng trường phụ thuộc vào các yếu tố sau:
- Khối lượng của vật thể: Vật có khối lượng càng lớn thì thế năng trọng trường càng cao.
- Độ cao của vật thể: Vật càng cao so với mốc tham chiếu thì thế năng trọng trường càng lớn.
- Gia tốc trọng trường: Trên các hành tinh khác nhau, gia tốc trọng trường có thể khác nhau, dẫn đến sự thay đổi thế năng trọng trường. Trên Trái Đất, giá trị này thường được lấy là 9.8 m/s².
Ví dụ, nếu bạn nâng một vật nặng 10 kg lên độ cao 5 mét so với mặt đất, thế năng trọng trường của nó sẽ được tính như sau:
\[
W_t = 10 \cdot 9.8 \cdot 5 = 490 \, \text{Joule}
\]
Thế năng trọng trường là một khái niệm cơ bản nhưng rất quan trọng trong việc phân tích các hệ cơ học. Nó giúp chúng ta hiểu rõ hơn về cách năng lượng được lưu trữ và biến đổi khi vật thể di chuyển trong trường trọng lực. Điều này đặc biệt hữu ích trong các lĩnh vực như cơ học, kỹ thuật, và thiên văn học, nơi việc tính toán thế năng trọng trường có thể ảnh hưởng đến thiết kế và hoạt động của các hệ thống.

3. Thế Năng Đàn Hồi
Thế năng đàn hồi là năng lượng được lưu trữ trong một vật thể khi nó bị biến dạng đàn hồi, chẳng hạn như khi một lò xo bị nén hoặc kéo giãn. Đây là một dạng năng lượng tiềm ẩn, tương tự như thế năng trọng trường, nhưng nó liên quan đến lực đàn hồi thay vì lực trọng trường.
Công thức tính thế năng đàn hồi được biểu diễn như sau:
\[
W_{dh} = \frac{1}{2} k \Delta l^2
\]
Trong đó:
- \(W_{dh}\): Thế năng đàn hồi (đơn vị: Joule, J)
- \(k\): Độ cứng của lò xo hoặc hệ đàn hồi (đơn vị: Newton trên mét, N/m)
- \(\Delta l\): Độ biến dạng của vật thể so với trạng thái cân bằng (đơn vị: mét, m)
Thế năng đàn hồi phụ thuộc vào hai yếu tố chính:
- Độ cứng của vật thể: Vật có độ cứng càng lớn (giá trị \(k\) càng cao) thì thế năng đàn hồi sẽ càng lớn khi bị biến dạng.
- Độ biến dạng của vật thể: Độ biến dạng càng lớn (\(\Delta l\) càng lớn), thì thế năng đàn hồi sẽ càng lớn.
Ví dụ, khi một lò xo có độ cứng \(k = 200 \, \text{N/m}\) bị kéo giãn một khoảng \(0.1 \, \text{m}\), thế năng đàn hồi của lò xo sẽ là:
\[
W_{dh} = \frac{1}{2} \times 200 \times (0.1)^2 = 1 \, \text{Joule}
\]
Thế năng đàn hồi đóng vai trò quan trọng trong nhiều ứng dụng thực tế, chẳng hạn như trong hệ thống treo của ô tô, các loại lò xo trong đồng hồ cơ học, và nhiều thiết bị kỹ thuật khác. Hiểu rõ về thế năng đàn hồi giúp chúng ta thiết kế và tối ưu hóa các hệ thống cơ học để đảm bảo chúng hoạt động hiệu quả và an toàn.

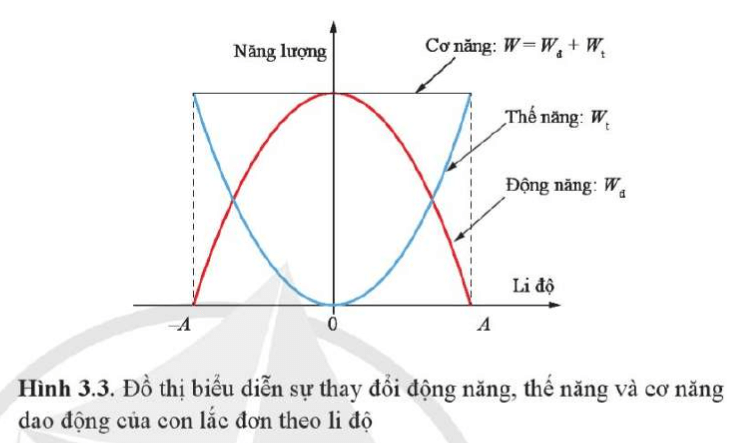
4. So Sánh Giữa Thế Năng Trọng Trường và Thế Năng Đàn Hồi
Thế năng trọng trường và thế năng đàn hồi là hai loại thế năng cơ bản trong vật lý học, mỗi loại đều liên quan đến một loại lực khác nhau và có các ứng dụng riêng biệt. Dưới đây là sự so sánh chi tiết giữa hai loại thế năng này:
| Tiêu chí | Thế Năng Trọng Trường | Thế Năng Đàn Hồi |
|---|---|---|
| Bản chất lực | Lực trọng trường, lực này tác dụng giữa các vật thể có khối lượng và kéo vật về phía tâm của hành tinh. | Lực đàn hồi, lực này xuất hiện khi một vật bị biến dạng (kéo giãn hoặc nén) và có xu hướng đưa vật trở về trạng thái cân bằng. |
| Công thức tính |
\[
W_t = m \cdot g \cdot h
\]
|
\[
W_{dh} = \frac{1}{2} k \Delta l^2
\]
|
| Phụ thuộc vào | Khối lượng của vật, gia tốc trọng trường và độ cao so với mốc tham chiếu. | Độ cứng của lò xo (hoặc vật thể) và mức độ biến dạng. |
| Ứng dụng | Được ứng dụng trong việc tính toán năng lượng của các vật thể trong chuyển động thẳng đứng, trong các bài toán liên quan đến cơ học thiên thể, và trong nhiều lĩnh vực kỹ thuật. | Được ứng dụng rộng rãi trong các hệ thống cơ khí như lò xo trong ô tô, đồng hồ cơ học, và các thiết bị kỹ thuật khác. |
| Ví dụ minh họa | Một vật nặng được nâng lên độ cao nhất định so với mặt đất, ví dụ như một quả bóng được giữ ở trên cao. | Một lò xo bị kéo giãn hoặc nén, chẳng hạn như lò xo trong bút bi hoặc trong hệ thống giảm xóc của xe. |
Qua sự so sánh trên, có thể thấy rằng mặc dù thế năng trọng trường và thế năng đàn hồi đều là các dạng năng lượng tiềm ẩn, chúng được hình thành và tính toán dựa trên các yếu tố khác nhau, phục vụ cho các mục đích nghiên cứu và ứng dụng khác nhau trong cuộc sống và kỹ thuật.

5. Các Công Thức Liên Quan Đến Thế Năng
Trong phần này, chúng ta sẽ tìm hiểu về các công thức liên quan đến thế năng, bao gồm thế năng trọng trường, thế năng đàn hồi, và các mối liên hệ giữa thế năng và công.
5.1 Công Thức Tính Thế Năng Trọng Trường
Thế năng trọng trường của một vật được xác định bởi công thức:
\( W_t = mgz \)
- \(W_t\): Thế năng trọng trường (đơn vị: Joule, J)
- \(m\): Khối lượng của vật (đơn vị: kg)
- \(g\): Gia tốc trọng trường (đơn vị: m/s²)
- \(z\): Độ cao của vật so với mốc thế năng được chọn (đơn vị: m)
5.2 Công Thức Tính Thế Năng Đàn Hồi
Thế năng đàn hồi của một lò xo có thể được tính bằng công thức:
\( W_d = \frac{1}{2}kx^2 \)
- \(W_d\): Thế năng đàn hồi (đơn vị: Joule, J)
- \(k\): Độ cứng của lò xo (đơn vị: N/m)
- \(x\): Độ biến dạng của lò xo so với vị trí cân bằng (đơn vị: m)
5.3 Liên Hệ Giữa Công và Biến Thiên Thế Năng
Khi một vật chuyển động từ vị trí này sang vị trí khác trong trọng trường, công của lực trọng trường tác dụng lên vật được tính bằng hiệu giữa thế năng tại hai vị trí đó:
\( A_{MN} = W_t(M) - W_t(N) \)
Trong đó:
- \( A_{MN} \): Công của lực trọng trường khi vật di chuyển từ M đến N
- \( W_t(M) \): Thế năng tại vị trí M
- \( W_t(N) \): Thế năng tại vị trí N
5.4 Công Thức Biến Thiên Thế Năng
Sự thay đổi thế năng khi một vật di chuyển trong trường lực được biểu diễn bằng công thức:
\( \Delta U = mgh \)
Với:
- \( \Delta U \): Biến thiên thế năng
- \( m \): Khối lượng của vật
- \( g \): Gia tốc trọng trường
- \( h \): Độ cao thay đổi của vật
5.5 Bảng Tóm Tắt Các Công Thức Thế Năng
| Công Thức | Mô Tả |
|---|---|
| \( W_t = mgz \) | Công thức tính thế năng trọng trường |
| \( W_d = \frac{1}{2}kx^2 \) | Công thức tính thế năng đàn hồi |
| \( A_{MN} = W_t(M) - W_t(N) \) | Liên hệ giữa công và biến thiên thế năng |
| \( \Delta U = mgh \) | Công thức biến thiên thế năng |
XEM THÊM:
6. Ứng Dụng Thế Năng Trong Khoa Học và Đời Sống
Thế năng không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng quan trọng trong khoa học, công nghệ và đời sống hàng ngày. Dưới đây là một số ứng dụng tiêu biểu của thế năng:
6.1 Ứng Dụng Trong Kỹ Thuật và Công Nghệ
- Nhà máy thủy điện: Thế năng của nước ở các đập cao được chuyển hóa thành động năng khi nước chảy xuống, từ đó chuyển động quay của turbine tạo ra điện năng. Đây là cách mà các nhà máy thủy điện hoạt động để cung cấp điện năng cho sinh hoạt và sản xuất công nghiệp.
- Hệ thống nâng hạ trong công nghiệp: Thế năng trọng trường được sử dụng để di chuyển hàng hóa trong kho bãi. Khi hàng hóa được nâng lên cao, thế năng của nó tăng lên, và khi hạ xuống, thế năng này được chuyển đổi lại thành các dạng năng lượng khác, giúp quá trình vận hành trở nên hiệu quả hơn.
- Máy ép thủy lực: Sử dụng thế năng đàn hồi của lò xo trong hệ thống ép để nén và ép các vật liệu. Điều này không chỉ giúp tiết kiệm năng lượng mà còn nâng cao chất lượng sản phẩm.
6.2 Ứng Dụng Trong Đời Sống Hàng Ngày
- Thể thao: Trong các môn thể thao như nhảy cầu, thế năng của vận động viên đạt đỉnh điểm khi họ ở trên cao. Khi họ nhảy xuống, thế năng này chuyển hóa thành động năng, giúp vận động viên thực hiện các động tác nhào lộn.
- Thiết bị giảm chấn: Thế năng đàn hồi được sử dụng trong các lò xo của hệ thống giảm chấn ô tô. Khi xe di chuyển trên địa hình gồ ghề, lò xo hấp thụ và giải phóng năng lượng, giúp xe di chuyển êm ái hơn.
- Hoạt động hàng ngày: Khi bạn nâng một vật lên cao, bạn đang tăng thế năng của nó. Khi thả vật xuống, thế năng này chuyển thành động năng, một hiện tượng rất phổ biến trong đời sống thường nhật mà chúng ta không hề nhận ra.

7. Bài Tập và Đề Thi Về Thế Năng
Trong phần này, chúng ta sẽ cùng tìm hiểu các dạng bài tập và đề thi thường gặp về thế năng. Các bài tập sẽ được phân loại theo mức độ khó, từ cơ bản đến nâng cao, nhằm giúp bạn nắm vững kiến thức và chuẩn bị tốt cho các kỳ thi.
7.1 Các Bài Tập Cơ Bản
- Bài tập 1: Một vật có khối lượng
\(m = 2 kg\) được nâng lên một độ cao\(h = 5 m\) so với mặt đất. Tính thế năng của vật so với mặt đất. Biết\(g = 9.8 m/s^2\) . - Bài tập 2: Từ độ cao
\(20 m\) , người ta thả rơi tự do một vật nặng. Bỏ qua sức cản không khí. Tính vận tốc của vật ngay trước khi chạm đất. - Bài tập 3: Một lò xo có độ cứng
\(k = 100 N/m\) bị nén một đoạn\(x = 0.1 m\) . Tính thế năng đàn hồi của lò xo.
7.2 Các Bài Tập Nâng Cao
- Bài tập 4: Từ độ cao
\(100 m\) , một vật có khối lượng\(m = 5 kg\) được ném thẳng đứng lên cao với vận tốc ban đầu\(v_0 = 15 m/s\) . Tính độ cao cực đại mà vật đạt được và xác định vận tốc của vật tại vị trí mà thế năng bằng động năng. - Bài tập 5: Một vật nặng
\(m = 3 kg\) được thả từ độ cao\(z_0 = 20 m\) so với mặt đất. Hỏi vật sẽ có vận tốc bao nhiêu khi chạm đất, và vận tốc này là bao nhiêu khi thế năng của vật bằng một nửa động năng?
7.3 Các Dạng Đề Thi Liên Quan Đến Thế Năng
Các dạng đề thi về thế năng thường yêu cầu học sinh tính toán và phân tích mối quan hệ giữa thế năng, động năng và các đại lượng vật lý khác. Dưới đây là một số dạng bài thường gặp:
- Dạng 1: Tính thế năng của một vật ở một độ cao nhất định so với một mốc thế năng cho trước.
- Dạng 2: Giải bài toán về sự bảo toàn cơ năng, trong đó bao gồm thế năng, động năng và cơ năng toàn phần.
- Dạng 3: Bài toán vận dụng công thức thế năng để giải quyết các bài toán thực tiễn như tính công suất máy phát điện, hoặc tính lực căng dây trong chuyển động tròn.