Biến Thiên Thế Năng: Khám Phá Cơ Chế và Ứng Dụng Thực Tiễn

Biến thiên thế năng là một khái niệm quan trọng trong vật lý, đặc biệt trong các lĩnh vực cơ học và động lực học. Khái niệm này mô tả sự thay đổi năng lượng tiềm tàng của một vật khi nó di chuyển trong trường lực, chẳng hạn như trọng trường hoặc lực đàn hồi.

1. Định nghĩa và Khái niệm Cơ bản

Thế năng là năng lượng mà một vật sở hữu do vị trí của nó trong một trường lực, chẳng hạn như trọng trường hoặc lực đàn hồi. Biến thiên thế năng là sự khác biệt giữa thế năng tại hai vị trí khác nhau khi một vật di chuyển trong trường lực đó.

2. Công thức Tính Thế Năng

Thế năng trọng trường của một vật có khối lượng \(m\) đặt ở độ cao \(h\) được tính bằng công thức:

\[
W_t = mgh
\]

Trong đó:

• \(m\) là khối lượng của vật (kg)
• \(g\) là gia tốc trọng trường (m/s²), thường lấy là 9.8 m/s² trên Trái Đất
• \(h\) là độ cao của vật so với mốc thế năng (m)

3. Biến Thiên Thế Năng

Khi một vật di chuyển từ vị trí \(M\) đến vị trí \(N\) trong trọng trường, biến thiên thế năng được xác định bằng công thức:

\[
\Delta W = W_M - W_N
\]

Nếu \(\Delta W > 0\), thế năng của vật giảm, và nếu \(\Delta W < 0\), thế năng của vật tăng.

4. Thế Năng Đàn Hồi

Thế năng đàn hồi được xác định bởi công thức:

\[
W_e = \frac{1}{2} k \Delta l^2
\]

Trong đó:

• \(k\) là độ cứng của lò xo (N/m)
• \(\Delta l\) là độ biến dạng của lò xo (m)

5. Ứng Dụng của Biến Thiên Thế Năng

Biến thiên thế năng có nhiều ứng dụng trong đời sống và kỹ thuật. Ví dụ, trong trò chơi tàu lượn siêu tốc, thế năng của toa tàu tăng khi nó được kéo lên đỉnh cao và chuyển hóa thành động năng khi nó trượt xuống. Ngoài ra, khái niệm này còn được áp dụng trong các hệ thống lò xo, máy bay, và cả trong các tính toán năng lượng trong vật lý lượng tử.

6. Ví Dụ Thực Tế

Dưới đây là một số ví dụ về cách tính biến thiên thế năng trong các tình huống thực tế:

• Một chiếc xe có khối lượng \(m = 1000 \, kg\) di chuyển từ chân đồi lên đỉnh đồi cao \(h = 50 \, m\). Biến thiên thế năng của xe là: \[ \Delta W_t = m \cdot g \cdot h = 1000 \times 9.8 \times 50 = 490000 \, J \]
• Một lò xo có độ cứng \(k = 200 \, N/m\) bị nén với độ biến dạng \(\Delta l = 0.02 \, m\). Thế năng đàn hồi của lò xo sẽ là: \[ W_e = \frac{1}{2} \times 200 \times (0.02)^2 = 0.04 \, J \]

Thế năng là một dạng năng lượng tiềm tàng được lưu trữ trong một hệ vật lý khi có sự tương tác giữa các đối tượng trong hệ. Nó phụ thuộc vào vị trí của vật trong một trường lực nhất định, chẳng hạn như trường trọng lực, trường điện từ, hoặc trường đàn hồi.

Công thức tính thế năng thường được biểu diễn dưới dạng:

\( W = m \cdot g \cdot h \)

Trong đó:

• \( W \) là thế năng (Joules)
• \( m \) là khối lượng của vật (kilogram)
• \( g \) là gia tốc trọng trường (m/s²)
• \( h \) là độ cao so với mốc chọn (meters)

Thế năng có vai trò quan trọng trong nhiều lĩnh vực, từ kỹ thuật xây dựng, cơ khí cho đến các ứng dụng năng lượng tái tạo. Việc hiểu rõ về thế năng giúp chúng ta tối ưu hóa và khai thác năng lượng một cách hiệu quả hơn.

Thế năng là một đại lượng vật lý quan trọng, nó đại diện cho năng lượng tiềm ẩn của một vật thể trong một trường lực cụ thể. Dưới đây là các công thức tính thế năng trong các trường hợp khác nhau:

2.1. Công thức tính thế năng trọng trường

Thế năng trọng trường là năng lượng mà một vật có được do vị trí của nó trong một trường trọng lực. Công thức tính như sau:

1. Trong trường hợp đơn giản với gia tốc trọng trường \(g\) không đổi, thế năng được tính bằng:

   \[ W_t = m \cdot g \cdot h \]
   • \(W_t\): Thế năng trọng trường (Joules)
   • \(m\): Khối lượng của vật (kilograms)
   • \(g\): Gia tốc trọng trường (\(9.8 \, m/s^2\))
   • \(h\): Độ cao so với mốc thế năng (meters)

2. Trong trường hợp trường trọng lực biến thiên, thế năng có thể được tính bằng cách tích phân lực trọng trường theo quãng đường:

   \[ W_t = \int_{r_1}^{r_2} F \cdot dr = - \int_{r_1}^{r_2} G \cdot \frac{m_1 \cdot m_2}{r^2} \, dr \]
   • \(G\): Hằng số hấp dẫn (\(6.674 \times 10^{-11} \, Nm^2/kg^2\))
   • \(m_1\) và \(m_2\): Khối lượng của hai vật thể (kilograms)
   • \(r\): Khoảng cách giữa hai vật thể (meters)

2.2. Công thức tính thế năng đàn hồi

Thế năng đàn hồi là năng lượng mà một vật có được do biến dạng trong một trường lực đàn hồi. Công thức tính thế năng đàn hồi là:

1. Trong trường hợp lực đàn hồi tuân theo định luật Hooke:

   \[ W_d = \frac{1}{2} k \cdot x^2 \]
   • \(W_d\): Thế năng đàn hồi (Joules)
   • \(k\): Hằng số đàn hồi của vật (N/m)
   • \(x\): Độ biến dạng của vật (meters)

2. Trong trường hợp lực đàn hồi không tuân theo định luật Hooke, thế năng có thể được tính bằng cách tích phân lực đàn hồi theo độ biến dạng:

   \[ W_d = \int_{0}^{x} F \, dx \]
   • \(F\): Lực đàn hồi (Newtons)
   • \(x\): Độ biến dạng của vật (meters)

2.3. Công thức tính thế năng trong các trường lực khác

Thế năng có thể được xác định trong các trường lực khác như trường điện, trường từ. Dưới đây là một số công thức cơ bản:

1. Trong trường hợp trường lực điện:

   \[ W_e = q \cdot V \]
   • \(W_e\): Thế năng điện (Joules)
   • \(q\): Điện tích của vật (Coulombs)
   • \(V\): Hiệu điện thế tại vị trí của vật (Volts)

2. Trong trường hợp trường lực từ:

   \[ W_m = \frac{1}{2} \cdot B^2 \cdot V/\mu \]
   • \(W_m\): Thế năng từ (Joules)
   • \(B\): Độ lớn cảm ứng từ (Tesla)
   • \(V\): Thể tích của vật (cubic meters)
   • \(\mu\): Độ từ thẩm của môi trường (Henries per meter)

Thế năng là một trong những đại lượng quan trọng trong vật lý, đặc biệt khi nghiên cứu các hệ thống dao động và chuyển động. Biến thiên của thế năng phụ thuộc vào nhiều yếu tố khác nhau, và việc hiểu rõ các yếu tố này sẽ giúp bạn nắm bắt được sự thay đổi của thế năng trong các tình huống cụ thể.

Các yếu tố ảnh hưởng đến biến thiên thế năng

• Khối lượng (m): Thế năng tỉ lệ thuận với khối lượng của vật thể. Nếu khối lượng của vật thể tăng, thế năng của nó cũng sẽ tăng tương ứng, như được thể hiện qua công thức \( U = mgh \), trong đó \( g \) là gia tốc trọng trường và \( h \) là độ cao.
• Tần số góc (ω): Trong các hệ thống dao động, tần số góc ảnh hưởng trực tiếp đến tốc độ biến thiên của thế năng. Tần số càng lớn, tốc độ biến thiên thế năng càng cao. Biến thiên này thường được thể hiện qua các hàm lượng giác như \( U(t) = \frac{1}{2} k A^2 \cos^2(\omega t + \varphi) \).
• Biên độ (A): Biên độ của dao động xác định mức độ lớn nhỏ của thế năng. Biên độ càng lớn thì thế năng cực đại càng cao, và sự biến thiên của thế năng sẽ trở nên rõ rệt hơn.
• Các lực tương tác: Các lực như lực đàn hồi, lực hấp dẫn và lực ma sát đều có tác động đáng kể đến thế năng. Ví dụ, trong một hệ dao động lò xo, thế năng đàn hồi được tính bằng \( U = \frac{1}{2} k x^2 \), trong đó \( k \) là hệ số đàn hồi và \( x \) là độ biến dạng.

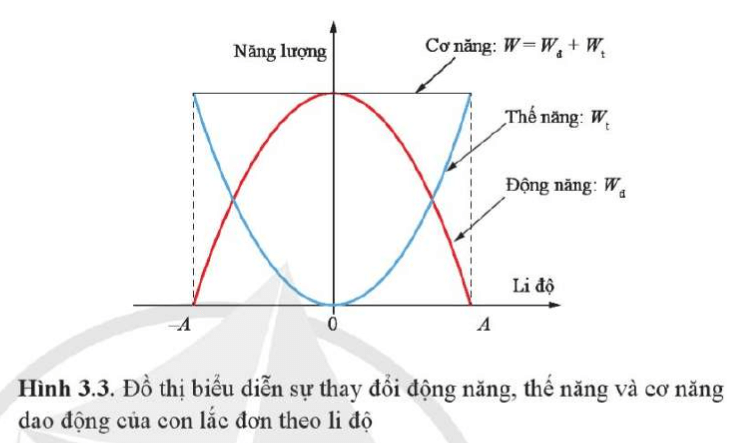
Thế năng biến thiên trong dao động điều hòa

Trong dao động điều hòa, thế năng của hệ biến thiên theo thời gian và có thể được biểu diễn bằng công thức:

\( W_T = \frac{k A^2}{4} (1 + \cos(2\omega t + 2\varphi)) \)

Điều này cho thấy thế năng biến thiên với tần số gấp đôi tần số của dao động điều hòa ban đầu. Ví dụ, nếu tần số của hệ là \( f \), thì thế năng sẽ biến thiên với tần số \( 2f \).

Biến thiên này có thể thấy rõ trong các ví dụ như con lắc đơn hay hệ dao động lò xo, nơi thế năng thay đổi một cách tuần hoàn khi vật thể di chuyển qua lại quanh vị trí cân bằng.

Kết luận

Sự biến thiên của thế năng trong các hệ thống dao động không chỉ phụ thuộc vào các yếu tố nội tại của hệ mà còn bị ảnh hưởng bởi các lực bên ngoài. Việc hiểu rõ mối quan hệ giữa thế năng và các yếu tố này giúp chúng ta phân tích và dự đoán chính xác hơn hành vi của các hệ thống vật lý.

Biến thiên thế năng là một khái niệm quan trọng trong vật lý và có nhiều ứng dụng thực tiễn trong đời sống cũng như kỹ thuật. Dưới đây là một số ứng dụng cụ thể:

• Ứng dụng trong công nghiệp: Biến thiên thế năng được sử dụng để tính toán và tối ưu hóa các quá trình liên quan đến năng lượng, chẳng hạn như trong sản xuất lò xo, ô tô, và máy bay. Trong các hệ thống này, thế năng đàn hồi của lò xo và các bộ phận đàn hồi khác giúp giảm chấn và duy trì hoạt động ổn định của máy móc.
• Ứng dụng trong đời sống hàng ngày: Một ví dụ điển hình là khi chúng ta ném một quả bóng. Thế năng đàn hồi của quả bóng sẽ bị biến dạng khi va chạm với mặt đất và sau đó chuyển hóa thành động năng, giúp bóng bật ngược lên. Tương tự, các thiết bị lưu trữ năng lượng như lò xo điện, ắc quy cũng dựa vào sự biến thiên thế năng để hoạt động hiệu quả.
• Ứng dụng trong kỹ thuật xây dựng: Biến thiên thế năng được sử dụng để dự đoán và kiểm soát sự chuyển động và năng lượng trong các công trình xây dựng, giúp đảm bảo an toàn và hiệu quả của các công trình. Ví dụ, việc thiết kế cầu đường, tòa nhà cao tầng cần tính toán kỹ lưỡng để tránh sụp đổ do biến thiên thế năng không mong muốn.
• Ứng dụng trong công nghệ năng lượng: Trong các hệ thống lưu trữ năng lượng, biến thiên thế năng được khai thác để chuyển đổi và lưu trữ năng lượng dưới dạng thế năng, sau đó chuyển hóa thành các dạng năng lượng khác khi cần thiết, giúp cải thiện hiệu suất của các hệ thống năng lượng.

Nhờ những ứng dụng đa dạng và quan trọng này, biến thiên thế năng đóng góp rất lớn vào sự phát triển của các ngành công nghiệp và nâng cao chất lượng cuộc sống hàng ngày.

Biến thiên thế năng là một khái niệm quan trọng trong vật lý, thể hiện sự thay đổi của thế năng khi một vật di chuyển trong một trường lực. Dưới đây là một số ví dụ thực tế về biến thiên thế năng trong đời sống và kỹ thuật.

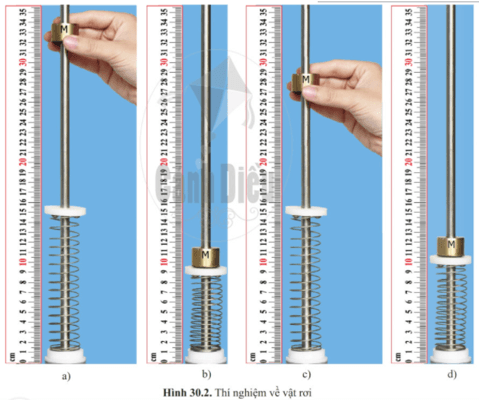
• Ví dụ 1: Thế năng trọng trường của một vật rơi tự do

  Một quả bóng có khối lượng 2 kg được thả rơi từ độ cao 10 m. Khi bóng rơi xuống, thế năng trọng trường của nó giảm dần và chuyển hóa thành động năng. Độ biến thiên thế năng của quả bóng được tính bằng công thức:

  \[\Delta W_t = mgh_1 - mgh_2\]

  Giả sử quả bóng rơi từ độ cao \(h_1 = 10\) m xuống \(h_2 = 0\) m:

  \[\Delta W_t = 2 \times 9.8 \times (10 - 0) = 196 \, J\]

  Do đó, độ biến thiên thế năng của quả bóng là 196 J.

• Ví dụ 2: Thế năng đàn hồi của lò xo

  Một lò xo có độ cứng \(k = 200 \, N/m\) bị nén một đoạn \(0.1 \, m\). Thế năng đàn hồi của lò xo khi bị nén có thể tính bằng công thức:

  \[W_{đh} = \frac{1}{2}k(\Delta l)^2\]

  Độ biến thiên thế năng đàn hồi khi lò xo thay đổi từ trạng thái không biến dạng đến khi bị nén là:

  \[\Delta W_{đh} = \frac{1}{2} \times 200 \times (0.1)^2 = 1 \, J\]

  Thế năng đàn hồi tăng thêm 1 J khi lò xo bị nén.

• Ví dụ 3: Biến thiên thế năng trong kỹ thuật xây dựng

  Trong các hệ thống cơ khí, việc tính toán biến thiên thế năng giúp đảm bảo an toàn và hiệu quả khi thiết kế cầu, thang máy, hoặc các công trình cao tầng. Ví dụ, khi tính toán lực tác động của gió lên một tòa nhà, biến thiên thế năng được sử dụng để dự đoán và điều chỉnh kết cấu, đảm bảo tòa nhà không bị dao động quá mức.

Biến thiên thế năng là một khái niệm quan trọng trong vật lý, đặc biệt trong việc giải thích và tính toán các hiện tượng tự nhiên. Dưới đây là một số bài toán phổ biến liên quan đến biến thiên thế năng, giúp bạn hiểu rõ hơn về cách áp dụng kiến thức này trong thực tế.

• Bài toán 1: Một vật có khối lượng m được nâng lên một độ cao h so với mặt đất. Tính biến thiên thế năng của vật.
• Giải:

  Biến thiên thế năng của vật được tính theo công thức:

  \[
  \Delta W = m \cdot g \cdot \Delta h
  \]

  Trong đó:

  • m là khối lượng của vật (kg)
  • g là gia tốc trọng trường (m/s²)
  • \Delta h là độ cao mà vật di chuyển (m)
• Bài toán 2: Một lò xo có độ cứng k được nén một đoạn \Delta l. Tính thế năng đàn hồi của lò xo.
• Giải:

  Thế năng đàn hồi của lò xo được tính bằng công thức:

  \[
  W_e = \frac{1}{2} k \cdot (\Delta l)^2
  \]

  Trong đó:

  • k là độ cứng của lò xo (N/m)
  • \Delta l là độ biến dạng của lò xo (m)
• Bài toán 3: Một vật rơi tự do từ độ cao h_1 xuống độ cao h_2. Tính công của trọng lực trong quá trình này.
• Giải:

  Công của trọng lực bằng biến thiên thế năng của vật, được tính theo công thức:

  \[
  A = m \cdot g \cdot (h_1 - h_2)
  \]

  Trong đó:

  • m là khối lượng của vật (kg)
  • g là gia tốc trọng trường (m/s²)
  • h_1 và h_2 lần lượt là độ cao ban đầu và độ cao sau cùng (m)