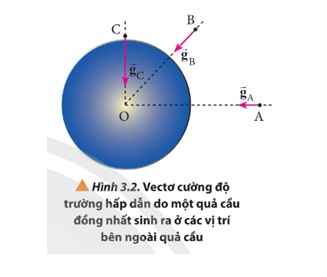
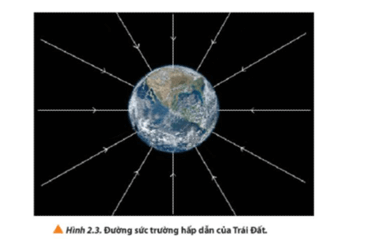
Chủ đề bài tập trường hấp dẫn: Bài tập trường hấp dẫn không chỉ giúp bạn hiểu sâu về các khái niệm vật lý mà còn nâng cao kỹ năng giải quyết vấn đề. Trong bài viết này, chúng ta sẽ cùng khám phá những bài tập hữu ích, phương pháp giải quyết và ứng dụng thực tiễn để tối ưu hóa việc học tập và nghiên cứu của bạn.
Mục lục
Bài Tập Trường Hấp Dẫn
Bài tập trường hấp dẫn là các bài tập liên quan đến lý thuyết hấp dẫn trong vật lý. Dưới đây là tổng hợp các thông tin chi tiết về bài tập này:
Các Loại Bài Tập
- Bài Tập Cơ Bản: Các bài tập này thường liên quan đến định luật vạn vật hấp dẫn của Newton, tính toán lực hấp dẫn giữa các vật thể và ứng dụng trong các tình huống cơ bản.
- Bài Tập Nâng Cao: Các bài tập nâng cao thường yêu cầu sử dụng phương trình trường hấp dẫn của Einstein trong thuyết tương đối tổng quát, và thường áp dụng trong các tình huống phức tạp hơn.
- Bài Tập Thực Hành: Những bài tập này có thể bao gồm các bài thực hành mô phỏng lực hấp dẫn trong các thiết bị thí nghiệm hoặc phần mềm mô phỏng vật lý.
Ví Dụ Cụ Thể
| Ví Dụ | Mô Tả |
|---|---|
| Tính Toán Lực Hấp Dẫn | Xác định lực hấp dẫn giữa hai vật thể có khối lượng khác nhau. |
| Ứng Dụng Thuyết Tương Đối | Giải bài toán liên quan đến hiệu ứng hấp dẫn trong thuyết tương đối tổng quát. |
Các Tài Nguyên Học Tập
Để hiểu rõ hơn về bài tập trường hấp dẫn, bạn có thể tham khảo các sách giáo khoa về vật lý, tài liệu trực tuyến, và các khóa học trực tuyến về vật lý học và thuyết tương đối.
MathJax Ví Dụ
Ví dụ về một phương trình hấp dẫn được viết bằng MathJax:
\[
F = G \frac{{m_1 m_2}}{{r^2}}
\]

.png)
1. Tổng Quan Về Bài Tập Trường Hấp Dẫn
Bài tập trường hấp dẫn là một phần quan trọng trong vật lý học, giúp chúng ta hiểu rõ hơn về lực hấp dẫn và ảnh hưởng của nó đối với các đối tượng. Dưới đây là tổng quan chi tiết về bài tập trường hấp dẫn:
- Khái Niệm Cơ Bản:
Bài tập trường hấp dẫn thường liên quan đến việc tính toán và phân tích lực hấp dẫn giữa các vật thể. Đây là một trong những khái niệm cơ bản trong vật lý, liên quan đến trọng lực và ảnh hưởng của nó đối với các vật thể có khối lượng.
- Công Thức Chính:
Công thức chính để tính lực hấp dẫn giữa hai vật thể được mô tả bằng định luật vạn vật hấp dẫn của Newton:
\[ F = G \frac{m_1 m_2}{r^2} \]
Trong đó:
- \( F \) là lực hấp dẫn giữa hai vật thể.
- \( G \) là hằng số hấp dẫn vũ trụ (khoảng \(6.674 \times 10^{-11} \, \text{m}^3 \text{kg}^{-1} \text{s}^{-2}\)).
- \( m_1 \) và \( m_2 \) là khối lượng của hai vật thể.
- \( r \) là khoảng cách giữa hai vật thể.
- Ứng Dụng Trong Bài Tập:
Bài tập trường hấp dẫn có thể bao gồm các loại bài tập như:
- Tính lực hấp dẫn giữa hai hoặc nhiều vật thể.
- Phân tích sự thay đổi lực hấp dẫn khi thay đổi khoảng cách hoặc khối lượng.
- Ứng dụng trong các bài toán thực tiễn như tính trọng lực trên các hành tinh khác nhau.
- Ví Dụ Cụ Thể:
Ví Dụ Giải Thích Tính lực hấp dẫn giữa Trái Đất và Mặt Trăng Sử dụng công thức vạn vật hấp dẫn với khối lượng của Trái Đất và Mặt Trăng cùng khoảng cách giữa chúng. Tính trọng lực trên sao Hỏa Áp dụng công thức lực hấp dẫn để tính trọng lực trên sao Hỏa dựa trên khối lượng của sao Hỏa và bán kính của nó.
2. Các Loại Bài Tập Trường Hấp Dẫn
Bài tập trường hấp dẫn được phân loại dựa trên mức độ khó khăn và loại bài toán mà chúng giải quyết. Dưới đây là các loại bài tập phổ biến trong lĩnh vực này:
- Bài Tập Cơ Bản:
Những bài tập này thường yêu cầu bạn áp dụng công thức lực hấp dẫn để tính toán các đại lượng cơ bản như lực giữa hai vật thể hoặc trọng lực của một vật trên bề mặt của hành tinh.
- Tính lực hấp dẫn giữa hai vật thể với khối lượng và khoảng cách đã cho.
- Tính trọng lực của một vật thể trên bề mặt của Trái Đất hoặc các hành tinh khác.
- Bài Tập Nâng Cao:
Những bài tập này yêu cầu bạn giải quyết các vấn đề phức tạp hơn, thường bao gồm nhiều bước tính toán hoặc áp dụng các nguyên lý nâng cao của vật lý học.
- Phân tích lực hấp dẫn trong hệ nhiều vật thể và tính tổng lực tác dụng lên một vật thể cụ thể.
- Giải các bài toán về chuyển động của vật thể dưới tác động của lực hấp dẫn không đồng đều.
- Bài Tập Ứng Dụng Thực Tiễn:
Những bài tập này liên quan đến việc áp dụng lý thuyết vào các tình huống thực tiễn, như tính toán trọng lực trên các hành tinh khác hoặc ảnh hưởng của lực hấp dẫn trong các hệ thống thiên văn học.
- Tính trọng lực trên các hành tinh khác và so sánh với trọng lực trên Trái Đất.
- Phân tích sự ảnh hưởng của lực hấp dẫn trong các hệ thống thiên văn học, như quỹ đạo của các hành tinh hoặc vệ tinh.

3. Phương Pháp Giải Bài Tập Trường Hấp Dẫn
Để giải bài tập trường hấp dẫn hiệu quả, bạn có thể áp dụng các phương pháp sau:
- Phân Tích Vấn Đề:
Bước đầu tiên là phân tích bài toán để xác định các yếu tố cần thiết như khối lượng, khoảng cách và các thông số khác. Xác định rõ ràng những gì cần tính toán và các dữ liệu đã cho.
- Áp Dụng Công Thức Cơ Bản:
Sử dụng công thức định luật vạn vật hấp dẫn của Newton để tính toán lực hấp dẫn giữa hai vật thể:
\[ F = G \frac{m_1 m_2}{r^2} \]
Trong đó:
- \( F \) là lực hấp dẫn.
- \( G \) là hằng số hấp dẫn vũ trụ.
- \( m_1 \) và \( m_2 \) là khối lượng của hai vật thể.
- \( r \) là khoảng cách giữa hai vật thể.
- Giải Quyết Các Bài Tập Phức Tạp:
Đối với các bài tập nâng cao, bạn cần áp dụng các phương pháp giải quyết phức tạp hơn, như:
- Tính toán lực hấp dẫn trong hệ nhiều vật thể bằng cách sử dụng nguyên lý tổng hợp lực.
- Giải quyết các bài toán về quỹ đạo và chuyển động của các vật thể dưới tác động của lực hấp dẫn không đồng đều.
- Kiểm Tra Kết Quả:
Sau khi tính toán, hãy kiểm tra kết quả của bạn bằng cách so sánh với các giá trị thực tế hoặc các kết quả đã biết. Đảm bảo rằng các đơn vị đo lường được sử dụng chính xác và các tính toán là hợp lý.

4. Ví Dụ và Bài Tập Thực Hành
Dưới đây là một số ví dụ và bài tập thực hành giúp bạn hiểu rõ hơn về bài tập trường hấp dẫn:
- Ví Dụ 1: Tính Lực Hấp Dẫn Giữa Hai Vật Thể
Cho hai vật thể có khối lượng \( m_1 = 5 \, \text{kg} \) và \( m_2 = 10 \, \text{kg} \), cách nhau một khoảng cách \( r = 2 \, \text{m} \). Tính lực hấp dẫn giữa chúng.
Áp dụng công thức:
\[ F = G \frac{m_1 m_2}{r^2} \]
Với \( G = 6.674 \times 10^{-11} \, \text{m}^3 \text{kg}^{-1} \text{s}^{-2} \), ta có:
\[ F = 6.674 \times 10^{-11} \frac{5 \times 10}{2^2} \approx 8.34 \times 10^{-10} \, \text{N} \]
- Ví Dụ 2: Tính Trọng Lực Trên Bề Mặt Sao Hỏa
Cho biết bán kính của sao Hỏa \( R = 3.39 \times 10^6 \, \text{m} \) và khối lượng của sao Hỏa \( M = 6.42 \times 10^{23} \, \text{kg} \). Tính trọng lực trên bề mặt sao Hỏa.
Áp dụng công thức trọng lực:
\[ g = G \frac{M}{R^2} \]
Ta có:
\[ g = 6.674 \times 10^{-11} \frac{6.42 \times 10^{23}}{(3.39 \times 10^6)^2} \approx 3.71 \, \text{m/s}^2 \]
- Bài Tập Thực Hành 1: Tính Lực Hấp Dẫn Trong Hệ Nhiều Vật Thể
Cho ba vật thể có khối lượng lần lượt là \( m_1 = 3 \, \text{kg} \), \( m_2 = 4 \, \text{kg} \) và \( m_3 = 5 \, \text{kg} \), đặt trong không gian với các khoảng cách \( r_{12} = 1 \, \text{m} \), \( r_{13} = 2 \, \text{m} \), và \( r_{23} = 1.5 \, \text{m} \). Tính tổng lực tác dụng lên \( m_1 \) do \( m_2 \) và \( m_3 \).
Sử dụng công thức và tính toán lực hấp dẫn từng cặp:
- Giữa \( m_1 \) và \( m_2 \): \[ F_{12} = G \frac{m_1 m_2}{r_{12}^2} \]
- Giữa \( m_1 \) và \( m_3 \): \[ F_{13} = G \frac{m_1 m_3}{r_{13}^2} \]
Tổng lực tác dụng lên \( m_1 \) là tổng của hai lực tính được.

5. Các Tài Nguyên và Công Cụ Hỗ Trợ
Để hỗ trợ việc học và giải quyết bài tập về trường hấp dẫn, có một số tài nguyên và công cụ hữu ích mà bạn có thể sử dụng:
- Sách Giáo Khoa và Tài Liệu Tham Khảo:
Sách giáo khoa vật lý và tài liệu tham khảo cung cấp lý thuyết cơ bản và bài tập mẫu. Một số sách nổi bật có thể kể đến:
- Sách Vật Lý Cơ Bản của các tác giả nổi tiếng.
- Tài Liệu Vật Lý Đại Cương từ các trường đại học uy tín.
- Công Cụ Tính Toán Trực Tuyến:
Các công cụ tính toán trực tuyến giúp bạn giải nhanh các bài tập về lực hấp dẫn và các vấn đề vật lý khác:
- - Công cụ tính toán mạnh mẽ cho các bài tập vật lý.
- - Công cụ đồ họa và tính toán toán học.
- Phần Mềm Mô Phỏng:
Các phần mềm mô phỏng giúp bạn hình dung rõ hơn về các hiện tượng vật lý và các bài tập:
- - Cung cấp các mô phỏng về lực hấp dẫn và các khái niệm vật lý khác.
- - Công cụ học toán học tích hợp mô phỏng và tính toán.
- Diễn Đàn và Cộng Đồng Trực Tuyến:
Tham gia các diễn đàn và cộng đồng trực tuyến để trao đổi kinh nghiệm và giải đáp thắc mắc:
- - Nơi bạn có thể hỏi và trả lời các câu hỏi về vật lý.
- - Diễn đàn thảo luận về các vấn đề vật lý.
XEM THÊM:
6. Các Xu Hướng và Nghiên Cứu Hiện Tại
Trong lĩnh vực nghiên cứu và ứng dụng bài tập trường hấp dẫn, một số xu hướng và nghiên cứu hiện tại đang được chú trọng:
- Nghiên Cứu Về Lực Hấp Dẫn Trong Các Hệ Thiên Văn Học:
Các nhà khoa học đang nghiên cứu sự ảnh hưởng của lực hấp dẫn trong các hệ thống thiên văn học phức tạp, bao gồm:
- Nghiên cứu lực hấp dẫn trong các hệ sao đôi và sao ba.
- Khám phá ảnh hưởng của lực hấp dẫn lên sự hình thành và cấu trúc của các thiên hà.
- Ứng Dụng Kỹ Thuật Mô Phỏng Số:
Các kỹ thuật mô phỏng số đang được phát triển để giải quyết các bài toán về lực hấp dẫn trong các tình huống phức tạp, bao gồm:
- Mô phỏng sự tương tác của các hạt trong các hệ nhiều vật thể.
- Phát triển các mô hình số để dự đoán hành vi của vật thể trong các môi trường khác nhau.
- Khám Phá Các Hiệu Ứng Của Lực Hấp Dẫn Trong Vật Liệu Mới:
Các nghiên cứu hiện tại cũng đang tập trung vào việc khám phá cách lực hấp dẫn ảnh hưởng đến các vật liệu mới, bao gồm:
- Ảnh hưởng của lực hấp dẫn lên các vật liệu siêu nhẹ và siêu bền.
- Nghiên cứu sự thay đổi của lực hấp dẫn trong các điều kiện môi trường cực đoan.
- Ứng Dụng Công Nghệ Vũ Trụ:
Các nghiên cứu liên quan đến lực hấp dẫn đang được áp dụng trong các dự án công nghệ vũ trụ:
- Phát triển các hệ thống định vị và đo lường lực hấp dẫn trong không gian.
- Ứng dụng lực hấp dẫn trong thiết kế các nhiệm vụ không gian và du hành vũ trụ.