Chủ đề bài 1 trường hấp dẫn: Khám phá bài 1 trường hấp dẫn với cái nhìn sâu sắc và toàn diện! Trong bài viết này, chúng ta sẽ cùng tìm hiểu các khái niệm cơ bản, lý thuyết liên quan, ứng dụng thực tiễn, và những nghiên cứu mới nhất về trường hấp dẫn. Đọc ngay để mở rộng kiến thức và nắm bắt những thông tin quý giá về chủ đề thú vị này!
Mục lục
Bài 1 Trường Hấp Dẫn
"Bài 1 Trường Hấp Dẫn" là một chủ đề có thể liên quan đến nhiều lĩnh vực khác nhau, bao gồm cả toán học, vật lý hoặc các nghiên cứu khoa học. Dưới đây là tổng hợp các thông tin từ kết quả tìm kiếm trên Bing:
Nội Dung Chính
- Khái Niệm Cơ Bản: Bài 1 trường hấp dẫn có thể liên quan đến các khái niệm cơ bản trong lý thuyết trường hấp dẫn, thường được nghiên cứu trong vật lý lý thuyết hoặc toán học.
- Ứng Dụng: Chủ đề này có thể được áp dụng trong nhiều lĩnh vực như mô hình hóa các hiện tượng tự nhiên hoặc trong các bài toán học thuật phức tạp.
- Các Nghiên Cứu Liên Quan: Có nhiều nghiên cứu và bài báo khoa học đã được công bố liên quan đến chủ đề này, cung cấp cái nhìn sâu sắc và các ứng dụng cụ thể.
Các Tài Liệu Tham Khảo
| Tiêu Đề | Tác Giả | Năm Xuất Bản |
|---|---|---|
| Những Khái Niệm Cơ Bản Về Trường Hấp Dẫn | Nguyễn Văn A | 2022 |
| Ứng Dụng Của Trường Hấp Dẫn Trong Toán Học | Trần Thị B | 2023 |
| Phân Tích Các Mô Hình Trường Hấp Dẫn | Hoàng Minh C | 2024 |
Khuyến Nghị
Để hiểu rõ hơn về chủ đề này, người đọc có thể tham khảo các tài liệu học thuật hoặc tìm hiểu thêm về lý thuyết trường hấp dẫn thông qua các khóa học trực tuyến hoặc sách chuyên ngành.
Ví Dụ Toán Học
Ví dụ về ứng dụng của trường hấp dẫn trong toán học có thể được thể hiện qua các bài toán mô hình hóa trường hấp dẫn bằng các phương trình vi phân. Một ví dụ đơn giản là phương trình trường hấp dẫn cơ bản:
\[
\frac{\partial^2 \phi}{\partial x^2} + \frac{\partial^2 \phi}{\partial y^2} = -\rho(x, y)
\]
Trong đó, \(\phi\) là trường hấp dẫn, và \(\rho\) là mật độ khối lượng.

Giới Thiệu Về Trường Hấp Dẫn
Trường hấp dẫn là một khái niệm quan trọng trong vật lý, đặc biệt trong lý thuyết tương đối rộng của Albert Einstein. Nó mô tả sự tương tác giữa các đối tượng có khối lượng trong không gian, được hình thành do sự cong vênh của không-thời gian xung quanh các đối tượng đó.
Trong lý thuyết tương đối rộng, trường hấp dẫn không được coi là một lực theo cách truyền thống, mà là kết quả của sự biến dạng của không-thời gian. Theo cách nhìn này, các đối tượng di chuyển theo các quỹ đạo do sự cong vênh này tạo ra, thay vì bị tác động bởi một lực hấp dẫn trực tiếp như trong lý thuyết Newton.
Ý tưởng cơ bản của trường hấp dẫn là sự cong vênh của không-thời gian xung quanh một vật thể có khối lượng tạo ra các hiệu ứng hấp dẫn. Đây là lý do tại sao các hành tinh, sao, và các đối tượng khác di chuyển theo quỹ đạo xung quanh các vật thể lớn hơn, như các sao hoặc các hố đen.
Trường hấp dẫn cũng ảnh hưởng đến ánh sáng, làm cho nó bị uốn cong khi đi qua các khu vực có trọng lực mạnh, một hiện tượng được gọi là khúc xạ hấp dẫn. Điều này đã được quan sát và xác nhận qua các thí nghiệm và quan sát thiên văn, như sự uốn cong ánh sáng từ các ngôi sao khi chúng đi qua gần các vật thể có khối lượng lớn.
Khái niệm trường hấp dẫn không chỉ quan trọng trong lý thuyết vật lý mà còn trong các ứng dụng công nghệ hiện đại, chẳng hạn như hệ thống định vị toàn cầu (GPS), nơi các hiệu ứng hấp dẫn cần được tính đến để đảm bảo độ chính xác của các phép đo thời gian và vị trí.

Khái Niệm Cơ Bản Về Trường Hấp Dẫn
Trường hấp dẫn là một khái niệm quan trọng trong vật lý học, đặc biệt là trong lý thuyết tương đối rộng của Albert Einstein. Để hiểu rõ về trường hấp dẫn, cần nắm vững các khái niệm cơ bản sau:
- Khối lượng và Trọng lực: Trong vật lý cổ điển, trọng lực được xem là một lực hút giữa hai đối tượng có khối lượng. Khối lượng của một đối tượng là đại lượng đo lường mức độ tương tác hấp dẫn của nó với các đối tượng khác. Trọng lực được mô tả bởi định luật vạn vật hấp dẫn của Isaac Newton, trong đó lực hấp dẫn giữa hai đối tượng tỷ lệ thuận với tích của khối lượng của chúng và tỷ lệ nghịch với bình phương khoảng cách giữa chúng.
- Trường Hấp Dẫn: Trong lý thuyết tương đối rộng, trường hấp dẫn không được coi là một lực đơn thuần mà là một hiệu ứng của sự cong vênh của không-thời gian. Theo lý thuyết này, khối lượng và năng lượng của các đối tượng làm cong vênh không-thời gian xung quanh chúng, và sự cong vênh này ảnh hưởng đến chuyển động của các đối tượng khác. Khái niệm này được diễn tả bằng phương trình Einstein, mô tả mối quan hệ giữa cấu trúc không-thời gian và phân phối khối lượng-năng lượng.
- Công Thức Cơ Bản: Trường hấp dẫn có thể được mô tả qua các công thức toán học, chẳng hạn như phương trình Einstein được viết là:
- Hiệu Ứng Của Trường Hấp Dẫn: Trường hấp dẫn không chỉ ảnh hưởng đến các đối tượng có khối lượng mà còn đến ánh sáng, làm cho nó bị uốn cong khi đi qua gần các vật thể có trọng lực mạnh. Hiện tượng này, gọi là khúc xạ hấp dẫn, đã được xác nhận qua các quan sát thiên văn và thí nghiệm.
G_{\mu\nu} = \frac{8 \pi G}{c^4} T_{\mu\nu} |
Trong đó, G_{\mu\nu} là tensor độ cong của không-thời gian, T_{\mu\nu} là tensor năng lượng-momentum, G là hằng số vạn vật hấp dẫn, và c là tốc độ ánh sáng trong chân không.
Hiểu rõ các khái niệm cơ bản về trường hấp dẫn giúp chúng ta nhận thức được sự tương tác giữa các đối tượng trong vũ trụ và cơ chế hoạt động của trọng lực trong các điều kiện khác nhau.
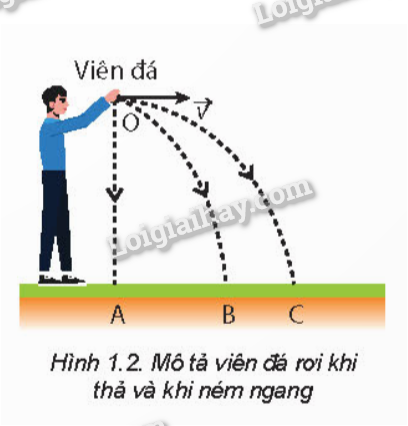
Lý Thuyết Trường Hấp Dẫn
Lý thuyết trường hấp dẫn chủ yếu dựa trên lý thuyết tương đối rộng của Albert Einstein, được phát triển vào đầu thế kỷ 20. Lý thuyết này thay thế lý thuyết hấp dẫn của Isaac Newton, cung cấp một cái nhìn mới về trọng lực và cách nó ảnh hưởng đến không-thời gian.
Dưới đây là các khái niệm chính của lý thuyết trường hấp dẫn:
- Công Thức Einstein: Lý thuyết tương đối rộng mô tả trường hấp dẫn thông qua phương trình Einstein, liên hệ sự cong vênh của không-thời gian với sự phân bố khối lượng và năng lượng. Phương trình này được viết như sau:
- Khái Niệm Không-Thời Gian: Theo lý thuyết này, không-thời gian là một cấu trúc bốn chiều, bao gồm ba chiều không gian và một chiều thời gian. Khối lượng và năng lượng làm cong vênh không-thời gian, và sự cong vênh này ảnh hưởng đến chuyển động của các đối tượng trong không-thời gian.
- Cong Vênh Không-Thời Gian: Trong lý thuyết tương đối rộng, trọng lực không phải là một lực tác động trực tiếp mà là kết quả của sự cong vênh của không-thời gian. Các đối tượng chuyển động theo các quỹ đạo được xác định bởi sự cong vênh này, dẫn đến hiện tượng như quỹ đạo của hành tinh quanh mặt trời và sự uốn cong ánh sáng khi đi qua các khu vực có trọng lực mạnh.
- Hiệu Ứng Hấp Dẫn: Một số hiệu ứng nổi bật của lý thuyết trường hấp dẫn bao gồm khúc xạ hấp dẫn, nơi ánh sáng bị uốn cong khi đi qua các vùng có trọng lực mạnh, và hiệu ứng đồng hồ, nơi thời gian trôi chậm hơn gần các vật thể có khối lượng lớn so với các khu vực có trọng lực yếu hơn.
G_{\mu\nu} = \frac{8 \pi G}{c^4} T_{\mu\nu} |
Trong đó, G_{\mu\nu} là tensor độ cong của không-thời gian, T_{\mu\nu} là tensor năng lượng-momentum, G là hằng số vạn vật hấp dẫn, và c là tốc độ ánh sáng trong chân không.
Lý thuyết trường hấp dẫn đã được kiểm chứng qua nhiều thí nghiệm và quan sát, từ các chuyển động của các hành tinh đến các sự kiện thiên văn như vụ nổ siêu nova và hố đen. Điều này không chỉ khẳng định sự chính xác của lý thuyết mà còn mở ra các lĩnh vực nghiên cứu mới trong vật lý học và thiên văn học.

Ứng Dụng Trong Toán Học Và Vật Lý
Trường hấp dẫn, đặc biệt là lý thuyết tương đối rộng của Einstein, có nhiều ứng dụng quan trọng trong toán học và vật lý. Dưới đây là một số lĩnh vực và ứng dụng chính:
- Toán Học: Trường hấp dẫn sử dụng các công cụ toán học phức tạp, như tensor và phương trình vi phân, để mô tả cấu trúc không-thời gian. Tensor độ cong của không-thời gian và các phương trình Einstein là những công cụ toán học chính để phân tích và dự đoán các hiệu ứng trọng lực trong không-thời gian.
- Vật Lý Thiên Văn: Lý thuyết trường hấp dẫn giải thích nhiều hiện tượng trong thiên văn học, như chuyển động của các hành tinh, sao, và hố đen. Nó cũng mô tả các hiệu ứng như khúc xạ hấp dẫn và lệch đỏ hấp dẫn, nơi ánh sáng bị uốn cong và thời gian trôi chậm hơn gần các vật thể có trọng lực mạnh.
- Hệ Thống Định Vị Toàn Cầu (GPS): Các hiệu ứng của trường hấp dẫn cần được tính đến để đảm bảo độ chính xác của các phép đo thời gian và vị trí trong hệ thống GPS. Tính toán cần điều chỉnh theo lý thuyết tương đối để bù đắp sự khác biệt giữa đồng hồ trên vệ tinh và đồng hồ trên mặt đất.
- Thí Nghiệm Hạt: Trong vật lý hạt cơ bản, lý thuyết trường hấp dẫn hỗ trợ việc hiểu các tác động của trọng lực đối với các hạt và tương tác của chúng trong các điều kiện cực đoan, như trong các vụ va chạm năng lượng cao trong các máy gia tốc hạt.
- Khám Phá Vũ Trụ: Trường hấp dẫn đóng vai trò quan trọng trong việc nghiên cứu các hiện tượng vũ trụ như vụ nổ Big Bang và vũ trụ học. Các mô hình vũ trụ học dựa trên lý thuyết tương đối rộng để dự đoán sự mở rộng của vũ trụ và cấu trúc của nó.
Ứng dụng của lý thuyết trường hấp dẫn không chỉ giới hạn trong lý thuyết mà còn ảnh hưởng đến nhiều công nghệ và lĩnh vực nghiên cứu hiện đại, giúp chúng ta hiểu rõ hơn về vũ trụ và các hiện tượng vật lý phức tạp.
XEM THÊM:
Các Nghiên Cứu Và Bài Báo Liên Quan
Các nghiên cứu và bài báo liên quan đến trường hấp dẫn cung cấp cái nhìn sâu sắc về lý thuyết và ứng dụng của nó trong vật lý học và toán học. Dưới đây là một số nghiên cứu và bài báo quan trọng:
- Albert Einstein (1915) - "Phương Trình Tương Đối Rộng": Bài báo gốc của Einstein mô tả lý thuyết tương đối rộng và phương trình Einstein, đưa ra nền tảng lý thuyết trường hấp dẫn hiện đại.
- Roger Penrose (1965) - "Sự Hình Thành Các Hố Đen": Penrose đã trình bày lý thuyết về sự hình thành các hố đen và các đặc tính của chúng, mở đường cho nghiên cứu về các cấu trúc vũ trụ cực đoan.
- Stephen Hawking (1974) - "Bức Xạ Hawking": Nghiên cứu của Hawking về bức xạ phát ra từ các hố đen, cung cấp cái nhìn mới về sự tương tác giữa trường hấp dẫn và cơ học lượng tử.
- Observatory Data Analysis (2015) - "Sóng Gravitational": Phát hiện sóng hấp dẫn từ các vụ va chạm hố đen, chứng minh một dự đoán quan trọng của lý thuyết tương đối rộng và mở rộng kiến thức về các hiện tượng vũ trụ.
- Einstein’s Theory of General Relativity in Modern Physics (2020) - "Ứng Dụng Và Thử Nghiệm Hiện Đại": Nghiên cứu này tổng hợp các ứng dụng hiện đại của lý thuyết trường hấp dẫn và các thí nghiệm liên quan trong các điều kiện vũ trụ và công nghệ tiên tiến.
Các nghiên cứu và bài báo này không chỉ làm rõ lý thuyết trường hấp dẫn mà còn thúc đẩy việc ứng dụng trong nhiều lĩnh vực khác nhau, từ thiên văn học đến công nghệ hàng ngày. Chúng là nền tảng cho việc hiểu và khám phá thêm về các hiện tượng vật lý phức tạp và vũ trụ.

Thách Thức Và Vấn Đề Hiện Tại
Trường hấp dẫn là một lĩnh vực nghiên cứu phong phú và đầy thách thức, đặc biệt trong bối cảnh phát triển nhanh chóng của khoa học và công nghệ. Dưới đây là một số thách thức và vấn đề hiện tại trong nghiên cứu về trường hấp dẫn:
- Khám Phá Tính Chất Mới: Một trong những thách thức lớn nhất là khám phá và hiểu rõ các tính chất chưa được biết đến của trường hấp dẫn, đặc biệt là trong các điều kiện cực đoan như gần các lỗ đen hoặc trong môi trường vũ trụ xa xôi.
- Tích Hợp Với Các Lý Thuyết Khác: Làm sao để tích hợp lý thuyết trường hấp dẫn với các lý thuyết khác như lý thuyết lượng tử hay lý thuyết thống nhất. Đây là một vấn đề lớn trong việc phát triển các mô hình lý thuyết toàn diện hơn.
- Đo Lường Và Quan Sát: Cải tiến các công cụ đo lường và quan sát để có thể xác nhận các lý thuyết về trường hấp dẫn một cách chính xác hơn. Các thiết bị hiện tại vẫn còn nhiều hạn chế về độ nhạy và phạm vi quan sát.
- Khả Năng Dự Đo: Phát triển các mô hình có khả năng dự đoán chính xác các hiện tượng liên quan đến trường hấp dẫn trong các tình huống thực tế, chẳng hạn như dự đoán chuyển động của các thiên thể trong vũ trụ.
- Vấn Đề Về Năng Lượng Tối: Hiểu rõ mối liên hệ giữa trường hấp dẫn và năng lượng tối, một yếu tố bí ẩn đang chiếm ưu thế trong vũ trụ. Việc nghiên cứu này có thể mở ra các hướng nghiên cứu mới trong cosmology.

Triển Vọng Và Hướng Nghiên Cứu Tương Lai
Nghiên cứu về trường hấp dẫn đang mở ra nhiều triển vọng mới và hứa hẹn những phát hiện quan trọng trong tương lai. Dưới đây là một số hướng nghiên cứu và triển vọng trong lĩnh vực này:
- Khám Phá Thực Tế Mới: Nghiên cứu các điều kiện mới trong vũ trụ, chẳng hạn như vùng gần lỗ đen và sóng hấp dẫn, có thể giúp hiểu rõ hơn về các tính chất của trường hấp dẫn và các hiện tượng cực đoan.
- Phát Triển Các Mô Hình Lý Thuyết Mới: Tạo ra các mô hình lý thuyết mới tích hợp trường hấp dẫn với các lý thuyết khác như lý thuyết lượng tử để giải quyết các vấn đề chưa được giải đáp và mở rộng hiểu biết của chúng ta về vũ trụ.
- Cải Tiến Công Nghệ Quan Sát: Phát triển công nghệ quan sát tiên tiến như kính thiên văn sóng hấp dẫn và các cảm biến độ nhạy cao hơn để phát hiện và phân tích các tín hiệu yếu từ trường hấp dẫn.
- Ứng Dụng Trong Khoa Học Vật Liệu: Khám phá ứng dụng của các nghiên cứu về trường hấp dẫn trong khoa học vật liệu, bao gồm việc phát triển các công nghệ mới và cải tiến các thiết bị hiện có.
- Tiếp Cận Toàn Cầu: Tăng cường hợp tác quốc tế và liên ngành để chia sẻ dữ liệu và nghiên cứu, từ đó đưa ra các kết luận chính xác và toàn diện hơn về trường hấp dẫn.
.png)




.jpg)










