Chủ đề 1 hình vuông cạnh 5cm đặt trong từ trường đều: Bài viết này sẽ khám phá chi tiết về bài toán "1 hình vuông cạnh 5cm đặt trong từ trường đều", bao gồm các công thức tính toán, phương pháp giải quyết, và ứng dụng thực tế trong lĩnh vực vật lý. Đây là nội dung hữu ích cho học sinh và những người yêu thích vật lý, giúp hiểu rõ hơn về hiện tượng cảm ứng điện từ.
Mục lục
Bài toán về hình vuông cạnh 5cm đặt trong từ trường đều
Bài toán "Một hình vuông cạnh 5cm đặt trong từ trường đều" thường xuất hiện trong các bài học và bài tập về vật lý, đặc biệt là phần điện từ học dành cho học sinh trung học phổ thông. Nội dung chính của bài toán xoay quanh việc tính toán suất điện động cảm ứng xuất hiện trong khung dây khi khung dây này quay trong từ trường.
Mô tả bài toán
Một hình vuông có cạnh 5 cm được đặt trong từ trường đều với cảm ứng từ \(\mathbf{B}\). Đường sức từ vuông góc với mặt phẳng của khung. Khi khung dây quay một góc nào đó trong thời gian nhất định, suất điện động cảm ứng được sinh ra trong khung.
Thông số cụ thể
- Kích thước khung dây: \(5 \, \text{cm} \times 5 \, \text{cm}\)
- Cảm ứng từ: Giá trị của \(\mathbf{B}\) thường được đề bài cho trước, ví dụ: \( \mathbf{B} = 0,01 \, \text{T} \)
- Thời gian quay: Thường là \(10^{-3}\) giây hoặc tương tự
Công thức liên quan
Để giải bài toán này, công thức Faraday về suất điện động cảm ứng có thể được sử dụng:
\[
\mathcal{E} = -\frac{\Delta \Phi}{\Delta t}
\]
Trong đó:
- \(\mathcal{E}\) là suất điện động cảm ứng (V)
- \(\Delta \Phi\) là độ biến thiên từ thông (Wb)
- \(\Delta t\) là khoảng thời gian quay (s)
Giá trị từ thông
Từ thông qua khung dây được tính bằng công thức:
\[
\Phi = \mathbf{B} \cdot S \cdot \cos \theta
\]
Trong đó:
- \(\mathbf{B}\) là cảm ứng từ (T)
- \(S\) là diện tích của khung dây (m2)
- \(\theta\) là góc giữa \(\mathbf{B}\) và pháp tuyến của mặt phẳng khung dây
Kết quả
Kết quả của bài toán sẽ là một giá trị cụ thể cho suất điện động cảm ứng xuất hiện trong khung dây. Đáp án thường nằm trong số các lựa chọn đã cho trước như 25 mV, 250 mV, v.v.
Ứng dụng thực tiễn
Bài toán này giúp học sinh hiểu rõ hơn về hiện tượng cảm ứng điện từ, một trong những nguyên lý cơ bản của điện học, và có thể áp dụng vào các bài toán kỹ thuật thực tế như tính toán hiệu suất của các thiết bị điện tử hoặc máy phát điện.

.png)
1. Giới thiệu về bài toán
Bài toán "1 hình vuông cạnh 5cm đặt trong từ trường đều" là một bài toán kinh điển trong vật lý phổ thông, liên quan đến hiện tượng cảm ứng điện từ. Bài toán thường được đưa ra nhằm kiểm tra hiểu biết của học sinh về các khái niệm như từ thông, cảm ứng từ, và suất điện động cảm ứng.
Bài toán được trình bày như sau: Một hình vuông có cạnh \(5 \, \text{cm}\) được đặt trong một từ trường đều có cảm ứng từ \(\mathbf{B}\). Mặt phẳng của hình vuông vuông góc với các đường sức từ. Khi hình vuông này quay một góc nào đó, từ thông qua khung dây thay đổi, dẫn đến xuất hiện suất điện động cảm ứng.
Bài toán này không chỉ đơn giản là việc áp dụng công thức, mà còn yêu cầu học sinh hiểu rõ các hiện tượng vật lý xảy ra trong quá trình biến thiên từ thông. Việc phân tích kỹ lưỡng các bước giải sẽ giúp người học nắm vững nguyên lý và ứng dụng thực tế của hiện tượng cảm ứng điện từ.
Nhờ bài toán này, học sinh có thể rèn luyện kỹ năng tư duy logic, khả năng tính toán, và hiểu biết sâu sắc hơn về một trong những hiện tượng cơ bản nhất trong điện từ học.
2. Phương pháp giải bài toán
Để giải bài toán "1 hình vuông cạnh 5cm đặt trong từ trường đều", ta cần tuân theo các bước cụ thể nhằm xác định suất điện động cảm ứng sinh ra trong khung dây khi nó quay trong từ trường. Dưới đây là các bước chi tiết:
-
Bước 1: Xác định các thông số cơ bản
- Kích thước khung dây: Diện tích hình vuông \( S = a^2 \), với \( a = 5 \, \text{cm} \), do đó \( S = 25 \, \text{cm}^2 = 25 \times 10^{-4} \, \text{m}^2 \).
- Cảm ứng từ: Cảm ứng từ \(\mathbf{B}\) có giá trị thường được đề bài cho, ví dụ \(\mathbf{B} = 0,01 \, \text{T}\).
- Góc quay: Xác định góc quay \(\theta\) giữa pháp tuyến của mặt phẳng khung dây và từ trường đều.
-
Bước 2: Tính từ thông ban đầu qua khung dây
Từ thông ban đầu \(\Phi_1\) qua khung dây khi nó chưa quay được xác định bằng công thức:
\[
\Phi_1 = \mathbf{B} \cdot S \cdot \cos(\theta_1)
\]Với \(\theta_1\) là góc giữa \(\mathbf{B}\) và pháp tuyến ban đầu của khung dây (trong nhiều bài toán, \(\theta_1\) thường bằng 0, tức là \(\cos(\theta_1) = 1\)).
-
Bước 3: Tính từ thông sau khi khung dây quay
Sau khi khung dây quay một góc \(\Delta \theta\), từ thông mới \(\Phi_2\) được xác định bằng:
\[
\Phi_2 = \mathbf{B} \cdot S \cdot \cos(\theta_2)
\]Với \(\theta_2\) là góc giữa \(\mathbf{B}\) và pháp tuyến của khung dây sau khi quay.
-
Bước 4: Tính suất điện động cảm ứng
Theo định luật Faraday, suất điện động cảm ứng \(\mathcal{E}\) sinh ra trong khung dây được tính bằng:
\[
\mathcal{E} = -\frac{\Delta \Phi}{\Delta t} = -\frac{\Phi_2 - \Phi_1}{\Delta t}
\]Trong đó, \(\Delta t\) là thời gian mà trong đó khung dây quay được một góc \(\Delta \theta\).
-
Bước 5: Tính toán và phân tích kết quả
Thực hiện tính toán các giá trị cụ thể dựa trên thông số đã cho và kiểm tra lại kết quả. Suất điện động cảm ứng tính được sẽ cho biết khả năng sinh ra dòng điện trong khung dây nếu mạch được đóng kín.
Qua các bước trên, bạn có thể hiểu rõ hơn về cách giải bài toán này và áp dụng vào các tình huống tương tự trong học tập và thực tiễn.

3. Ví dụ minh họa
Để hiểu rõ hơn về cách áp dụng phương pháp giải bài toán "1 hình vuông cạnh 5cm đặt trong từ trường đều", chúng ta sẽ đi qua một ví dụ cụ thể. Ví dụ này sẽ giúp bạn nắm vững các bước tính toán và cách áp dụng lý thuyết vào thực tế.
Ví dụ
Giả sử chúng ta có một hình vuông với cạnh \(a = 5 \, \text{cm}\) đặt trong một từ trường đều có cảm ứng từ \(\mathbf{B} = 0,02 \, \text{T}\). Mặt phẳng của hình vuông vuông góc với các đường sức từ ban đầu. Sau đó, hình vuông quay một góc \(\theta = 30^\circ\) trong thời gian \( \Delta t = 0,01 \, \text{s} \). Tính suất điện động cảm ứng sinh ra trong khung dây.
Bước 1: Tính diện tích của khung dây
Diện tích của khung dây được tính bằng:
\[
S = a^2 = (5 \, \text{cm})^2 = 25 \times 10^{-4} \, \text{m}^2
\]
Bước 2: Tính từ thông ban đầu \(\Phi_1\)
Ban đầu, góc giữa từ trường và pháp tuyến của khung dây là \(0^\circ\), do đó:
\[
\Phi_1 = \mathbf{B} \cdot S \cdot \cos(0^\circ) = 0,02 \, \text{T} \cdot 25 \times 10^{-4} \, \text{m}^2 \cdot 1 = 5 \times 10^{-5} \, \text{Wb}
\]
Bước 3: Tính từ thông sau khi quay \(\Phi_2\)
Sau khi quay góc \( \theta = 30^\circ\), từ thông qua khung dây sẽ là:
\[
\Phi_2 = \mathbf{B} \cdot S \cdot \cos(30^\circ) = 0,02 \, \text{T} \cdot 25 \times 10^{-4} \, \text{m}^2 \cdot \cos(30^\circ)
\]
Với \( \cos(30^\circ) = \frac{\sqrt{3}}{2} \), ta có:
\[
\Phi_2 = 0,02 \, \text{T} \cdot 25 \times 10^{-4} \, \text{m}^2 \cdot \frac{\sqrt{3}}{2} = 4,33 \times 10^{-5} \, \text{Wb}
\]
Bước 4: Tính suất điện động cảm ứng \(\mathcal{E}\)
Suất điện động cảm ứng được tính bằng:
\[
\mathcal{E} = -\frac{\Delta \Phi}{\Delta t} = -\frac{\Phi_2 - \Phi_1}{\Delta t} = -\frac{4,33 \times 10^{-5} \, \text{Wb} - 5 \times 10^{-5} \, \text{Wb}}{0,01 \, \text{s}}
\]
Ta tính được:
\[
\mathcal{E} = 6,7 \times 10^{-3} \, \text{V} = 6,7 \, \text{mV}
\]
Vậy suất điện động cảm ứng sinh ra trong khung dây là \( 6,7 \, \text{mV} \). Đây là kết quả cuối cùng của bài toán.
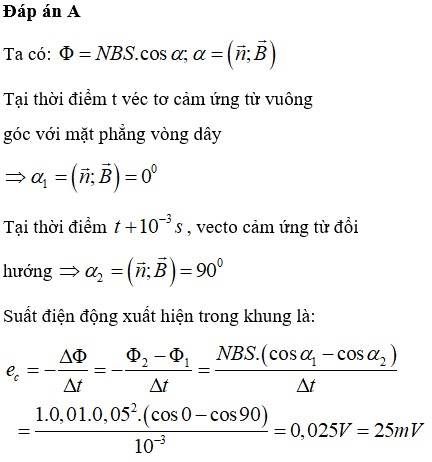
4. Câu hỏi trắc nghiệm liên quan
Dưới đây là một số câu hỏi trắc nghiệm liên quan đến bài toán "1 hình vuông cạnh 5cm đặt trong từ trường đều". Các câu hỏi này sẽ giúp bạn kiểm tra lại kiến thức và củng cố hiểu biết về hiện tượng cảm ứng điện từ.
-
Một hình vuông có cạnh 5cm được đặt trong từ trường đều có cảm ứng từ \(\mathbf{B} = 0,02 \, \text{T}\). Nếu hình vuông quay một góc \(90^\circ\) so với phương ban đầu, từ thông qua khung dây sẽ thay đổi như thế nào?
- A. Từ thông tăng lên
- B. Từ thông giảm đi
- C. Từ thông không thay đổi
- D. Không đủ thông tin để xác định
-
Suất điện động cảm ứng trong khung dây tỉ lệ thuận với yếu tố nào sau đây?
- A. Diện tích khung dây
- B. Góc quay của khung dây
- C. Thời gian thực hiện quay khung dây
- D. Tất cả các yếu tố trên
-
Khi khung dây quay từ vị trí vuông góc với từ trường sang vị trí song song với từ trường, suất điện động cảm ứng trong khung dây sẽ:
- A. Đạt giá trị cực đại
- B. Bằng không
- C. Đạt giá trị âm cực đại
- D. Không thay đổi
-
Trong bài toán "1 hình vuông cạnh 5cm đặt trong từ trường đều", nếu tăng diện tích của khung dây lên gấp đôi, suất điện động cảm ứng sẽ:
- A. Tăng gấp đôi
- B. Giảm một nửa
- C. Không thay đổi
- D. Tăng lên bốn lần
Các câu hỏi trên giúp bạn nắm vững hơn lý thuyết về cảm ứng điện từ và cách ứng dụng vào bài toán thực tế. Đừng quên luyện tập thêm để hiểu sâu hơn về các khái niệm này!

5. Các chủ đề liên quan khác
Dưới đây là một số chủ đề liên quan đến bài toán "1 hình vuông cạnh 5cm đặt trong từ trường đều" mà bạn có thể tham khảo để mở rộng kiến thức và hiểu sâu hơn về các khái niệm trong vật lý.
- Suất điện động cảm ứng: Khái niệm về suất điện động cảm ứng trong các khung dây có dạng khác nhau và ảnh hưởng của tốc độ biến thiên từ thông đến giá trị của suất điện động.
- Hiện tượng tự cảm: Tìm hiểu về hiện tượng tự cảm trong các cuộn dây và cách nó ảnh hưởng đến mạch điện trong các trường hợp khác nhau.
- Ứng dụng của từ trường trong công nghệ: Các ứng dụng thực tế của từ trường trong công nghệ hiện đại như trong máy phát điện, động cơ điện, và các thiết bị cảm biến.
- Công thức tính từ thông: Phân tích chi tiết về cách tính từ thông qua các diện tích khác nhau khi đặt trong từ trường đều và không đều.
- Bài toán khung dây trong từ trường: Nghiên cứu các bài toán khác liên quan đến khung dây đặt trong từ trường, bao gồm các dạng khung dây hình chữ nhật, hình tròn, và các cấu trúc phức tạp hơn.
- Ảnh hưởng của nhiệt độ đến từ trường: Tìm hiểu về cách nhiệt độ có thể ảnh hưởng đến tính chất của từ trường và cách các vật liệu từ tính phản ứng với sự thay đổi nhiệt độ.
Các chủ đề trên không chỉ giúp bạn củng cố kiến thức về bài toán đã học mà còn mở rộng hiểu biết về các khía cạnh khác của vật lý và ứng dụng trong cuộc sống hàng ngày.