Chủ đề xác định điện trở của một dây dẫn: Xác định điện trở của một dây dẫn là kỹ năng quan trọng trong lĩnh vực điện tử và kỹ thuật. Bài viết này cung cấp hướng dẫn chi tiết về cách tính điện trở, các yếu tố ảnh hưởng, cũng như các ứng dụng thực tế giúp bạn hiểu rõ hơn và áp dụng hiệu quả trong công việc và học tập.
Mục lục
Xác định điện trở của một dây dẫn
Việc xác định điện trở của một dây dẫn là một trong những chủ đề quan trọng trong môn Vật lý, đặc biệt liên quan đến định luật Ôm và các ứng dụng thực tiễn. Dưới đây là các thông tin chi tiết về cách xác định điện trở của dây dẫn.
1. Công thức tính điện trở của dây dẫn
Điện trở của một dây dẫn được xác định theo công thức:
\[ R = \frac{\rho \cdot L}{S} \]
Trong đó:
- \( R \): Điện trở (đơn vị: Ω)
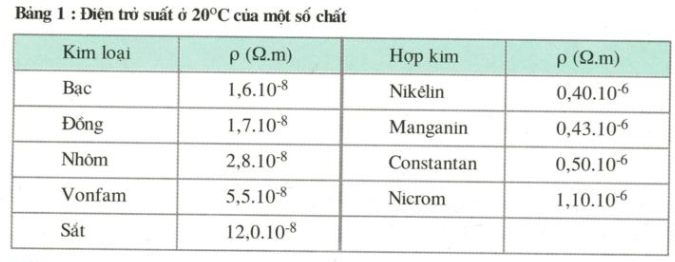
- \( \rho \): Điện trở suất của vật liệu làm dây dẫn (đơn vị: Ω·m)
- \( L \): Chiều dài dây dẫn (đơn vị: m)
- \( S \): Tiết diện ngang của dây dẫn (đơn vị: m²)
2. Phương pháp xác định điện trở thực nghiệm
Có thể xác định điện trở của dây dẫn bằng cách sử dụng ampe kế và vôn kế. Phương pháp này bao gồm các bước sau:
- Nối mạch điện gồm nguồn điện, dây dẫn cần đo, ampe kế nối tiếp với nhau, và vôn kế song song với dây dẫn.
- Đọc giá trị cường độ dòng điện \( I \) từ ampe kế và hiệu điện thế \( U \) từ vôn kế.
- Tính điện trở bằng công thức định luật Ôm:
\[ R = \frac{U}{I} \]
3. Các yếu tố ảnh hưởng đến điện trở của dây dẫn
Điện trở của một dây dẫn phụ thuộc vào các yếu tố sau:
- Chiều dài dây dẫn: Dây dẫn càng dài, điện trở càng lớn.
- Tiết diện dây dẫn: Tiết diện càng lớn, điện trở càng nhỏ.
- Vật liệu làm dây dẫn: Điện trở suất của vật liệu quyết định khả năng dẫn điện.
4. Ví dụ về bài toán tính điện trở của dây dẫn
Ví dụ: Một dây dẫn đồng có chiều dài \( 100 \)m và tiết diện ngang \( 1 \)mm². Điện trở suất của đồng là \( 1.68 \times 10^{-8} \Omega·m \). Tính điện trở của dây dẫn này:
\[ R = \frac{1.68 \times 10^{-8} \times 100}{1 \times 10^{-6}} = 0.168 \Omega \]
5. Ứng dụng trong thực tiễn
Việc tính toán điện trở giúp xác định hiệu suất truyền tải điện năng, thiết kế mạch điện, và giảm thiểu tổn thất năng lượng. Các kỹ sư có thể điều chỉnh vật liệu và cấu trúc dây dẫn để tối ưu hóa hệ thống điện.
6. Các bài tập vận dụng
Các bài tập thường yêu cầu tính toán điện trở dựa trên các thông số như chiều dài, tiết diện và vật liệu của dây dẫn. Điều này giúp học sinh hiểu rõ hơn về cách các yếu tố này ảnh hưởng đến điện trở.
| Thông số | Công thức |
|---|---|
| Điện trở | \( R = \frac{\rho \cdot L}{S} \) |
| Cường độ dòng điện | \( I = \frac{V}{R} \) |
| Hiệu điện thế | \( V = I \times R \) |
Trên đây là các thông tin chi tiết về cách xác định điện trở của dây dẫn và các yếu tố liên quan.

.png)
I. Tổng Quan Về Điện Trở Và Dây Dẫn
Điện trở là một thành phần quan trọng trong các mạch điện, đóng vai trò kiểm soát dòng điện chạy qua dây dẫn. Việc hiểu rõ về điện trở và dây dẫn giúp đảm bảo an toàn và hiệu quả trong thiết kế mạch điện.
- 1. Định Nghĩa Và Vai Trò Của Điện Trở
Điện trở \((R)\) là đại lượng vật lý đo lường khả năng cản trở dòng điện của vật liệu. Điện trở có vai trò điều tiết lượng dòng điện chạy qua mạch, bảo vệ các thiết bị điện khỏi quá tải hoặc ngắn mạch.
- 2. Các Đơn Vị Đo Điện Trở
Đơn vị đo điện trở là Ohm \((\Omega)\). Một Ohm tương đương với điện trở của một dây dẫn có dòng điện 1 Ampere chạy qua khi có hiệu điện thế 1 Volt giữa hai đầu dây dẫn.
- 3. Vai Trò Của Điện Trở Trong Thiết Kế Mạch Điện
Trong thiết kế mạch điện, điện trở được sử dụng để:
- Điều chỉnh mức dòng điện để phù hợp với yêu cầu của các thành phần trong mạch.
- Bảo vệ các thành phần điện tử khỏi dòng điện quá tải.
- Phân chia điện áp trong các mạch chia áp.
Điện trở và dây dẫn là hai yếu tố không thể thiếu trong bất kỳ mạch điện nào. Hiểu rõ về chúng giúp thiết kế và sử dụng mạch điện một cách hiệu quả và an toàn.
II. Công Thức Tính Điện Trở Của Một Dây Dẫn
Điện trở của một dây dẫn là một đại lượng vật lý biểu thị khả năng cản trở dòng điện của dây dẫn đó. Điện trở càng lớn, dòng điện đi qua dây dẫn càng nhỏ và ngược lại. Công thức tính điện trở của một dây dẫn được xác định dựa vào các yếu tố như chiều dài của dây, tiết diện của dây, và điện trở suất của vật liệu làm dây dẫn.
Điện trở \(R\) của một dây dẫn được tính theo công thức:
- \(R\): Điện trở của dây dẫn (đơn vị: Ω)
- \(\rho\): Điện trở suất của vật liệu làm dây dẫn (đơn vị: Ω·m)
- \(l\): Chiều dài của dây dẫn (đơn vị: m)
- \(S\): Tiết diện của dây dẫn (diện tích mặt cắt ngang, đơn vị: m²)
Trong đó:
- Điện trở suất \(\rho\) là một hằng số đặc trưng cho từng loại vật liệu, biểu thị khả năng cản trở dòng điện của vật liệu đó. Các vật liệu có điện trở suất cao sẽ có khả năng cản trở dòng điện tốt hơn.
- Chiều dài \(l\) của dây dẫn càng lớn thì điện trở của dây dẫn càng lớn, do điện trở tỉ lệ thuận với chiều dài.
- Tiết diện \(S\) của dây dẫn càng lớn thì điện trở càng nhỏ, do điện trở tỉ lệ nghịch với tiết diện.
Ví dụ, để tính điện trở của một dây dẫn đồng có chiều dài 5m và tiết diện 0.001m², với điện trở suất của đồng là \(1.68 \times 10^{-8} \, \Omega \cdot m\), ta có:
Công thức này cũng có thể được áp dụng để tính các thành phần khác của dây dẫn nếu biết điện trở và các thông số khác:
- Công thức tính điện trở suất: \[ \rho = \frac{R \cdot S}{l} \]
- Công thức tính chiều dài dây dẫn: \[ l = \frac{R \cdot S}{\rho} \]
- Công thức tính tiết diện dây dẫn: \[ S = \frac{\rho \cdot l}{R} \]
Những công thức này giúp bạn có thể tính toán điện trở hoặc các thông số khác của dây dẫn trong nhiều bài toán thực tế, đảm bảo hiệu suất của các mạch điện trong thiết kế và ứng dụng kỹ thuật.

III. Phương Pháp Xác Định Điện Trở Của Một Dây Dẫn
Để xác định điện trở của một dây dẫn, chúng ta có thể sử dụng phương pháp thực nghiệm với các thiết bị như ampe kế và vôn kế. Phương pháp này bao gồm các bước sau:
-
Bước 1: Chuẩn bị dụng cụ và thiết bị
- Một dây dẫn có điện trở cần xác định.
- Một nguồn điện một chiều.
- Một ampe kế để đo cường độ dòng điện chạy qua dây dẫn.
- Một vôn kế để đo hiệu điện thế giữa hai đầu dây dẫn.
- Các dây nối và công tắc điện.
-
Bước 2: Mắc mạch điện theo sơ đồ
Mắc mạch điện theo sơ đồ như sau: nối dây dẫn cần đo điện trở với nguồn điện, ampe kế mắc nối tiếp trong mạch, và vôn kế mắc song song với dây dẫn. Chú ý phân cực đúng cho ampe kế và vôn kế.
-
Bước 3: Tiến hành đo lường
Điều chỉnh nguồn điện để có các giá trị hiệu điện thế \( U \) khác nhau, ghi lại giá trị cường độ dòng điện \( I \) tương ứng đo được từ ampe kế. Lặp lại quá trình này cho nhiều giá trị \( U \) khác nhau.
-
Bước 4: Tính toán điện trở
Sử dụng công thức định luật Ôm để tính điện trở \( R \) của dây dẫn:
\[ R = \frac{U}{I} \]Trong đó:
- \( R \) là điện trở của dây dẫn (đơn vị: Ohm).
- \( U \) là hiệu điện thế đo được giữa hai đầu dây dẫn (đơn vị: Volt).
- \( I \) là cường độ dòng điện chạy qua dây dẫn (đơn vị: Ampe).
Ghi lại các giá trị điện trở tương ứng với mỗi lần đo và tính điện trở trung bình nếu cần.
-
Bước 5: Đánh giá và ghi nhận kết quả
Sau khi tính toán, so sánh các giá trị điện trở đo được để kiểm tra tính nhất quán và độ chính xác của phép đo. Ghi nhận kết quả cuối cùng vào báo cáo thực hành.
Với phương pháp này, học sinh có thể thực hành kỹ năng đo lường và tính toán điện trở của một dây dẫn một cách chính xác và hiệu quả.

IV. Ứng Dụng Của Công Thức Tính Điện Trở
Công thức tính điện trở của một dây dẫn không chỉ mang tính lý thuyết mà còn có nhiều ứng dụng thực tiễn trong đời sống và công nghiệp. Dưới đây là một số ứng dụng quan trọng của công thức này:
1. Thiết Kế Mạch Điện An Toàn Và Hiệu Quả
Trong thiết kế mạch điện, việc xác định chính xác điện trở của các thành phần giúp đảm bảo rằng dòng điện chạy qua mạch không vượt quá mức an toàn. Công thức tính điện trở \( R = \frac{U}{I} \) cho phép kỹ sư điều chỉnh giá trị điện trở để đảm bảo hiệu suất tối ưu và an toàn cho người sử dụng.
2. Ứng Dụng Trong Sản Xuất Và Bảo Trì
Điện trở suất của vật liệu là yếu tố quan trọng trong việc sản xuất các thiết bị điện tử và dây dẫn. Công thức \( R = \rho \frac{L}{A} \) giúp các nhà sản xuất lựa chọn vật liệu phù hợp với điện trở mong muốn, đảm bảo chất lượng và độ bền của sản phẩm. Ngoài ra, trong quá trình bảo trì, việc đo lường và kiểm tra điện trở giúp xác định tình trạng hoạt động của các thiết bị điện, từ đó có biện pháp sửa chữa kịp thời.
3. Phát Triển Vật Liệu Mới Với Điện Trở Tối Ưu
Công thức tính điện trở còn đóng vai trò quan trọng trong nghiên cứu và phát triển vật liệu mới. Bằng cách thay đổi các yếu tố như độ dài \(L\), diện tích tiết diện \(A\), và điện trở suất \( \rho \), các nhà khoa học có thể tạo ra vật liệu với điện trở suất tối ưu cho các ứng dụng cụ thể, từ đó nâng cao hiệu quả và tiết kiệm năng lượng trong các hệ thống điện.
Như vậy, công thức tính điện trở không chỉ giúp xác định giá trị điện trở của một dây dẫn mà còn mở ra nhiều ứng dụng quan trọng trong các lĩnh vực khác nhau, từ thiết kế, sản xuất đến nghiên cứu và phát triển.

V. Bài Tập Thực Hành Và Ví Dụ Minh Họa
Dưới đây là các bài tập và ví dụ minh họa giúp bạn nắm vững cách tính toán và xác định điện trở của một dây dẫn dựa trên các thông số như chiều dài, tiết diện ngang và điện trở suất của vật liệu.
1. Bài Tập Thực Hành
-
Một dây dẫn bằng đồng có chiều dài \(L = 100\, \text{m}\), tiết diện ngang \(A = 1\, \text{mm}^2\). Biết điện trở suất của đồng là \(\rho = 1.68 \times 10^{-8}\, \Omega \cdot \text{m}\). Hãy tính điện trở \(R\) của dây dẫn này.
Hướng dẫn:
Áp dụng công thức:
\[
R = \rho \frac{L}{A}
\]Trong đó:
- \(R\) là điện trở của dây dẫn (đơn vị: \(\Omega\)).
- \(\rho\) là điện trở suất của vật liệu (đơn vị: \(\Omega \cdot \text{m}\)).
- \(L\) là chiều dài dây dẫn (đơn vị: \(\text{m}\)).
- \(A\) là tiết diện ngang của dây (đơn vị: \(\text{m}^2\)).
Thay các giá trị đã cho vào công thức:
\[
R = 1.68 \times 10^{-8} \times \frac{100}{1 \times 10^{-6}} = 1.68\, \Omega
\]Vậy điện trở của dây dẫn là \(1.68\, \Omega\).
-
Một dây dẫn nhôm có chiều dài \(L = 200\, \text{m}\) và tiết diện ngang \(A = 0.5\, \text{mm}^2\). Biết điện trở suất của nhôm là \(\rho = 2.82 \times 10^{-8}\, \Omega \cdot \text{m}\). Hãy xác định điện trở \(R\) của dây dẫn này.
Hướng dẫn:
Áp dụng tương tự công thức trên:
\[
R = \rho \frac{L}{A}
\]Thay các giá trị vào:
\[
R = 2.82 \times 10^{-8} \times \frac{200}{0.5 \times 10^{-6}} = 11.28\, \Omega
\]Vậy điện trở của dây dẫn là \(11.28\, \Omega\).
2. Ví Dụ Minh Họa
Hãy xem xét một tình huống thực tế: Bạn cần thiết kế một mạch điện với yêu cầu dây dẫn phải có điện trở không vượt quá \(5\, \Omega\). Bạn có thể sử dụng dây dẫn bằng nhôm với chiều dài \(L = 50\, \text{m}\). Tiết diện ngang của dây dẫn cần phải như thế nào?
Giải:
Sử dụng lại công thức:
\[
R = \rho \frac{L}{A} \quad \Rightarrow \quad A = \rho \frac{L}{R}
\]
Thay các giá trị vào:
\[
A = 2.82 \times 10^{-8} \times \frac{50}{5} = 2.82 \times 10^{-8} \times 10 = 2.82 \times 10^{-7}\, \text{m}^2
\]
Vậy tiết diện ngang tối thiểu của dây dẫn cần là \(2.82 \times 10^{-7}\, \text{m}^2\) để đảm bảo điện trở không vượt quá \(5\, \Omega\).