Chủ đề từ trường đều: Từ trường đều là một khái niệm quan trọng trong vật lý học, mang lại nhiều ứng dụng thực tiễn trong đời sống và công nghệ. Bài viết này sẽ khám phá chi tiết về cách tạo ra từ trường đều, đặc điểm của nó, và những ứng dụng nổi bật giúp nâng cao hiểu biết của bạn về thế giới tự nhiên.
Mục lục
Tìm Hiểu Về Từ Trường Đều
Từ trường đều là một khái niệm quan trọng trong vật lý học, liên quan đến các hiện tượng từ tính và lực từ tác động lên các đối tượng. Dưới đây là thông tin chi tiết về khái niệm, đặc điểm, và ứng dụng của từ trường đều.
1. Khái Niệm Từ Trường Đều
Từ trường đều là một loại từ trường trong đó các đường sức từ là những đường thẳng song song và cách đều nhau. Điều này có nghĩa là cảm ứng từ tại mọi điểm trong từ trường đều có độ lớn và hướng như nhau. Độ lớn của từ trường đều ký hiệu là \(B\) và được biểu diễn bằng công thức:
\[ B = \text{const} \]
2. Đặc Điểm Của Từ Trường Đều
- Đường sức từ song song và cách đều: Các đường sức từ trong từ trường đều là các đường thẳng song song và khoảng cách giữa chúng không thay đổi.
- Độ lớn cảm ứng từ không đổi: Cảm ứng từ tại mọi điểm trong từ trường đều có giá trị như nhau.
- Ứng dụng trong lý thuyết và thực tế: Từ trường đều thường được sử dụng trong nghiên cứu lý thuyết cũng như trong các ứng dụng thực tế như các thiết bị điện từ.
3. Cách Tạo Ra Từ Trường Đều
Từ trường đều có thể được tạo ra bằng một số phương pháp cụ thể:
- Nam châm chữ U: Sử dụng nam châm chữ U, khoảng không gian giữa hai cực của nam châm tạo ra một từ trường đều với các đường sức từ song song.
- Ống dây dẫn có dòng điện: Khi cho dòng điện chạy qua một ống dây dẫn, một từ trường đều được tạo ra bên trong lòng ống dây do các đường sức từ bên trong song song và cách đều nhau.
- Hệ thống dây dẫn thẳng dài: Sắp xếp nhiều dây dẫn thẳng dài song song và cách đều nhau để tạo ra một vùng không gian có từ trường đều.
4. Công Thức Tính Toán Trong Từ Trường Đều
| Công Thức | Mô Tả |
|---|---|
| \( F = B \cdot I \cdot L \cdot \sin(\theta) \) | Lực từ tác động lên một dây dẫn có dòng điện nằm trong từ trường đều. |
| \( B = \frac{F}{I \cdot L \cdot \sin(\theta)} \) | Tính cảm ứng từ tại một điểm trong từ trường đều. |
5. Ứng Dụng Thực Tiễn Của Từ Trường Đều
- Kiểm tra chất lượng vật liệu: Sử dụng từ trường đều để phát hiện khuyết tật bên trong kim loại bằng kỹ thuật kiểm tra không phá hủy (NDT).
- Hệ thống tàu đệm từ (maglev): Từ trường đều được sử dụng để nâng và di chuyển tàu mà không cần tiếp xúc với đường ray, giúp giảm ma sát và tăng tốc độ.
- Thiết bị điện tử và máy móc: Từ trường đều được ứng dụng trong các thiết bị điện tử và cơ khí như máy phát điện, động cơ điện và các hệ thống điều khiển từ xa.
6. Kết Luận
Từ trường đều là một khái niệm cơ bản trong vật lý học với nhiều ứng dụng quan trọng trong khoa học và kỹ thuật. Việc hiểu rõ đặc điểm và cách tạo ra từ trường đều giúp nâng cao hiệu quả trong nghiên cứu và ứng dụng thực tế, mở ra nhiều cơ hội phát triển mới trong các lĩnh vực khoa học và kỹ thuật.

.png)
1. Định Nghĩa Từ Trường Đều
Từ trường đều là một loại từ trường trong đó các đường sức từ là những đường thẳng song song và cách đều nhau. Điều này có nghĩa là cảm ứng từ tại mọi điểm trong từ trường đều có độ lớn và hướng như nhau. Trong vật lý, từ trường đều thường được sử dụng để đơn giản hóa các bài toán và nghiên cứu.
Ví dụ, từ trường đều có thể được tạo ra giữa hai cực của nam châm hình chữ U hoặc bên trong lòng một ống dây dẫn có dòng điện. Khi dòng điện chạy qua ống dây dẫn, từ trường đều xuất hiện do các đường sức từ bên trong ống dây song song và cách đều nhau. Độ lớn của từ trường đều bên trong ống dây được tính theo công thức:
- \(B\): Độ lớn của từ trường đều
- \(\mu_0\): Độ thẩm từ của chân không
- \(n\): Số vòng dây trên một đơn vị chiều dài
- \(I\): Cường độ dòng điện chạy qua ống dây
- \(l\): Chiều dài của ống dây
Từ trường đều có nhiều đặc tính quan trọng, chẳng hạn như:
- Các đường sức từ song song, cùng chiều và cách đều nhau.
- Cảm ứng từ tại mọi điểm trong từ trường đều bằng nhau.
- Lực từ tác động lên các đối tượng trong từ trường đều là đồng nhất, không thay đổi theo vị trí.
Các đặc tính này khiến từ trường đều trở thành một công cụ quan trọng trong nghiên cứu và ứng dụng, đặc biệt là trong các lĩnh vực như vật lý, điện tử, và công nghệ thông tin. Từ trường đều được sử dụng trong các thiết bị từ tính, các thí nghiệm khoa học, và trong lý thuyết điện từ học để mô hình hóa các hiện tượng phức tạp một cách dễ hiểu hơn.
2. Cách Tạo Ra Từ Trường Đều
Để tạo ra từ trường đều, cần thiết lập một không gian trong đó các đường sức từ song song, cùng chiều và cách đều nhau. Dưới đây là một số phương pháp phổ biến để tạo ra từ trường đều:
- Sử dụng nam châm chữ U: Một trong những cách đơn giản nhất để tạo từ trường đều là sử dụng nam châm chữ U. Không gian giữa hai cực của nam châm chữ U có thể tạo ra một từ trường đều vì các đường sức từ ở đó song song và cách đều nhau.
- Ống dây dẫn có dòng điện: Khi dòng điện chạy qua một ống dây dẫn, từ trường được tạo ra bên trong lòng ống dây sẽ là từ trường đều. Điều này là do các đường sức từ trong ống dây sẽ song song và cách đều nhau.
- Giả sử có một ống dây với \(n\) vòng dây và dòng điện \(I\) chạy qua.
- Từ trường đều bên trong ống dây có thể tính bằng công thức: \(B = \mu_0 \cdot \frac{nI}{l}\), trong đó \(\mu_0\) là hằng số từ trường trong chân không, \(n\) là số vòng dây, \(I\) là cường độ dòng điện, và \(l\) là chiều dài của ống dây.
- Dòng điện chạy qua dây dẫn thẳng dài: Khi có nhiều dây dẫn thẳng dài song song và dòng điện chạy qua chúng cùng chiều, các từ trường xung quanh dây dẫn sẽ cộng hưởng và tạo thành một vùng không gian với từ trường đều.
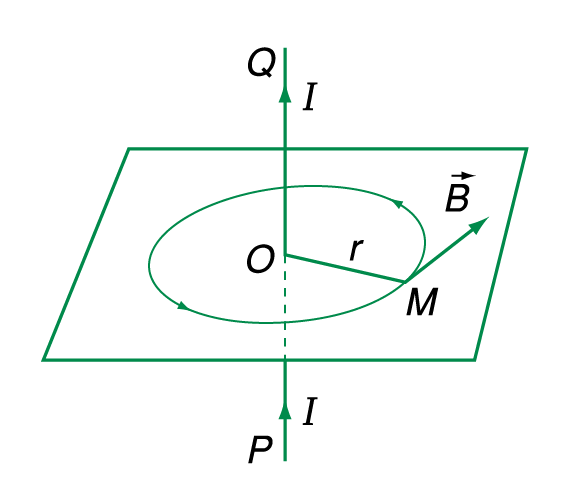
- Cảm ứng từ tại một điểm cách dây dẫn một khoảng \(r\) được tính bằng: \[B = \frac{\mu_0 I}{2\pi r}\]
- Nếu có nhiều dây dẫn song song, từ trường tại một vùng không gian giữa các dây sẽ là từ trường đều do sự cộng hưởng của các từ trường tạo ra từ mỗi dây.
Những phương pháp này giúp chúng ta tạo ra từ trường đều cho các ứng dụng khoa học và kỹ thuật, từ việc kiểm tra chất lượng vật liệu đến việc phát triển hệ thống giao thông hiện đại như tàu đệm từ.

3. Công Thức và Phương Pháp Tính Toán
Việc tính toán trong từ trường đều giúp hiểu rõ hơn về lực từ, cảm ứng từ và các yếu tố ảnh hưởng đến chúng. Dưới đây là các công thức cơ bản và phương pháp tính toán thường được sử dụng trong các bài toán liên quan đến từ trường đều:
- Công thức tính cảm ứng từ: Trong từ trường đều, cảm ứng từ \(B\) có thể được tính bằng công thức:
\[
B = \frac{F}{I \cdot L \cdot \sin(\theta)}
\]
Trong đó:
- \(F\) là lực từ tác động lên dây dẫn (đơn vị: Newton, N)
- \(I\) là cường độ dòng điện chạy qua dây dẫn (đơn vị: Ampere, A)
- \(L\) là chiều dài của dây dẫn nằm trong từ trường (đơn vị: mét, m)
- \(\theta\) là góc giữa dòng điện và hướng của từ trường (đơn vị: độ hoặc radian)
- Tính lực từ trên dây dẫn: Lực từ \(F\) tác động lên một dây dẫn có dòng điện chạy qua trong từ trường đều có thể được tính bằng công thức: \[ F = B \cdot I \cdot L \cdot \sin(\theta) \] Đây là lực Lorentz, biểu diễn sự tương tác giữa dòng điện và từ trường.
- Công thức tính từ thông: Từ thông \(\Phi\) qua một diện tích \(A\) trong từ trường đều được tính bằng:
\[
\Phi = B \cdot A \cdot \cos(\alpha)
\]
Trong đó:
- \(B\) là độ lớn của cảm ứng từ (đơn vị: Tesla, T)
- \(A\) là diện tích bề mặt vuông góc với từ trường (đơn vị: mét vuông, m²)
- \(\alpha\) là góc giữa vectơ cảm ứng từ và vectơ pháp tuyến của diện tích \(A\)
Để tính toán chính xác trong các bài toán về từ trường đều, cần tuân thủ các bước sau:
- Xác định các yếu tố đã biết: dòng điện \(I\), chiều dài dây dẫn \(L\), góc \(\theta\), độ lớn cảm ứng từ \(B\).
- Chọn công thức phù hợp với bài toán: nếu cần tính lực từ, sử dụng công thức lực Lorentz; nếu cần tính cảm ứng từ, sử dụng công thức cảm ứng từ; nếu tính từ thông, sử dụng công thức từ thông.
- Thay giá trị đã biết vào công thức và thực hiện phép tính để tìm giá trị cần tìm.
Hiểu rõ và áp dụng các công thức này sẽ giúp bạn nắm vững kiến thức về từ trường đều và áp dụng chúng vào các ứng dụng thực tế một cách hiệu quả.

4. Ứng Dụng Của Từ Trường Đều
Từ trường đều có nhiều ứng dụng quan trọng trong khoa học, y học, công nghệ điện tử, và công nghiệp. Sự đồng nhất của từ trường đều giúp tối ưu hóa các quá trình kiểm tra và nâng cao hiệu suất trong các ứng dụng khác nhau. Dưới đây là một số ứng dụng nổi bật của từ trường đều:
- Trong y học:
Từ trường đều được sử dụng trong thiết bị chụp cộng hưởng từ (MRI), cho phép tạo ra hình ảnh chi tiết của các mô mềm trong cơ thể. Nhờ vào sự phản ứng khác nhau của các mô với từ trường, MRI cung cấp khả năng chẩn đoán chính xác mà không cần can thiệp phẫu thuật.
- Trong công nghệ điện tử:
Các linh kiện điện tử như loa, micro và tai nghe sử dụng từ trường đều để chuyển đổi tín hiệu điện thành âm thanh và ngược lại. Nguyên lý cảm ứng từ giúp các thiết bị này hoạt động hiệu quả và tạo ra chất lượng âm thanh tốt hơn.
- Trong công nghiệp:
Từ trường đều được ứng dụng trong kỹ thuật kiểm tra không phá hủy (NDT) để kiểm tra chất lượng vật liệu và phát hiện các khuyết tật bên trong kim loại mà không cần phá hủy mẫu vật. Phương pháp này giúp đảm bảo chất lượng và an toàn trong sản xuất công nghiệp.
- Trong giao thông:
Hệ thống tàu đệm từ (maglev) sử dụng từ trường đều để nâng và di chuyển tàu mà không cần tiếp xúc với đường ray. Điều này giúp giảm ma sát, tiết kiệm năng lượng và tăng tốc độ di chuyển, mở ra tương lai của giao thông công cộng nhanh và hiệu quả hơn.
Những ứng dụng của từ trường đều không chỉ giúp cải thiện các công nghệ hiện có mà còn mở ra cơ hội phát triển mới trong nhiều lĩnh vực khác nhau, từ y học đến công nghiệp và giao thông.

5. Tầm Quan Trọng Của Từ Trường Đều Trong Vật Lý và Kỹ Thuật
Từ trường đều đóng một vai trò quan trọng trong nhiều lĩnh vực vật lý và kỹ thuật, nhờ vào khả năng tạo ra một môi trường từ trường ổn định và đồng đều. Điều này giúp cải thiện độ chính xác trong các phép đo và phân tích, đặc biệt là trong nghiên cứu và phát triển công nghệ. Dưới đây là một số lý do cụ thể làm nổi bật tầm quan trọng của từ trường đều:
- Trong Vật Lý:
Từ trường đều cung cấp một môi trường đồng nhất, giúp dễ dàng nghiên cứu các đặc tính từ tính của vật liệu. Điều này rất hữu ích trong các thí nghiệm vật lý cần kiểm soát các yếu tố khác để tập trung vào tác động của từ trường.
Ví dụ, trong các thí nghiệm đo lường lực từ, từ trường đều giúp đảm bảo kết quả đo chính xác hơn do từ trường không thay đổi tại các điểm khác nhau trong vùng nghiên cứu.
- Trong Kỹ Thuật:
Trong công nghệ điện, từ trường đều được ứng dụng rộng rãi trong các thiết bị như máy biến áp, máy phát điện và thiết bị bảo vệ hệ thống điện. Từ trường đều giúp các thiết bị này hoạt động ổn định và hiệu quả.
Trong kỹ thuật y sinh, từ trường đều đóng vai trò quan trọng trong các phương pháp hình ảnh y học như MRI (cộng hưởng từ hạt nhân), nơi cần một từ trường mạnh và ổn định để tạo ra hình ảnh rõ nét và chính xác của cơ thể người.
- Trong Công Nghiệp:
Từ trường đều được sử dụng để kiểm tra và phân tích vật liệu, giúp xác định cấu trúc và tính chất từ của các chất liệu khác nhau. Điều này đặc biệt hữu ích trong các quy trình sản xuất yêu cầu chất lượng cao và kiểm soát chặt chẽ.
Ngoài ra, trong công nghệ chế tạo, từ trường đều có thể được sử dụng để điều khiển các hạt từ tính trong các ứng dụng sản xuất và gia công chính xác.
Tóm lại, từ trường đều không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tiễn trong nhiều lĩnh vực khác nhau. Nó giúp tăng độ chính xác, hiệu quả và an toàn trong các ứng dụng vật lý và kỹ thuật, từ đó đóng góp lớn vào sự phát triển khoa học và công nghệ.
XEM THÊM:
6. Ví Dụ và Bài Tập Minh Họa
Dưới đây là một số ví dụ và bài tập minh họa về từ trường đều, giúp bạn nắm vững các khái niệm và phương pháp tính toán liên quan.
6.1. Tính lực từ tác dụng lên dây dẫn
Giả sử chúng ta có một dây dẫn thẳng dài l đặt trong từ trường đều B, vuông góc với chiều dòng điện I. Lực từ F tác dụng lên dây dẫn này được tính theo công thức:
\[
F = I \cdot l \cdot B \cdot \sin(\theta)
\]
Trong đó:
- I: Cường độ dòng điện chạy qua dây dẫn (đơn vị: A)
- l: Chiều dài của dây dẫn trong từ trường (đơn vị: m)
- B: Độ lớn cảm ứng từ của từ trường (đơn vị: T)
- \(\theta\): Góc giữa dây dẫn và đường sức từ (đơn vị: độ)
Ví dụ: Một dây dẫn dài 1.5m, mang dòng điện 10A, đặt trong từ trường đều 0.5T và vuông góc với từ trường. Hãy tính lực từ tác dụng lên dây dẫn.
Áp dụng công thức:
\[
F = 10 \times 1.5 \times 0.5 \times \sin(90^\circ) = 7.5 \, \text{N}
\]
6.2. Bài tập áp dụng công thức từ trường đều
Bài tập 1: Một khung dây dẫn hình vuông có cạnh dài 0.4m, nằm trong một từ trường đều có cảm ứng từ B = 0.3T. Cho dòng điện I = 5A chạy qua khung dây. Xác định lực từ tác dụng lên mỗi cạnh của khung dây.
Ta biết rằng lực từ tác dụng lên mỗi cạnh của khung dây được tính bằng công thức:
\[
F = I \cdot l \cdot B
\]
Trong trường hợp này, chiều dài cạnh l = 0.4m, dòng điện I = 5A, và cảm ứng từ B = 0.3T.
Áp dụng công thức:
\[
F = 5 \times 0.4 \times 0.3 = 0.6 \, \text{N}
\]
Vậy lực từ tác dụng lên mỗi cạnh của khung dây là 0.6N.
6.3. Bài tập tính toán cảm ứng từ
Bài tập 2: Một dây dẫn thẳng dài mang dòng điện I = 8A được đặt trong từ trường đều có cảm ứng từ B = 0.2T. Nếu dây dẫn tạo với từ trường một góc 30°, hãy tính độ lớn lực từ tác dụng lên dây dẫn.
Áp dụng công thức tính lực từ:
\[
F = I \cdot l \cdot B \cdot \sin(\theta)
\]
Với \(\theta = 30^\circ\), chúng ta có:
\[
F = 8 \times l \times 0.2 \times \sin(30^\circ) = 8 \times l \times 0.2 \times 0.5 = 0.8 \times l \, \text{N}
\]
Vậy lực từ tác dụng lên dây dẫn là 0.8l Newton.
Những bài tập này giúp củng cố kiến thức về từ trường đều và các ứng dụng thực tế trong việc tính toán lực từ và cảm ứng từ trong các hệ thống vật lý khác nhau.