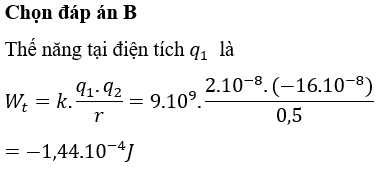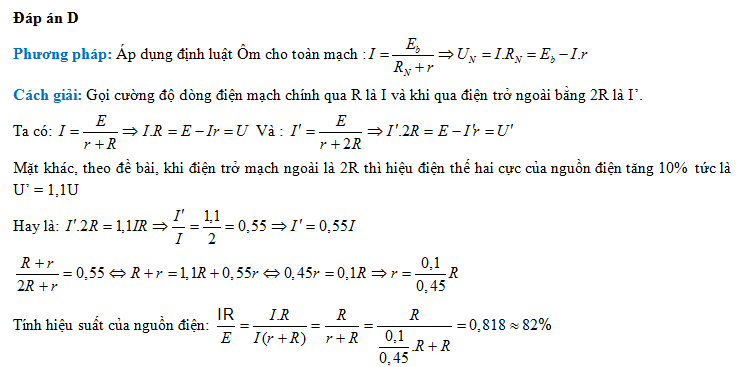Chủ đề thế năng điện kết nối tri thức: Thế năng điện là một khái niệm quan trọng trong vật lý, giúp học sinh hiểu rõ hơn về công và thế năng của điện tích trong điện trường. Bài viết này sẽ cung cấp kiến thức cơ bản, lý thuyết quan trọng cùng các bài tập minh họa chi tiết, giúp bạn nắm vững và áp dụng hiệu quả trong học tập. Cùng khám phá ngay để tăng cường hiểu biết của bạn về thế năng điện!
Mục lục
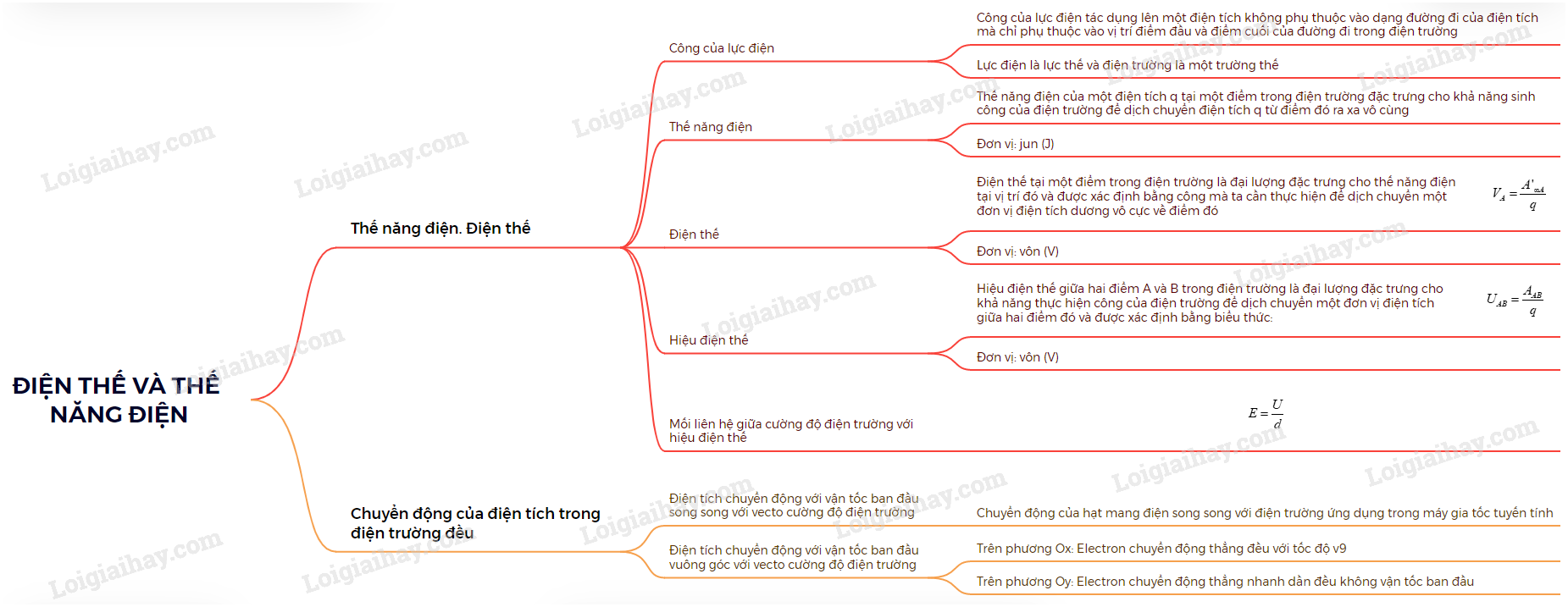
Thế Năng Điện - Kết Nối Tri Thức
Thế năng điện là một phần quan trọng trong chương trình Vật lý lớp 11 theo bộ sách giáo khoa "Kết nối tri thức". Chủ đề này giúp học sinh hiểu rõ về khái niệm thế năng trong điện trường và cách tính toán liên quan.
Định nghĩa và ý nghĩa
Thế năng điện là năng lượng mà một điện tích có được do vị trí của nó trong một điện trường. Khái niệm này giúp học sinh hiểu về lực điện và công của lực điện khi dịch chuyển điện tích trong điện trường.
Các công thức quan trọng
- Công thức tổng quát: \( W = q \cdot V \)
- Công thức tính công của lực điện: \( A = q \cdot E \cdot d \)
Bài tập thực hành
Trong chương trình học, học sinh sẽ được làm quen với các dạng bài tập khác nhau như nhận biết, thông hiểu và vận dụng. Các bài tập này thường xoay quanh việc tính toán thế năng, công của lực điện và cách áp dụng vào các bài toán thực tế.
Ứng dụng trong thực tế
Thế năng điện không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng trong cuộc sống hàng ngày, như trong thiết kế mạch điện, động cơ điện và các thiết bị điện tử.
Kết luận
Việc hiểu và nắm vững khái niệm thế năng điện giúp học sinh phát triển tư duy logic và khả năng giải quyết vấn đề trong các bài toán vật lý. Chủ đề này không chỉ giúp cải thiện kiến thức học thuật mà còn mở rộng hiểu biết về thế giới xung quanh.
.png)
Lý thuyết cơ bản về thế năng điện
Thế năng điện là một khái niệm quan trọng trong vật lý, thể hiện khả năng sinh công của điện trường khi đặt một điện tích tại một vị trí nhất định trong trường đó. Để hiểu rõ hơn, ta cần đi qua các khái niệm cơ bản như sau:
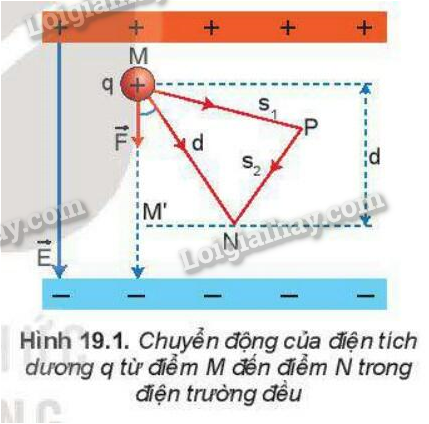
- 1. Công của lực điện: Khi điện tích q di chuyển trong một điện trường đều từ điểm M đến điểm N, công của lực điện trường lên điện tích này được tính bằng công thức \(A_{MN} = qEd\), trong đó d là độ dịch chuyển của điện tích theo phương của lực điện.
- 2. Thế năng của điện tích: Thế năng của một điện tích q tại một điểm trong điện trường là đại lượng đặc trưng cho khả năng sinh công của điện trường khi điện tích di chuyển từ vị trí đó đến một điểm khác. Công thức tính thế năng điện là \(W = qV\), trong đó V là điện thế tại điểm đang xét.
- 3. Sự khác biệt giữa thế năng điện và công: Trong khi công của lực điện phụ thuộc vào quãng đường dịch chuyển của điện tích, thế năng điện chỉ phụ thuộc vào vị trí của điện tích trong điện trường.
Bằng cách nắm vững các khái niệm trên, học sinh có thể hiểu rõ hơn về các hiện tượng điện học và ứng dụng của thế năng điện trong thực tế.
Các dạng bài tập và ví dụ minh họa
Trong quá trình học tập và nghiên cứu về thế năng điện, các dạng bài tập và ví dụ minh họa đóng vai trò rất quan trọng trong việc giúp học sinh nắm vững lý thuyết và áp dụng vào thực tế. Dưới đây là một số dạng bài tập cơ bản và ví dụ minh họa giúp bạn hiểu rõ hơn về chủ đề này.
-
Dạng 1: Tính công của lực điện trong điện trường đều
Cho một điện tích q di chuyển trong điện trường đều có cường độ điện trường E. Bài toán yêu cầu tính công của lực điện khi điện tích di chuyển từ điểm A đến điểm B.
Ví dụ: Một điện tích q = 5x10-6 C di chuyển trong điện trường đều E = 1000 V/m trên một đoạn đường d = 2 m. Tính công của lực điện.
Hướng dẫn giải: Công của lực điện được tính bằng công thức:
$$ A = qEd $$
Thay số vào công thức, ta có:
$$ A = 5x10^{-6} * 1000 * 2 = 0.01 J $$
Vậy công của lực điện là 0.01 J.
-
Dạng 2: Tính thế năng của một điện tích trong điện trường
Bài toán yêu cầu tính thế năng của một điện tích q tại một điểm trong điện trường, dựa trên vị trí và cường độ của điện trường.
Ví dụ: Một điện tích q = 2x10-6 C được đặt tại một điểm cách bản cực âm của một tụ điện phẳng một khoảng 1 m trong điện trường đều E = 500 V/m. Tính thế năng của điện tích tại điểm đó.
Hướng dẫn giải: Thế năng của điện tích được tính bằng công thức:
$$ W = qEd $$
Thay số vào công thức, ta có:
$$ W = 2x10^{-6} * 500 * 1 = 0.001 J $$
Vậy thế năng của điện tích tại điểm đó là 0.001 J.
-
Dạng 3: Tính công của lực điện trong điện trường không đều
Trong trường hợp này, bài toán yêu cầu tính công của lực điện khi điện tích di chuyển từ một điểm này đến một điểm khác trong điện trường không đều.
Ví dụ: Một điện tích q di chuyển từ điểm A đến điểm B trong một điện trường không đều. Tại A, điện trường có cường độ EA = 200 V/m, tại B, EB = 300 V/m. Đoạn đường đi dài 1.5 m. Tính công của lực điện.
Hướng dẫn giải: Công của lực điện trong điện trường không đều tính bằng cách tích phân lực điện trên quãng đường di chuyển:
$$ A = \int_{A}^{B} \vec{F} \cdot d\vec{s} $$
Ở đây, cần xác định chính xác lực điện tại từng điểm trên đường đi để tính công.
Những dạng bài tập và ví dụ trên giúp bạn hiểu rõ hơn về cách áp dụng lý thuyết thế năng điện vào giải quyết các bài toán thực tế. Qua việc thực hành các bài tập này, bạn sẽ nắm vững hơn kiến thức về thế năng điện và khả năng áp dụng vào các bài toán phức tạp hơn.

Ứng dụng và thực hành
Trong thực tế, việc ứng dụng thế năng điện không chỉ giới hạn trong các bài toán lý thuyết mà còn có rất nhiều ứng dụng thực tiễn. Dưới đây là một số ví dụ và bài tập minh họa giúp bạn hiểu rõ hơn về cách áp dụng kiến thức này.
1. Ứng dụng trong tính toán công của lực điện
- Ví dụ 1: Xác định công của lực điện khi một điện tích q di chuyển từ điểm A đến điểm B trong điện trường đều.
- Bài tập: Cho một điện tích q = 2C, di chuyển trong điện trường đều có \( E = 5N/C \), khoảng cách d = 10m. Tính công của lực điện.
Lời giải: Sử dụng công thức \( W = qEd \), trong đó \(E\) là cường độ điện trường và \(d\) là khoảng cách giữa hai điểm.
Đáp án: Áp dụng công thức \( W = qEd = 2 * 5 * 10 = 100J \).
2. Ứng dụng trong xác định thế năng điện
- Ví dụ 2: Xác định thế năng điện của một điện tích q tại một điểm trong điện trường.
- Bài tập: Cho điện tích q = 3C, đặt tại điểm có điện thế V = 12V. Tính thế năng điện.
Lời giải: Sử dụng công thức \( W = qV \), trong đó V là điện thế tại điểm đó.
Đáp án: Áp dụng công thức \( W = qV = 3 * 12 = 36J \).
3. Ứng dụng trong tính toán hiệu suất của hệ thống
- Ví dụ 3: Xác định hiệu suất chuyển đổi năng lượng từ thế năng điện sang năng lượng khác.
- Bài tập: Một hệ thống có công toàn phần là 200J, công có ích là 150J. Tính hiệu suất.
Lời giải: Sử dụng công thức hiệu suất \( \eta = \frac{\text{Công có ích}}{\text{Công toàn phần}} \times 100\% \).
Đáp án: \( \eta = \frac{150}{200} \times 100\% = 75\% \).
4. Thực hành và thí nghiệm
- Thí nghiệm: Thực hiện thí nghiệm đo điện thế giữa hai điểm trong một điện trường đều bằng cách sử dụng các thiết bị đo điện thế.
Gợi ý: Sử dụng các dụng cụ đo hiện đại để kiểm tra và so sánh kết quả thực tế với lý thuyết.
5. Thực hành trong đời sống
- Ứng dụng thực tế: Sử dụng kiến thức về thế năng điện trong việc thiết kế hệ thống điện mặt trời, nơi điện thế được tạo ra và lưu trữ cho các mục đích sử dụng sau này.