Sau 2 Giờ Độ Phóng Xạ Giảm 4 Lần - Giải Thích Hiện Tượng Và Ứng Dụng Thực Tế

Khi tìm kiếm với từ khóa "sau 2 giờ độ phóng xạ giảm 4 lần," nhiều bài viết và tài liệu học tập trên các trang web giáo dục đã cung cấp thông tin chi tiết về hiện tượng này. Dưới đây là tổng hợp các kiến thức liên quan:

1. Hiện tượng giảm độ phóng xạ

Hiện tượng giảm độ phóng xạ của một chất sau một khoảng thời gian nhất định liên quan đến chu kỳ bán rã của chất đó. Chu kỳ bán rã là thời gian cần thiết để một nửa lượng chất phóng xạ ban đầu phân rã. Trong trường hợp này, sau 2 giờ, độ phóng xạ của một mẫu chất giảm 4 lần, điều này cho thấy chất phóng xạ đã trải qua hai chu kỳ bán rã trong thời gian này.

2. Công thức tính toán

Để hiểu rõ hơn về sự giảm độ phóng xạ, ta có thể sử dụng công thức liên quan đến chu kỳ bán rã:

\[ H(t) = H_0 \times 2^{-\frac{t}{T}} \]

Trong đó:

• H(t): Độ phóng xạ tại thời điểm t
• H_0: Độ phóng xạ ban đầu
• T: Chu kỳ bán rã

Nếu sau 2 giờ, độ phóng xạ giảm 4 lần, ta có:

\[ \frac{H_0}{4} = H_0 \times 2^{-\frac{2}{T}} \]

Từ đó suy ra, chu kỳ bán rã của chất phóng xạ này là 1 giờ:

\[ T = 1 \text{ giờ} \]

3. Các bài tập liên quan

Nhiều trang web cung cấp các bài tập về tính toán chu kỳ bán rã dựa trên các dữ kiện tương tự. Những bài tập này giúp người học củng cố kiến thức về vật lý hạt nhân, cụ thể là về phóng xạ và chu kỳ bán rã.

4. Ứng dụng thực tế

Hiểu biết về chu kỳ bán rã và sự giảm độ phóng xạ là cơ sở quan trọng trong các lĩnh vực như y học hạt nhân, xử lý chất thải phóng xạ, và các nghiên cứu khoa học liên quan đến phóng xạ.

Tổng hợp lại, kiến thức về sự giảm độ phóng xạ và chu kỳ bán rã không chỉ quan trọng trong lý thuyết mà còn có nhiều ứng dụng thực tế trong đời sống.

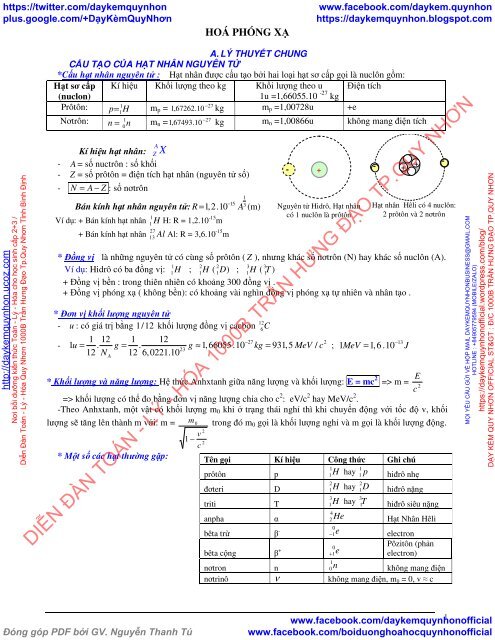
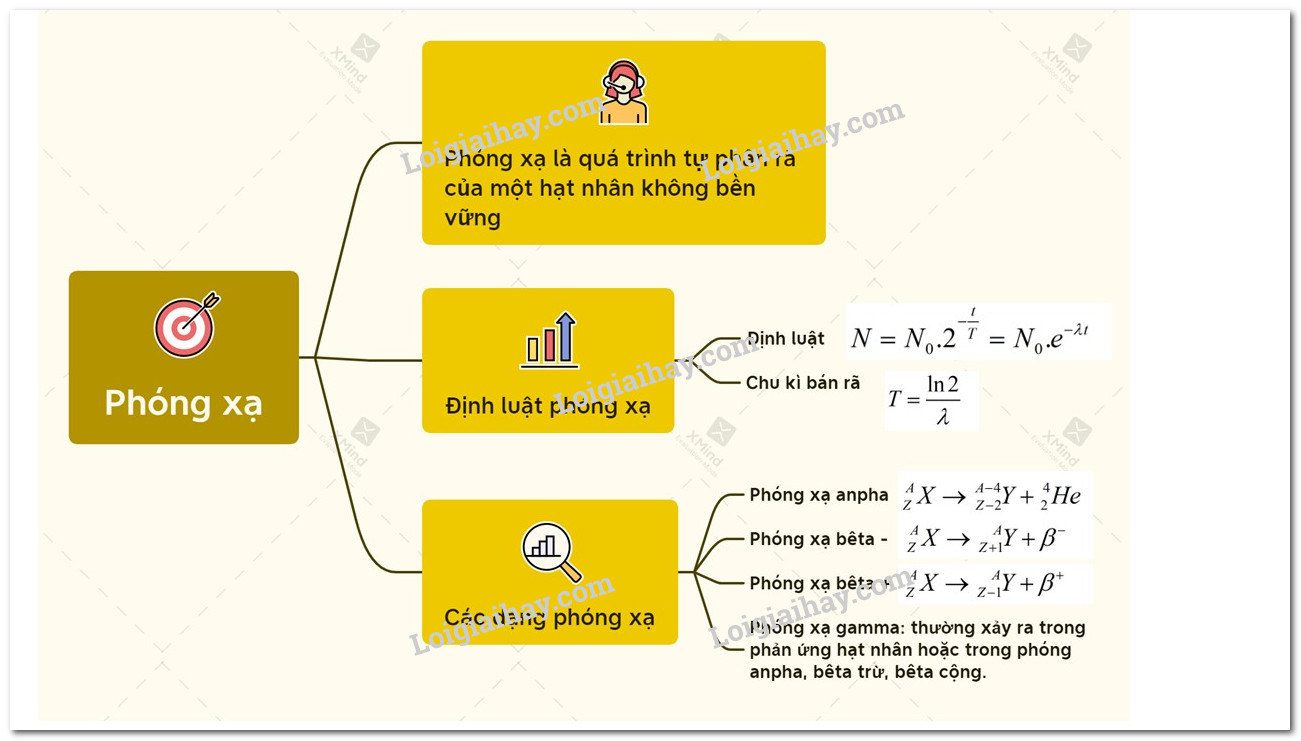
Độ phóng xạ là hiện tượng một hạt nhân không bền tự phát phân rã và phát ra bức xạ ion hóa, gồm có tia alpha, beta, hoặc gamma. Mỗi chất phóng xạ có một chu kỳ bán rã nhất định, đây là khoảng thời gian để một nửa lượng chất phóng xạ ban đầu bị phân rã.

Chu kỳ bán rã có thể được biểu diễn bằng phương trình:

Trong đó:

• \(N(t)\): Số lượng hạt nhân còn lại sau thời gian \(t\)
• \(N_0\): Số lượng hạt nhân ban đầu
• \(\lambda\): Hằng số phân rã

Chu kỳ bán rã \(T\) liên hệ với hằng số phân rã qua công thức:

Ví dụ, nếu độ phóng xạ của một chất giảm đi 4 lần sau 2 giờ, thì chu kỳ bán rã của chất đó sẽ là 1 giờ. Điều này có nghĩa là sau mỗi 1 giờ, lượng chất phóng xạ sẽ giảm đi một nửa.

Công thức tính độ phóng xạ sau thời gian \(t\) với chu kỳ bán rã \(T\) được biểu diễn như sau:

Áp dụng công thức này, nếu sau 2 giờ độ phóng xạ giảm 4 lần, chúng ta có thể suy ra chu kỳ bán rã của chất là 1 giờ.

Việc hiểu rõ về độ phóng xạ và chu kỳ bán rã không chỉ quan trọng trong nghiên cứu khoa học mà còn trong các ứng dụng thực tiễn như y học hạt nhân, bảo vệ môi trường, và quản lý chất thải phóng xạ.

Quá trình phân rã phóng xạ tuân theo định luật phân rã theo hàm mũ, trong đó độ phóng xạ của một chất giảm dần theo thời gian. Giả sử độ phóng xạ ban đầu của chất phóng xạ là \(A_0\) và độ phóng xạ sau một khoảng thời gian \(t\) là \(A(t)\), ta có phương trình:

Trong đó:

• \(A(t)\): Độ phóng xạ tại thời điểm \(t\)
• \(A_0\): Độ phóng xạ ban đầu
• \(\lambda\): Hằng số phân rã phóng xạ, đặc trưng cho chất phóng xạ
• \(t\): Thời gian

Theo đề bài, sau 2 giờ độ phóng xạ giảm 4 lần, điều này có nghĩa là:

Thay giá trị vào phương trình phân rã:

Chia cả hai vế cho \(A_0\):

Lấy logarit tự nhiên của hai vế:

Do \(\ln\left(\frac{1}{4}\right) = -\ln(4)\), ta có:

Suy ra hằng số phân rã \(\lambda\):

Với giá trị của \(\lambda\) này, ta có thể tính toán độ phóng xạ tại bất kỳ thời điểm nào bằng cách sử dụng công thức:

Điều này có nghĩa là độ phóng xạ của chất phóng xạ sẽ tiếp tục giảm dần theo thời gian, với tốc độ giảm phụ thuộc vào hằng số phân rã \(\lambda\). Để hiểu rõ hơn quá trình này, chúng ta có thể sử dụng đồ thị của hàm số mũ để hình dung sự giảm dần của độ phóng xạ theo thời gian.

Dưới đây là một số bài tập minh họa về chu kỳ bán rã, dựa trên khái niệm độ phóng xạ giảm dần theo thời gian.

1. Bài tập 1: Một mẫu phóng xạ có chu kỳ bán rã là 2 giờ. Sau 2 giờ, độ phóng xạ của nó giảm đi 4 lần. Tính chu kỳ bán rã của mẫu phóng xạ này.

   Lời giải:

   • Giả sử ban đầu mẫu phóng xạ có độ phóng xạ là \(R_0\). Sau thời gian \(t = 2\) giờ, độ phóng xạ giảm đi 4 lần, tức là \(R = \frac{R_0}{4}\).
   • Áp dụng công thức tính độ phóng xạ theo thời gian: \[ R = R_0 \cdot \left( \frac{1}{2} \right)^{\frac{t}{T_{1/2}}} \] Trong đó:
     • \(R\) là độ phóng xạ còn lại sau thời gian \(t\).
     • \(T_{1/2}\) là chu kỳ bán rã của chất phóng xạ.
   • Thay các giá trị vào công thức: \[ \frac{R_0}{4} = R_0 \cdot \left( \frac{1}{2} \right)^{\frac{2}{T_{1/2}}} \] Rút gọn \(R_0\): \[ \frac{1}{4} = \left( \frac{1}{2} \right)^{\frac{2}{T_{1/2}}} \] Giải phương trình: \[ \frac{2}{T_{1/2}} = 2 \Rightarrow T_{1/2} = 1 \text{ giờ.} \]

   Vậy chu kỳ bán rã của mẫu phóng xạ là 1 giờ.

2. Bài tập 2: Một chất phóng xạ có chu kỳ bán rã là 5 giờ. Tính độ phóng xạ còn lại sau 10 giờ nếu ban đầu độ phóng xạ là \(R_0\).

   Lời giải:

   • Áp dụng công thức tính độ phóng xạ theo thời gian: \[ R = R_0 \cdot \left( \frac{1}{2} \right)^{\frac{t}{T_{1/2}}} \]
   • Thay các giá trị \(t = 10\) giờ và \(T_{1/2} = 5\) giờ vào công thức: \[ R = R_0 \cdot \left( \frac{1}{2} \right)^{\frac{10}{5}} = R_0 \cdot \left( \frac{1}{2} \right)^2 = R_0 \cdot \frac{1}{4} \]
   • Vậy độ phóng xạ còn lại sau 10 giờ là \(R = \frac{R_0}{4}\).

3. Bài tập 3: Một mẫu phóng xạ có chu kỳ bán rã là 3 giờ. Nếu ban đầu mẫu có 200 nguyên tử phóng xạ, hỏi sau 9 giờ còn bao nhiêu nguyên tử phóng xạ chưa phân rã?

   Lời giải:

   • Số nguyên tử phóng xạ còn lại được tính bằng công thức: \[ N = N_0 \cdot \left( \frac{1}{2} \right)^{\frac{t}{T_{1/2}}} \] Trong đó:
     • \(N\) là số nguyên tử còn lại sau thời gian \(t\).
     • \(N_0\) là số nguyên tử ban đầu.
   • Thay các giá trị \(t = 9\) giờ và \(T_{1/2} = 3\) giờ vào công thức: \[ N = 200 \cdot \left( \frac{1}{2} \right)^{\frac{9}{3}} = 200 \cdot \left( \frac{1}{2} \right)^3 = 200 \cdot \frac{1}{8} = 25 \text{ nguyên tử.} \]
   • Vậy sau 9 giờ, còn lại 25 nguyên tử phóng xạ chưa phân rã.

Kiến thức về độ phóng xạ và chu kỳ bán rã không chỉ là lý thuyết mà còn có nhiều ứng dụng thực tế trong nhiều lĩnh vực khác nhau. Dưới đây là một số ứng dụng nổi bật:

• Y học: Chất phóng xạ được sử dụng trong y học để điều trị và chẩn đoán bệnh. Ví dụ, đồng vị phóng xạ như I-131 được dùng để điều trị bệnh cường giáp hoặc ung thư tuyến giáp. Sự suy giảm độ phóng xạ theo thời gian giúp kiểm soát liều lượng an toàn cho bệnh nhân.
• Công nghiệp: Các đồng vị phóng xạ như Cobalt-60 được sử dụng trong việc kiểm tra không phá hủy các vật liệu, đặc biệt là trong ngành công nghiệp xây dựng và sản xuất. Nhờ vào kiến thức về độ phóng xạ, người ta có thể đánh giá mức độ suy giảm phóng xạ theo thời gian để đảm bảo an toàn và hiệu quả.
• Nông nghiệp: Phóng xạ cũng được sử dụng trong nông nghiệp để cải thiện năng suất và kiểm soát sâu bệnh. Ví dụ, các hạt phóng xạ được sử dụng để tiêu diệt côn trùng mà không cần sử dụng thuốc trừ sâu, nhờ vào khả năng tính toán chu kỳ bán rã để đảm bảo không còn phóng xạ nguy hiểm sau một thời gian nhất định.
• Nghiên cứu khoa học: Trong nghiên cứu, các nhà khoa học sử dụng đồng vị phóng xạ để theo dõi và nghiên cứu các phản ứng hóa học và sinh học. Sự hiểu biết về chu kỳ bán rã giúp họ dự đoán chính xác thời gian mà các đồng vị này sẽ mất đi hoạt tính phóng xạ, từ đó tối ưu hóa quy trình nghiên cứu.
• Quản lý chất thải phóng xạ: Hiểu biết về chu kỳ bán rã giúp định hướng quy trình lưu trữ và xử lý chất thải phóng xạ. Với mỗi loại chất thải, việc biết được thời gian mà độ phóng xạ giảm xuống mức an toàn là rất quan trọng để bảo vệ môi trường và con người.

Như vậy, kiến thức về độ phóng xạ không chỉ dừng lại ở lý thuyết mà có ảnh hưởng trực tiếp đến nhiều lĩnh vực trong cuộc sống. Việc áp dụng những nguyên lý này giúp cải thiện sức khỏe con người, tăng cường an toàn công nghiệp, và bảo vệ môi trường.

Để hiểu rõ hơn về các kiến thức liên quan đến độ phóng xạ và chu kỳ bán rã, bạn có thể tham khảo một số tài liệu và nguồn học tập sau đây:

• Các Trang Web Giáo Dục:
  1. : Đây là một trang web cung cấp các bài giảng chi tiết và lời giải cho các bài tập liên quan đến độ phóng xạ và chu kỳ bán rã. Trang web này đặc biệt hữu ích cho học sinh phổ thông với nhiều dạng bài tập và câu hỏi trắc nghiệm.
  2. : Một trang web học tập trực tuyến cung cấp các khóa học và tài liệu học tập từ lớp 6 đến lớp 12, với hơn 50,000 câu hỏi trắc nghiệm. Bạn có thể tìm thấy nhiều bài giải chi tiết về các vấn đề liên quan đến phóng xạ tại đây.
• Sách Và Bài Giảng Về Vật Lý Hạt Nhân:
  1. Physics for Scientists and Engineers của Raymond A. Serway và John W. Jewett: Cuốn sách này cung cấp kiến thức cơ bản và nâng cao về vật lý hạt nhân, bao gồm cả phần về phóng xạ và chu kỳ bán rã.
  2. Nuclear Physics: Principles and Applications của John Lilley: Đây là tài liệu tham khảo hữu ích cho những ai muốn nghiên cứu sâu hơn về vật lý hạt nhân và các ứng dụng của phóng xạ.

Ngoài ra, bạn có thể sử dụng các công cụ học trực tuyến như hoặc để tham gia các khóa học về vật lý và khoa học hạt nhân từ các trường đại học hàng đầu.

Hy vọng các tài liệu và nguồn học tập trên sẽ giúp bạn củng cố kiến thức và đạt được kết quả tốt trong quá trình học tập!