Phương Trình Chuyển Động và Phương Trình Quỹ Đạo: Khám Phá Toàn Diện và Ứng Dụng Thực Tiễn

Phương trình chuyển động và phương trình quỹ đạo là những khái niệm cơ bản trong vật lý học và toán học. Chúng mô tả sự thay đổi của vị trí và đường đi của các đối tượng trong không gian.

Phương Trình Chuyển Động

Phương trình chuyển động mô tả mối quan hệ giữa vị trí, tốc độ và gia tốc của một đối tượng theo thời gian. Có nhiều loại phương trình chuyển động khác nhau tùy thuộc vào loại chuyển động, bao gồm:

• Chuyển động thẳng đều: Vị trí của đối tượng được mô tả bằng phương trình: \( s = vt + s_0 \), trong đó \( s \) là vị trí, \( v \) là tốc độ, \( t \) là thời gian và \( s_0 \) là vị trí ban đầu.
• Chuyển động thẳng biến đổi đều: Vị trí của đối tượng được mô tả bằng phương trình: \( s = \frac{1}{2}at^2 + vt + s_0 \), trong đó \( a \) là gia tốc.

Phương Trình Quỹ Đạo

Phương trình quỹ đạo mô tả đường đi của đối tượng trong không gian. Đây là sự kết hợp của các phương trình chuyển động theo nhiều hướng khác nhau. Các phương trình quỹ đạo thường gặp bao gồm:

• Quỹ đạo hình parabol: Được mô tả bằng phương trình: \( y = ax^2 + bx + c \).
• Quỹ đạo hình elip: Được mô tả bằng phương trình: \( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \).

Ứng Dụng

Các phương trình chuyển động và quỹ đạo có ứng dụng rộng rãi trong nhiều lĩnh vực, từ kỹ thuật cơ khí, hàng không vũ trụ, đến các nghiên cứu khoa học cơ bản. Chúng giúp chúng ta hiểu rõ hơn về sự vận động của các đối tượng và dự đoán các hiện tượng tự nhiên.

Phương trình chuyển động là công cụ cơ bản trong cơ học, mô tả sự thay đổi vị trí của vật thể theo thời gian. Dưới đây là tổng quan về các loại phương trình chuyển động phổ biến:

Khái Niệm Cơ Bản

Phương trình chuyển động cung cấp thông tin về sự di chuyển của một vật thể dựa trên các yếu tố như vận tốc, gia tốc và thời gian. Nó có thể được chia thành hai loại chính: phương trình chuyển động thẳng đều và phương trình chuyển động thẳng biến đổi đều.

Phương Trình Chuyển Động Thẳng Đều

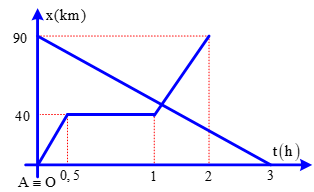
Phương trình chuyển động thẳng đều mô tả một vật thể di chuyển với vận tốc không thay đổi. Công thức cơ bản là:

  x(t) = x0 + v0 t

Trong đó, x(t) là vị trí tại thời điểm t, x₀ là vị trí ban đầu, v₀ là vận tốc không đổi, và t là thời gian.

Phương Trình Chuyển Động Thẳng Biến Đổi Đều

Phương trình chuyển động thẳng biến đổi đều mô tả sự di chuyển của vật thể với gia tốc không đổi. Công thức cơ bản là:

  x(t) = x0 + v0 t + \frac{1}{2} a t2

Trong đó, a là gia tốc, và các ký hiệu khác tương tự như trên.

Ứng Dụng trong Kỹ Thuật và Khoa Học

Phương trình chuyển động rất quan trọng trong các ứng dụng kỹ thuật và khoa học, chẳng hạn như trong thiết kế các hệ thống cơ học, phân tích chuyển động của các hành tinh, và dự đoán chuyển động của các vật thể trong không gian.

Phương trình quỹ đạo mô tả đường đi của một vật thể trong không gian khi nó bị tác động bởi các lực. Đây là một phần quan trọng trong động lực học, giúp hiểu rõ hơn về các chuyển động phức tạp của vật thể. Dưới đây là tổng quan về các loại phương trình quỹ đạo phổ biến:

Khái Niệm Cơ Bản

Quỹ đạo của một vật thể là đường đi mà vật thể đó theo đuổi trong không gian. Phương trình quỹ đạo có thể được phân loại dựa trên hình dạng của đường đi, bao gồm hình parabol, hình elip và hình hyperbol.

Phương Trình Quỹ Đạo Hình Parabol

Phương trình quỹ đạo hình parabol thường xuất hiện trong các tình huống như chuyển động của một vật thể bị ném lên hoặc rơi tự do dưới tác động của trọng lực. Công thức cơ bản là:

  y = x2 / (2a)

Trong đó, y là chiều cao của vật thể, x là khoảng cách ngang và a là độ dốc của quỹ đạo.

Phương Trình Quỹ Đạo Hình Elip

Quỹ đạo hình elip thường được áp dụng trong các chuyển động của các hành tinh quanh Mặt Trời. Công thức của quỹ đạo hình elip là:

  \frac{x2}{a2} + \frac{y2}{b2} = 1

Trong đó, a và b lần lượt là bán trục lớn và bán trục nhỏ của elip.

Ứng Dụng trong Vật Lý và Thiết Kế Kỹ Thuật

Phương trình quỹ đạo được ứng dụng rộng rãi trong vật lý để phân tích các hiện tượng như chuyển động của các hành tinh, đường đi của các vệ tinh, và thiết kế các hệ thống chuyển động trong kỹ thuật. Hiểu biết về các phương trình này giúp tối ưu hóa thiết kế và dự đoán chính xác các chuyển động.

Phương trình chuyển động và phương trình quỹ đạo đều là công cụ quan trọng trong cơ học và động lực học. Mặc dù chúng đều liên quan đến chuyển động của vật thể, chúng có sự khác biệt rõ ràng về cách mô tả và ứng dụng. Dưới đây là so sánh và phân tích giữa chúng:

Phương Trình Chuyển Động So Với Phương Trình Quỹ Đạo

• Phương Trình Chuyển Động: Mô tả sự thay đổi vị trí của một vật thể theo thời gian. Có thể là chuyển động thẳng đều hoặc thẳng biến đổi đều. Công thức cơ bản bao gồm:
  • Chuyển động thẳng đều: \( x(t) = x_0 + v_0 t \)
  • Chuyển động thẳng biến đổi đều: \( x(t) = x_0 + v_0 t + \frac{1}{2} a t^2 \)
• Phương Trình Quỹ Đạo: Mô tả hình dạng đường đi của một vật thể trong không gian dưới tác động của các lực. Có thể là hình parabol, elip, hoặc hyperbol. Công thức cơ bản bao gồm:
  • Hình parabol: \( y = \frac{x^2}{2a} \)
  • Hình elip: \( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \)

Ứng Dụng Thực Tiễn và Tầm Quan Trọng

• Phương Trình Chuyển Động: Được sử dụng để phân tích và dự đoán chuyển động của vật thể trong các tình huống như chuyển động của xe cộ, quỹ đạo của vệ tinh, và các bài toán cơ học cơ bản.
• Phương Trình Quỹ Đạo: Cần thiết cho việc thiết kế và phân tích các chuyển động phức tạp hơn như quỹ đạo của các hành tinh, đường đi của vật thể trong không gian, và các ứng dụng trong kỹ thuật hàng không và vũ trụ.

Khó Khăn và Giải Quyết Vấn Đề

• Phương Trình Chuyển Động: Có thể đơn giản và dễ áp dụng cho các tình huống cơ bản, nhưng có thể gặp khó khăn khi các điều kiện không ổn định hoặc có sự thay đổi nhanh chóng.
• Phương Trình Quỹ Đạo: Thường phức tạp hơn và yêu cầu kiến thức về hình học và lực học để giải quyết các vấn đề về quỹ đạo trong không gian, đặc biệt là khi có sự tương tác của nhiều lực.

Để nghiên cứu và hiểu rõ hơn về phương trình chuyển động và phương trình quỹ đạo, bạn có thể tham khảo các tài liệu sau đây:

Sách và Tài Liệu Giáo Khoa

• Đại Cương Về Cơ Học: Cung cấp kiến thức nền tảng về các loại chuyển động và quỹ đạo.
• Giải Tích Cơ Bản: Hướng dẫn chi tiết về các phương trình toán học liên quan đến chuyển động và quỹ đạo.
• Vật Lý Đại Cương: Giải thích các khái niệm cơ bản về lực và chuyển động, bao gồm cả phương trình quỹ đạo.

Các Tài Nguyên Trực Tuyến

• Khan Academy: Các bài giảng video và bài tập về cơ học và động lực học.
• MIT OpenCourseWare: Các khóa học miễn phí về vật lý và toán học liên quan đến chuyển động và quỹ đạo.
• Coursera: Các khóa học trực tuyến về cơ học và động lực học từ các trường đại học hàng đầu.

Video và Khóa Học

• Youtube - Khan Academy: Các video giảng dạy về phương trình chuyển động và quỹ đạo.
• edX: Các khóa học về vật lý và kỹ thuật, bao gồm cả phương trình quỹ đạo và ứng dụng của chúng.
• Udemy: Các khóa học trực tuyến về toán học và vật lý ứng dụng trong phân tích chuyển động.