Phát Biểu Định Luật Bảo Toàn Năng Lượng: Nguyên Lý Cơ Bản Của Vật Lý Học

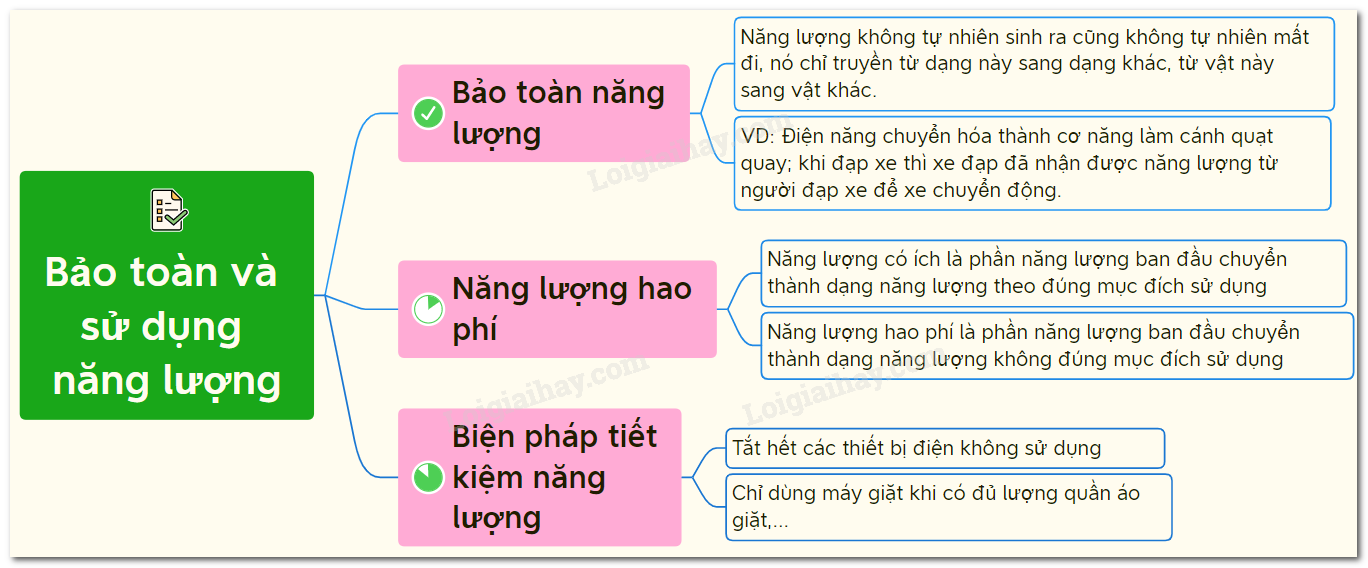
Định luật bảo toàn năng lượng là một trong những nguyên lý cơ bản của vật lý học, phát biểu rằng năng lượng không thể tự sinh ra hoặc mất đi mà chỉ có thể chuyển từ dạng này sang dạng khác hoặc được truyền từ hệ thống này sang hệ thống khác.

Chuyển Hóa Năng Lượng

Năng lượng có thể chuyển từ dạng này sang dạng khác, nhưng tổng năng lượng trong một hệ thống cô lập luôn không đổi. Ví dụ, năng lượng hóa học trong thức ăn được chuyển hóa thành năng lượng cơ học khi chúng ta di chuyển.

Hệ Thống Đóng và Hệ Thống Mở

Trong một hệ thống đóng, năng lượng không thể trao đổi với môi trường xung quanh, do đó tổng năng lượng của hệ thống luôn không đổi. Trong hệ thống mở, năng lượng có thể được trao đổi với môi trường, nhưng tổng năng lượng của hệ thống và môi trường vẫn không thay đổi.

Các Công Thức Liên Quan

• Động năng: \( E_k = \frac{1}{2}mv^2 \)
• Thế năng: \( E_p = mgh \)
• Nhiệt năng: \( Q = mc\Delta T \)
• Năng lượng điện từ: \( E = hf \)

Nguyên Lý Nhiệt Động Học

Định luật bảo toàn năng lượng cũng là cơ sở của nguyên lý nhiệt động học, đặc biệt là nguyên lý thứ nhất. Nguyên lý này phát biểu rằng sự thay đổi nội năng của một hệ thống bằng tổng nhiệt lượng truyền vào hệ thống và công hệ thống thực hiện.

Ứng Dụng Thực Tiễn

Định luật bảo toàn năng lượng có ứng dụng rộng rãi trong các lĩnh vực như kỹ thuật, cơ khí, điện lực, và nhiều ngành khoa học khác. Nhờ nguyên lý này, các công nghệ tiên tiến đã được phát triển để tối ưu hóa sử dụng năng lượng.

Bài Tập Vận Dụng

1. Một vật có khối lượng 10 gam, rơi tự do từ độ cao 5m. Tính cơ năng biết vận tốc rơi là 13 km/h và gia tốc trọng trường là 9,8 m/s².
2. Tính nhiệt lượng cần thiết để nâng nhiệt độ của 2 kg nước từ 20°C lên 100°C, biết nhiệt dung riêng của nước là 4.186 J/g°C.

Kết Luận

Định luật bảo toàn năng lượng không chỉ là một nguyên lý cơ bản giúp chúng ta hiểu rõ hơn về các hiện tượng tự nhiên, mà còn là nền tảng cho nhiều công nghệ và ứng dụng trong đời sống hàng ngày.

Định luật bảo toàn năng lượng là một nguyên lý cơ bản trong vật lý học, khẳng định rằng năng lượng trong một hệ kín không thể tự sinh ra hay tự mất đi, mà chỉ có thể chuyển hóa từ dạng này sang dạng khác. Nguyên lý này đóng vai trò quan trọng trong việc giải thích các hiện tượng tự nhiên và là nền tảng cho nhiều công trình nghiên cứu khoa học hiện đại.

Định luật được phát biểu như sau: "Tổng năng lượng trong một hệ cô lập luôn không đổi, dù cho các quá trình bên trong hệ có diễn ra như thế nào". Điều này có nghĩa là, trong mọi quá trình, tổng năng lượng đầu vào và đầu ra luôn bằng nhau, không có năng lượng nào bị thất thoát hay tự sinh ra.

Với tầm quan trọng của nó, định luật bảo toàn năng lượng không chỉ được áp dụng rộng rãi trong các lĩnh vực khoa học như vật lý, hóa học mà còn trong kỹ thuật, công nghệ và đời sống hàng ngày. Hiểu biết về nguyên lý này giúp chúng ta nắm bắt được cách thức mà năng lượng vận hành trong vũ trụ, từ đó có thể ứng dụng hiệu quả vào cuộc sống và sản xuất.

Định luật bảo toàn năng lượng là một trong những nguyên lý cơ bản nhất trong vật lý học, khẳng định rằng năng lượng không thể tự sinh ra hoặc mất đi mà chỉ có thể chuyển từ dạng này sang dạng khác. Nguyên lý này giải thích sự chuyển hóa năng lượng trong các hệ vật lý và được áp dụng rộng rãi trong nhiều lĩnh vực khoa học và kỹ thuật.

Về mặt toán học, định luật này có thể được diễn đạt qua biểu thức:

\[
E_{\text{tổng}} = E_{\text{đầu vào}} - E_{\text{đầu ra}}
\]

Trong đó:

• \( E_{\text{tổng}} \) là tổng năng lượng của hệ.
• \( E_{\text{đầu vào}} \) là năng lượng ban đầu.
• \( E_{\text{đầu ra}} \) là năng lượng cuối cùng sau quá trình chuyển hóa.

Nguyên lý bảo toàn năng lượng có thể thấy rõ trong các hiện tượng tự nhiên như chuyển động, sự phát nhiệt, và bức xạ. Ví dụ, trong quá trình rơi tự do của một vật, thế năng dần chuyển hóa thành động năng, nhưng tổng năng lượng của hệ vẫn không đổi.

Hiểu rõ nguyên lý này giúp chúng ta giải thích và dự đoán được các hiện tượng trong tự nhiên cũng như ứng dụng hiệu quả trong các lĩnh vực như sản xuất năng lượng, cơ khí, và công nghệ.

Định luật bảo toàn năng lượng áp dụng cho nhiều hiện tượng vật lý khác nhau và có thể được biểu diễn qua nhiều công thức liên quan. Dưới đây là một số công thức tiêu biểu:

• Công thức cơ bản: Tổng năng lượng trong một hệ cô lập là không đổi: \[ E_{\text{tổng}} = E_{\text{k} } + E_{\text{t} } = \text{hằng số} \] Trong đó:
  • \(E_{\text{k}}\): Động năng.
  • \(E_{\text{t}}\): Thế năng.
• Định luật bảo toàn cơ năng: Áp dụng cho chuyển động của các vật trong trường lực bảo toàn như trường trọng lực: \[ E_{\text{cơ}} = \frac{1}{2}mv^2 + mgh = \text{hằng số} \] Trong đó:
  • \(m\): Khối lượng của vật (kg).
  • \(v\): Vận tốc của vật (m/s).
  • \(h\): Độ cao của vật so với mốc thế năng (m).
  • \(g\): Gia tốc trọng trường (m/s²).
• Định luật bảo toàn năng lượng nhiệt: Trong quá trình truyền nhiệt giữa hai vật: \[ Q = mc\Delta T \] Trong đó:
  • \(Q\): Nhiệt lượng (J).
  • \(m\): Khối lượng của chất (kg).
  • \(c\): Nhiệt dung riêng của chất (J/kg.K).
  • \(\Delta T\): Độ biến thiên nhiệt độ (K).

Những công thức trên giúp chúng ta hiểu rõ hơn về cách năng lượng được bảo toàn và chuyển đổi trong các hệ thống vật lý khác nhau, từ đó áp dụng vào các bài toán và tình huống thực tế.

Định luật bảo toàn năng lượng là một nguyên lý cơ bản trong vật lý và có nhiều ứng dụng thực tiễn trong đời sống hàng ngày cũng như trong các ngành khoa học và kỹ thuật. Dưới đây là một số ứng dụng cụ thể của định luật này:

• Động cơ và máy móc: Định luật bảo toàn năng lượng là cơ sở cho việc thiết kế và vận hành các loại động cơ như động cơ nhiệt, động cơ đốt trong và động cơ điện. Năng lượng được chuyển hóa từ dạng này sang dạng khác để thực hiện công việc.
• Năng lượng tái tạo: Nguyên lý bảo toàn năng lượng được ứng dụng trong việc khai thác và sử dụng các nguồn năng lượng tái tạo như năng lượng mặt trời, gió và thủy điện. Ví dụ, trong các nhà máy thủy điện, năng lượng thế năng của nước được chuyển thành động năng và sau đó thành điện năng.
• Hệ thống điện lạnh: Trong các hệ thống điều hòa không khí và tủ lạnh, định luật bảo toàn năng lượng được áp dụng để tối ưu hóa quá trình làm lạnh. Nhiệt lượng được chuyển từ môi trường này sang môi trường khác, đảm bảo hiệu suất làm việc cao.
• Công nghiệp ô tô: Trong ngành công nghiệp ô tô, định luật bảo toàn năng lượng được sử dụng để tối ưu hóa hiệu suất nhiên liệu và giảm thiểu tiêu thụ năng lượng. Các hệ thống phanh tái tạo trên xe điện và xe hybrid là một ví dụ điển hình.
• Vũ trụ học và thiên văn học: Định luật này cũng được áp dụng trong nghiên cứu các hiện tượng vũ trụ như sự chuyển động của các hành tinh, ngôi sao và lỗ đen. Năng lượng được bảo toàn trong quá trình va chạm và tương tác giữa các thiên thể.

Nhờ vào định luật bảo toàn năng lượng, con người đã có thể phát triển nhiều công nghệ hiện đại, góp phần nâng cao chất lượng cuộc sống và khai thác hiệu quả các nguồn năng lượng trong tự nhiên.

Định luật bảo toàn năng lượng là một trong những nguyên lý cơ bản trong vật lý, có ứng dụng rộng rãi trong nhiều lĩnh vực. Dưới đây là một số dạng bài tập vận dụng định luật này, giúp học sinh nắm vững lý thuyết và thực hành tính toán hiệu quả.

5.1. Bài Tập Tính Toán Động Năng và Thế Năng

Động năng và thế năng là hai dạng năng lượng cơ bản liên quan đến định luật bảo toàn năng lượng. Các bài tập dưới đây giúp bạn áp dụng công thức tính toán động năng và thế năng trong các tình huống thực tế:

• Tính động năng \( W_d = \frac{1}{2} mv^2 \), trong đó:
  • \( m \): Khối lượng vật (kg).
  • \( v \): Vận tốc của vật (m/s).
• Tính thế năng trọng trường \( W_t = mgh \), trong đó:
  • \( m \): Khối lượng vật (kg).
  • \( g \): Gia tốc trọng trường (9.8 m/s²).
  • \( h \): Độ cao (m).

5.2. Bài Tập Ứng Dụng Trong Hệ Cơ Học

Các bài tập này yêu cầu sử dụng định luật bảo toàn cơ năng trong hệ cơ học. Ví dụ, tính toán sự chuyển hóa giữa động năng và thế năng trong các hệ kín như:

• Vật rơi tự do: Tính vận tốc của vật khi chạm đất dựa trên định luật bảo toàn cơ năng: \[ W_{\text{tổng}} = W_t + W_d = \text{const} \]
• Con lắc đơn: Tính vận tốc tại vị trí cân bằng và thế năng cực đại tại các vị trí biên.

5.3. Bài Tập Tính Toán Hiệu Suất

Hiệu suất là thước đo hiệu quả của một quá trình chuyển hóa năng lượng. Các bài tập tính toán hiệu suất thường yêu cầu công thức:
\[
\eta = \frac{P_{\text{có ích}}}{P_{\text{tổng}}} \times 100
\]
Trong đó, \( P_{\text{có ích}} \) là công suất có ích và \( P_{\text{tổng}} \) là công suất tiêu hao. Bạn có thể gặp bài tập như tính hiệu suất của một động cơ khi chuyển hóa nhiệt năng thành công cơ học.

5.4. Các Công Thức Tính Toán Năng Lượng Khác

Các công thức liên quan khác cần vận dụng trong các bài tập:

• Công suất: \( P = \frac{A}{t} \), trong đó:
  • \( A \): Công thực hiện (J).
  • \( t \): Thời gian (s).
• Công thức tính công: \( A = F \cdot s \cdot \cos{\alpha} \), trong đó:
  • \( F \): Lực tác dụng (N).
  • \( s \): Quãng đường dịch chuyển (m).
  • \( \alpha \): Góc giữa hướng lực và dịch chuyển.

Định luật bảo toàn năng lượng là một trong những nguyên lý quan trọng nhất của khoa học tự nhiên, được áp dụng rộng rãi trong nhiều lĩnh vực như vật lý, hóa học, và kỹ thuật. Nguyên lý này không chỉ giúp chúng ta hiểu rõ hơn về sự chuyển đổi năng lượng trong tự nhiên mà còn mở ra nhiều hướng nghiên cứu mới nhằm cải thiện chất lượng cuộc sống.

Qua quá trình phát triển, định luật này đã chứng minh được tính ổn định và vai trò không thể thiếu trong các hiện tượng vật lý. Năng lượng trong một hệ kín luôn được bảo toàn, dù nó có thể chuyển từ dạng này sang dạng khác, nhưng tổng năng lượng vẫn không đổi. Điều này tạo nền tảng cho sự phát triển các ngành công nghiệp và công nghệ hiện đại.

6.1. Vai Trò Của Định Luật Trong Vật Lý Học

Trong vật lý học, định luật bảo toàn năng lượng là cơ sở để giải thích các hiện tượng từ vi mô đến vĩ mô. Nó cho phép chúng ta tính toán và dự đoán kết quả của các hệ thống vật lý, từ chuyển động của vật thể đến sự tương tác giữa các hạt cơ bản. Định luật này cũng hỗ trợ trong việc xây dựng các mô hình khoa học chính xác hơn.

6.2. Ảnh Hưởng Đến Các Ngành Khoa Học Khác

Không chỉ dừng lại ở vật lý, định luật bảo toàn năng lượng còn có ảnh hưởng mạnh mẽ đến các ngành khoa học khác như hóa học, sinh học và cả môi trường. Trong hóa học, nó giúp giải thích các phản ứng và sự chuyển hóa năng lượng trong quá trình xảy ra phản ứng hóa học. Trong sinh học, định luật này giải thích cách năng lượng được truyền từ thực vật đến động vật trong các chuỗi thức ăn.

6.3. Tiềm Năng Nghiên Cứu và Phát Triển

Định luật bảo toàn năng lượng vẫn tiếp tục là nền tảng cho các nghiên cứu khoa học và phát triển công nghệ. Trong bối cảnh các nguồn năng lượng tái tạo ngày càng được ưu tiên, việc hiểu rõ và ứng dụng định luật này sẽ giúp chúng ta khai thác tối ưu các nguồn năng lượng sạch và bền vững.

Tóm lại, định luật bảo toàn năng lượng không chỉ là một nguyên lý lý thuyết mà còn là cơ sở cho nhiều ứng dụng thực tiễn. Việc nắm bắt và vận dụng đúng định luật này sẽ giúp chúng ta tiến xa hơn trong các nghiên cứu và cải tiến công nghệ, hướng đến một tương lai bền vững và hiệu quả hơn.