Lực đàn hồi lò xo: Định luật Húc và ứng dụng thực tiễn

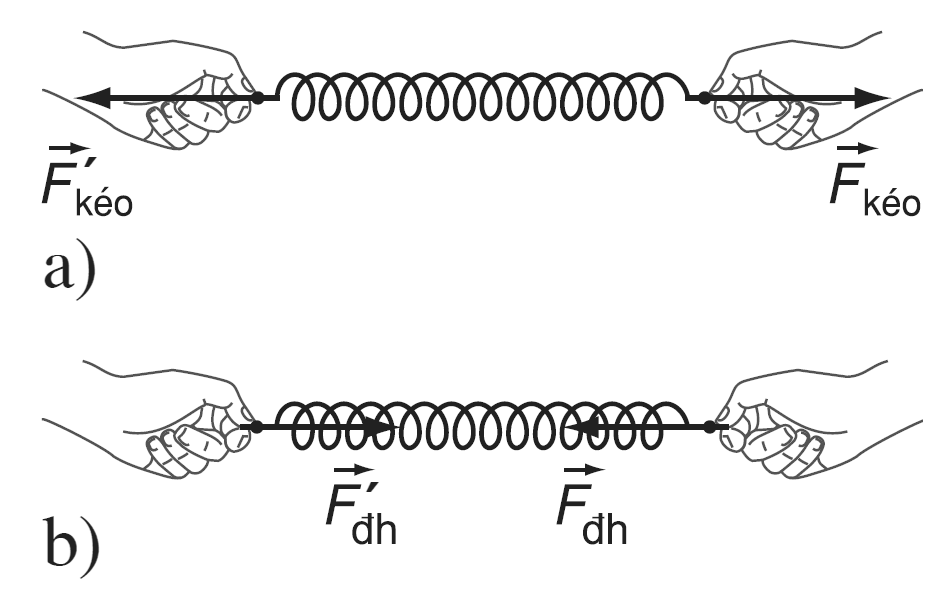
Lực đàn hồi của lò xo là một khái niệm quan trọng trong vật lý, đặc biệt là trong cơ học. Nó xuất hiện khi một lò xo bị biến dạng, có thể là dãn ra hoặc nén lại, do tác động của một lực ngoại lực. Lực đàn hồi của lò xo luôn có xu hướng đưa lò xo trở về trạng thái cân bằng ban đầu.

Định Luật Húc

Định luật Húc phát biểu rằng trong giới hạn đàn hồi, độ lớn của lực đàn hồi của lò xo tỉ lệ thuận với độ biến dạng của lò xo. Công thức của định luật Húc được biểu diễn như sau:

\( F_{dh} = k \cdot \Delta l \)

• \( F_{dh} \) là lực đàn hồi của lò xo (N)
• \( k \) là độ cứng (hay hệ số đàn hồi) của lò xo (N/m)
• \( \Delta l \) là độ biến dạng của lò xo (m)

Trong đó, độ cứng \( k \) là một hằng số đặc trưng cho mỗi lò xo, quyết định khả năng chống lại sự biến dạng của lò xo khi chịu lực tác dụng.

Các Dạng Bài Tập Liên Quan

Dạng 1: Tính lực đàn hồi khi treo vật

Khi treo một vật có khối lượng \( m \) vào lò xo, lực đàn hồi xuất hiện và cân bằng với trọng lực của vật:

\( F_{dh} = P = m \cdot g \)

Trong đó:

• \( P \) là trọng lực tác dụng lên vật (N)
• \( m \) là khối lượng của vật (kg)
• \( g \) là gia tốc trọng trường (m/s²)

Dạng 2: Cắt và ghép lò xo

Khi lò xo được cắt thành nhiều đoạn, độ cứng của các đoạn lò xo thay đổi theo chiều dài của mỗi đoạn. Nếu hai đoạn lò xo được ghép song song, độ cứng tổng cộng là tổng của độ cứng các đoạn:

\( k = k_1 + k_2 + \dots + k_n \)

Ngược lại, khi ghép nối tiếp, độ cứng tổng cộng giảm và được tính bằng công thức:

\( \frac{1}{k} = \frac{1}{k_1} + \frac{1}{k_2} + \dots + \frac{1}{k_n} \)

Ứng Dụng Thực Tế

Lực đàn hồi của lò xo có nhiều ứng dụng trong đời sống, từ các thiết bị giảm xóc trên xe máy, xe hơi, đến các loại cân lò xo hay đồng hồ cơ học. Lực đàn hồi giúp các thiết bị này hoạt động hiệu quả, đảm bảo độ bền và tính ổn định trong quá trình sử dụng.

Chú Ý

Đối với các vật liệu khác như dây cao su hay dây thép, lực đàn hồi cũng xuất hiện khi bị kéo dãn hoặc nén lại, tuy nhiên, đặc tính của lực đàn hồi trong các trường hợp này có thể khác biệt so với lò xo.

Lực đàn hồi của lò xo là một trong những khái niệm cơ bản trong vật lý, được ứng dụng rộng rãi trong nhiều lĩnh vực từ công nghiệp đến đời sống hàng ngày. Lực đàn hồi xuất hiện khi lò xo bị biến dạng do tác dụng của ngoại lực, và có xu hướng đưa lò xo trở về trạng thái ban đầu.

Lực đàn hồi của lò xo tuân theo định luật Húc, được biểu diễn qua công thức:

\[ F_{dh} = -k \cdot \Delta l \]

Trong đó:

• \( F_{dh} \): Lực đàn hồi (N)
• \( k \): Độ cứng của lò xo (N/m)
• \( \Delta l \): Độ biến dạng của lò xo (m)

Khi lò xo bị kéo dãn hoặc nén, lực đàn hồi sẽ tỉ lệ thuận với độ biến dạng của lò xo và có hướng ngược lại với hướng của ngoại lực tác dụng.

Ví dụ, khi một lò xo có độ cứng \( k = 100 \, \text{N/m} \) bị kéo dãn \( \Delta l = 0,05 \, \text{m} \), lực đàn hồi được tính như sau:

\[ F_{dh} = -100 \times 0,05 = -5 \, \text{N} \]

Như vậy, lực đàn hồi có giá trị 5 N và hướng về phía ngược lại với hướng kéo dãn.

Hiểu rõ lực đàn hồi lò xo giúp chúng ta ứng dụng nó hiệu quả trong các thiết bị cơ học, đồng hồ, và các hệ thống treo. Sự nghiên cứu về lực đàn hồi còn là nền tảng cho các thiết kế trong ngành công nghiệp sản xuất, xây dựng, và nhiều lĩnh vực khác.

Định luật Húc là một định luật cơ bản trong cơ học, phát biểu rằng lực đàn hồi của một lò xo tỉ lệ thuận với độ biến dạng của nó. Định luật này được phát hiện bởi nhà vật lý người Anh Robert Hooke vào năm 1676 và được biểu diễn bằng công thức:

$$ F = -k \cdot \Delta x $$

Trong đó:

• F là lực đàn hồi (đơn vị: Newton - N)
• k là hằng số đàn hồi của lò xo (đơn vị: N/m)
• Δx là độ biến dạng của lò xo so với chiều dài tự nhiên của nó (đơn vị: mét - m)

2.1. Phát biểu định luật Húc

Định luật Húc phát biểu rằng: "Lực đàn hồi sinh ra trong lò xo tỉ lệ thuận với độ biến dạng của nó và có chiều ngược với chiều của biến dạng." Điều này có nghĩa là nếu kéo dãn hoặc nén lò xo, lò xo sẽ sinh ra một lực ngược chiều để cố gắng trở về trạng thái cân bằng ban đầu.

2.2. Công thức tính lực đàn hồi

Công thức cơ bản của định luật Húc là:

$$ F = -k \cdot \Delta x $$

Ở đây:

• F là lực đàn hồi (N)
• k là hằng số đàn hồi của lò xo (N/m)
• Δx là độ biến dạng của lò xo so với chiều dài tự nhiên của nó (m)

Độ cứng của lò xo (hằng số k) phụ thuộc vào vật liệu và kết cấu của lò xo. Lò xo có giá trị k càng lớn thì càng cứng, lực đàn hồi sinh ra càng lớn khi bị biến dạng.

2.3. Các ví dụ và bài tập áp dụng định luật Húc

Để hiểu rõ hơn về định luật Húc, chúng ta có thể xem qua một số ví dụ và bài tập áp dụng:

1. Cho một lò xo có hằng số k = 200 N/m. Nếu lò xo bị kéo dãn ra 0,05 m, hãy tính lực đàn hồi của lò xo.
2. Một lò xo có hằng số k = 150 N/m bị nén lại 0,02 m. Hãy xác định lực đàn hồi mà lò xo này sinh ra.
3. Bài tập tổng hợp: Một lò xo có chiều dài tự nhiên là 0,3 m và hằng số đàn hồi là 250 N/m. Khi tác động một lực 50 N kéo dãn lò xo, hãy xác định chiều dài mới của lò xo.

Các bài tập này giúp bạn nắm vững cách áp dụng định luật Húc vào việc tính toán lực đàn hồi trong các tình huống thực tế.

3.1. Ứng dụng trong cơ học

Lực đàn hồi lò xo đóng vai trò quan trọng trong nhiều ứng dụng cơ học, từ các thiết bị đơn giản đến những hệ thống phức tạp. Các ứng dụng này dựa trên khả năng của lò xo biến đổi hình dạng khi chịu tác động của ngoại lực và trở lại hình dạng ban đầu khi lực tác động không còn.

• Hệ thống giảm xóc: Lò xo là thành phần quan trọng trong hệ thống giảm xóc của ô tô, xe máy. Chúng giúp hấp thụ lực va chạm, giảm rung lắc và mang lại sự êm ái khi di chuyển.
• Cân lò xo: Cân lò xo là một ứng dụng thực tiễn phổ biến, trong đó lực đàn hồi của lò xo được sử dụng để đo khối lượng của vật thông qua sự biến dạng của lò xo.
• Cơ cấu hồi chuyển: Trong các máy móc cơ khí, lò xo được sử dụng để hồi chuyển các cơ cấu về vị trí ban đầu sau khi đã thực hiện một hành động nào đó, chẳng hạn như trong các công tắc hoặc bàn đạp.

3.2. Ứng dụng trong đời sống hàng ngày

Lực đàn hồi lò xo không chỉ xuất hiện trong các thiết bị cơ học phức tạp mà còn hiện diện phổ biến trong nhiều vật dụng hàng ngày, mang lại sự tiện lợi và cải thiện chất lượng cuộc sống.

• Đệm lò xo: Lực đàn hồi của lò xo giúp đệm lò xo tạo ra cảm giác thoải mái khi nằm, phân tán áp lực cơ thể đều khắp mặt đệm, hỗ trợ giấc ngủ tốt hơn.
• Bút bi: Lò xo trong bút bi giúp cơ chế đẩy ngòi bút ra vào dễ dàng, tăng độ tiện lợi trong việc sử dụng hàng ngày.
• Ghế xoay: Trong các loại ghế xoay, lò xo hỗ trợ trong việc điều chỉnh độ cao và tạo sự linh hoạt khi sử dụng, giúp người ngồi cảm thấy thoải mái và giảm căng thẳng.
• Khóa cửa tự động: Lò xo trong khóa cửa giúp cơ chế khóa tự động hoạt động, đảm bảo an ninh mà không cần nhiều thao tác thủ công từ người dùng.

Trong phần này, chúng ta sẽ cùng thực hiện một số bài tập về lực đàn hồi của lò xo để củng cố kiến thức đã học. Các bài tập này bao gồm các dạng cơ bản như tính lực đàn hồi, xác định độ biến dạng của lò xo, và ứng dụng định luật Hooke vào các tình huống cụ thể.

1. Bài tập 1: Tính lực đàn hồi

   Một lò xo có độ cứng k = 200 N/m. Khi kéo dãn lò xo thêm 5 cm so với chiều dài ban đầu, hãy tính lực đàn hồi mà lò xo sinh ra.

   Giải:

   Sử dụng công thức định luật Hooke:

   \[
   F = k \times \Delta l
   \]

   Trong đó:

   • F: Lực đàn hồi (N)
   • k: Độ cứng của lò xo (N/m)
   • \(\Delta l\): Độ biến dạng của lò xo (m)

   Thay số vào công thức:

   \[
   F = 200 \times 0.05 = 10 \text{ N}
   \]

   Vậy lực đàn hồi của lò xo là 10 N.

2. Bài tập 2: Xác định độ biến dạng của lò xo

   Một lò xo có độ cứng k = 300 N/m. Khi tác dụng một lực 15 N lên lò xo, hãy xác định độ biến dạng của lò xo.

   Giải:

   Sử dụng công thức định luật Hooke:

   \[
   \Delta l = \frac{F}{k}
   \]

   Thay số vào công thức:

   \[
   \Delta l = \frac{15}{300} = 0.05 \text{ m} = 5 \text{ cm}
   \]

   Vậy độ biến dạng của lò xo là 5 cm.

3. Bài tập 3: Ứng dụng trong thực tế

   Một lò xo treo thẳng đứng có chiều dài tự nhiên là 20 cm. Khi treo một vật có khối lượng 1 kg vào lò xo, lò xo dãn thêm 4 cm. Tính độ cứng của lò xo.

   Giải:

   Lực tác dụng lên lò xo là trọng lực của vật:

   \[
   F = mg
   \]

   Trong đó:

   • m: Khối lượng của vật (kg)
   • g: Gia tốc trọng trường (≈ 9.8 m/s²)

   Thay số vào công thức:

   \[
   F = 1 \times 9.8 = 9.8 \text{ N}
   \]

   Sử dụng định luật Hooke để tính độ cứng của lò xo:

   \[
   k = \frac{F}{\Delta l} = \frac{9.8}{0.04} = 245 \text{ N/m}
   \]

   Vậy độ cứng của lò xo là 245 N/m.

Các bài tập trên giúp các em nắm vững cách tính lực đàn hồi và độ biến dạng của lò xo, từ đó có thể áp dụng vào các bài toán thực tế khác.

Việc học và áp dụng lực đàn hồi lò xo không chỉ giúp nắm vững lý thuyết mà còn cần chú ý đến các yếu tố thực tế để đảm bảo hiệu quả và an toàn. Dưới đây là một số lưu ý quan trọng:

• Nắm vững định luật Húc: Hiểu rõ định luật Húc, công thức tính lực đàn hồi $F\; =\; -k\backslash cdot\; \backslash Delta\; l$ trong đó k là độ cứng của lò xo và Δl là độ biến dạng của lò xo, sẽ giúp bạn áp dụng chính xác trong các bài toán.
• Giới hạn đàn hồi: Lò xo có một giới hạn đàn hồi nhất định. Nếu vượt quá giới hạn này, lò xo sẽ bị biến dạng vĩnh viễn và không trở về hình dạng ban đầu. Do đó, cần kiểm tra kỹ lò xo trước khi thực hiện các thí nghiệm.
• Tính toán độ cứng của lò xo: Khi làm các bài tập liên quan đến lực đàn hồi, cần phải xác định chính xác độ cứng k của lò xo. Độ cứng này có thể thay đổi tùy vào vật liệu và kích thước của lò xo, do đó cần đọc kỹ các thông số kỹ thuật hoặc kết quả thí nghiệm.
• Làm quen với các dạng bài tập: Hãy thực hành với các dạng bài tập khác nhau như tính lực đàn hồi, xác định độ biến dạng của lò xo dưới tác dụng của lực, và các bài toán kết hợp với các định luật khác.
• An toàn khi sử dụng lò xo: Khi tiến hành thí nghiệm, hãy luôn đảm bảo an toàn bằng cách kiểm tra chất lượng lò xo, tránh áp dụng lực quá lớn gây nguy hiểm, và đeo bảo hộ nếu cần thiết.
• Áp dụng vào thực tế: Lực đàn hồi của lò xo không chỉ giới hạn trong phòng thí nghiệm mà còn áp dụng rộng rãi trong các lĩnh vực như kỹ thuật, xây dựng và đời sống hàng ngày. Hãy tìm hiểu các ứng dụng thực tiễn để hiểu rõ hơn về vai trò của lực đàn hồi.

Những lưu ý trên sẽ giúp bạn học tập và áp dụng lực đàn hồi lò xo một cách hiệu quả và an toàn, đồng thời tạo nền tảng vững chắc cho các kiến thức vật lý nâng cao.

Qua quá trình học tập và nghiên cứu về lực đàn hồi của lò xo, chúng ta đã có được những hiểu biết sâu sắc về các khái niệm và định luật quan trọng trong vật lý. Lực đàn hồi là một trong những lực cơ bản, xuất hiện khi lò xo bị biến dạng dưới tác động của ngoại lực.

Trong suốt quá trình học, chúng ta đã khám phá:

• Khái niệm lực đàn hồi: Đây là lực xuất hiện khi lò xo bị kéo dãn hoặc nén lại, với độ lớn của lực tỉ lệ thuận với độ biến dạng của lò xo theo định luật Hooke. Lực đàn hồi có khả năng đưa lò xo trở về trạng thái cân bằng ban đầu.
• Định luật Hooke: Định luật này chỉ ra rằng lực đàn hồi F trong một lò xo tỉ lệ thuận với độ biến dạng Δl của nó, được biểu diễn bằng công thức:
  \[ F = -k \cdot \Delta l \] trong đó \( k \) là hệ số đàn hồi của lò xo.
• Ứng dụng thực tế: Lực đàn hồi được ứng dụng rộng rãi trong nhiều lĩnh vực của cuộc sống như trong các thiết bị cơ khí, xây dựng, và các hệ thống giảm chấn.

Việc nắm vững các kiến thức về lực đàn hồi không chỉ giúp chúng ta hiểu rõ hơn về các hiện tượng vật lý xung quanh, mà còn tạo nền tảng cho việc nghiên cứu các lĩnh vực khoa học và kỹ thuật liên quan. Hãy tiếp tục áp dụng và thực hành để làm chủ kiến thức này một cách hiệu quả.