Kính Hiển Vi 11: Tất Tần Tật Về Công Dụng, Cấu Tạo và Ứng Dụng

Kính hiển vi là một phần quan trọng trong chương trình Vật Lý lớp 11, được giảng dạy nhằm giúp học sinh hiểu về nguyên lý hoạt động và ứng dụng của kính hiển vi trong việc quan sát các vật thể nhỏ mà mắt thường không thể nhìn thấy được. Dưới đây là các nội dung chi tiết về chủ đề này.

1. Công dụng và cấu tạo của kính hiển vi

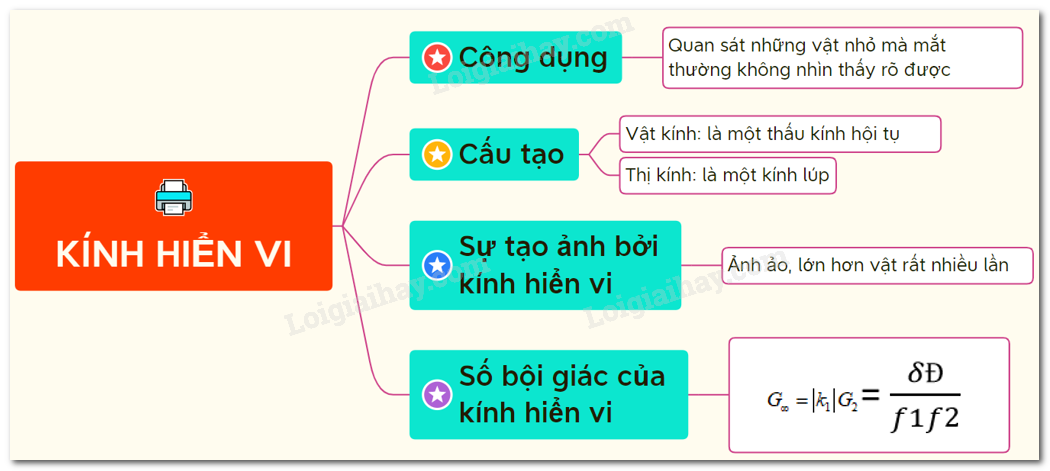
Kính hiển vi là dụng cụ quang học bổ trợ cho mắt để quan sát các vật rất nhỏ bằng cách tạo ra ảnh có góc trông lớn hơn. Cấu tạo cơ bản của kính hiển vi bao gồm:

• Vật kính: Là một thấu kính hội tụ có tiêu cự rất nhỏ (vài mm).
• Thị kính: Là thấu kính hội tụ có tiêu cự nhỏ hơn (vài cm) so với vật kính.
• Độ dài quang học: Ký hiệu là \( \delta \), là khoảng cách giữa ảnh và vật kính.
• Bộ phận tụ sáng: Thường là gương cầu lõm, giúp chiếu sáng vật cần quan sát.

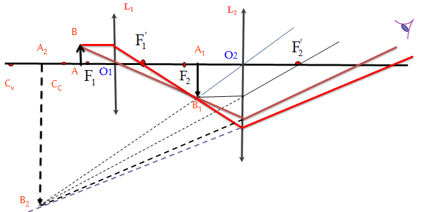
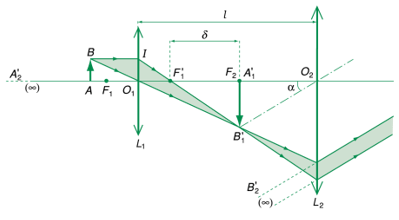
2. Sự tạo ảnh bởi kính hiển vi

Quá trình tạo ảnh bởi kính hiển vi diễn ra như sau:

• Vật kính tạo ra một ảnh thật \( A_{1}B_{1} \) lớn hơn so với vật gốc \( AB \).
• Thị kính tiếp tục phóng đại ảnh này, tạo ra một ảnh ảo \( A_{2}B_{2} \) mà mắt có thể quan sát.
• Điều chỉnh khoảng cách giữa vật và vật kính \( d_1 \) để ảnh cuối cùng xuất hiện trong giới hạn nhìn rõ của mắt.

Sơ đồ tạo ảnh:

\( \text{Vật } AB \rightarrow \text{Ảnh thật } A_{1}B_{1} \rightarrow \text{Ảnh ảo } A_{2}B_{2} \)

3. Số bội giác của kính hiển vi

Số bội giác \( G \) của kính hiển vi phụ thuộc vào khoảng cách ngắm chừng:

• Khi ngắm chừng ở cực cận, số bội giác được tính theo công thức:

\( G_C = \left| \frac{d_{1}^{'} d_{2}^{'}}{d_{1} d_{2}} \right| \)

• Khi ngắm chừng ở vô cực:

\( G_\infty = \left| k_{1} \right| G_{2} = \frac{\delta \cdot OCC}{f_{1} f_{2}} \)

4. Bài tập ứng dụng

Sau khi học xong lý thuyết về kính hiển vi, học sinh sẽ giải quyết các bài tập liên quan đến:

• Xác định ảnh tạo bởi thấu kính và hệ thấu kính.
• Tính toán độ bội giác của kính hiển vi trong các điều kiện khác nhau.

Các kiến thức này không chỉ giúp học sinh nắm vững lý thuyết mà còn ứng dụng thực tế trong các ngành khoa học nghiên cứu như sinh học, y học và công nghệ vật liệu.

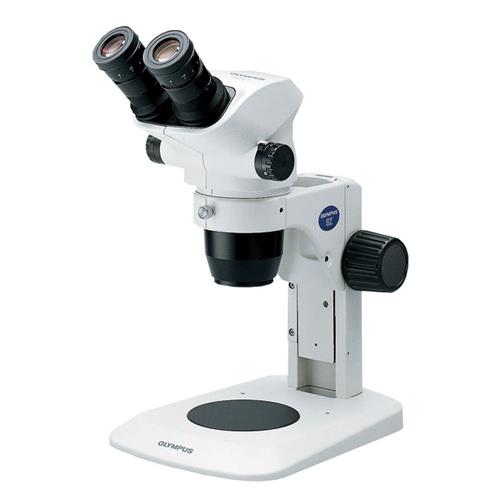
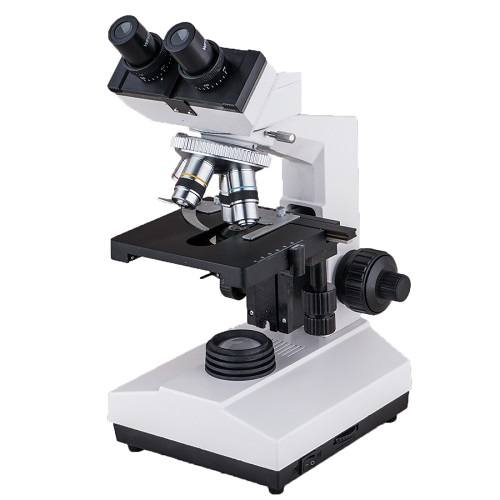
Kính hiển vi là một dụng cụ quang học quan trọng, có vai trò lớn trong việc quan sát các vật thể cực nhỏ mà mắt thường không thể nhìn thấy. Công dụng và cấu tạo của kính hiển vi được hiểu qua các thành phần và chức năng chính như sau:

• Công Dụng: Kính hiển vi giúp phóng đại hình ảnh của các đối tượng nhỏ, cho phép người sử dụng quan sát chi tiết mà không thể nhìn thấy bằng mắt thường. Điều này đặc biệt hữu ích trong các lĩnh vực như sinh học, y học và khoa học vật liệu.
• Cấu Tạo:
• Vật Kính: Là thấu kính hội tụ với tiêu cự rất nhỏ, thường chỉ vài mm. Vật kính là bộ phận quan trọng đầu tiên của kính hiển vi, có nhiệm vụ tạo ra một ảnh thật lớn hơn so với vật gốc.
• Thị Kính: Thị kính cũng là thấu kính hội tụ, nhưng có tiêu cự lớn hơn vật kính (vài cm). Thị kính phóng đại ảnh thật được tạo ra bởi vật kính để tạo thành ảnh ảo lớn hơn mà mắt có thể quan sát được.
• Bộ Phận Tụ Sáng: Gồm gương cầu lõm hoặc các bộ phận chiếu sáng khác, có nhiệm vụ tập trung ánh sáng lên vật cần quan sát, đảm bảo hình ảnh rõ nét.
• Độ Dài Quang Học: Ký hiệu là \( \delta \), là khoảng cách giữa ảnh và vật kính, đóng vai trò quyết định đến độ phóng đại và chất lượng của ảnh quan sát.
• Chân Đế và Thân Kính: Đây là các bộ phận cơ học, giúp cố định kính hiển vi và điều chỉnh khoảng cách giữa các thấu kính để có được ảnh tốt nhất.

Tổng kết lại, kính hiển vi là một thiết bị không thể thiếu trong nghiên cứu khoa học và giáo dục, giúp mở rộng tầm nhìn vào thế giới vi mô với những chi tiết cực kỳ nhỏ bé.

Kính hiển vi hoạt động dựa trên nguyên lý quang học, sử dụng hai thấu kính hội tụ để phóng đại hình ảnh của vật thể nhỏ, giúp quan sát rõ các chi tiết không thể nhìn thấy bằng mắt thường. Nguyên lý hoạt động của kính hiển vi được chia thành các bước sau:

• 1. Tạo ảnh bởi vật kính:

  Vật thể cần quan sát được đặt gần vật kính, một thấu kính hội tụ có tiêu cự nhỏ. Vật kính sẽ tạo ra một ảnh thật lớn hơn so với vật, ảnh này nằm ở phía đối diện của vật kính. Hình ảnh này được gọi là ảnh trung gian.

• 2. Phóng đại ảnh bởi thị kính:

  Ảnh trung gian từ vật kính sau đó được phóng đại thêm bởi thị kính, là một thấu kính hội tụ với tiêu cự lớn hơn vật kính. Thị kính tạo ra một ảnh ảo lớn hơn nhiều lần so với ảnh trung gian, giúp mắt người quan sát dễ dàng nhìn thấy chi tiết của vật thể.

• 3. Điều chỉnh khoảng cách và tiêu điểm:

  Người sử dụng có thể điều chỉnh khoảng cách giữa vật kính và vật thể, cũng như khoảng cách giữa vật kính và thị kính để đạt được độ phóng đại mong muốn và làm rõ hình ảnh. Khoảng cách này cũng ảnh hưởng đến vị trí và kích thước của ảnh cuối cùng.

• 4. Chiếu sáng vật thể:

  Hệ thống chiếu sáng, thường là gương cầu lõm hoặc nguồn sáng LED, tập trung ánh sáng vào vật thể, đảm bảo rằng ảnh quan sát được rõ ràng và sắc nét. Điều này rất quan trọng, đặc biệt khi quan sát các mẫu vật trong suốt hoặc rất nhỏ.

Qua các bước trên, kính hiển vi giúp biến những vật thể nhỏ bé trở nên rõ ràng hơn, cho phép chúng ta khám phá những chi tiết vi mô mà mắt thường không thể thấy được.

Số bội giác của kính hiển vi là chỉ số quan trọng đo lường khả năng phóng đại hình ảnh của vật thể nhỏ. Để tính số bội giác, chúng ta cần hiểu rõ về các yếu tố liên quan, bao gồm vật kính, thị kính, và khoảng cách quang học giữa chúng.

• Số bội giác tổng:

  Số bội giác tổng của kính hiển vi được xác định bởi công thức:

  \[ G = G_{1} \times G_{2} \]

  Trong đó:

  • \( G_{1} \) là số bội giác của vật kính, được tính bằng tỉ số giữa khoảng cách từ vật kính đến ảnh trung gian và tiêu cự của vật kính.
  • \( G_{2} \) là số bội giác của thị kính, được tính bằng tỉ số giữa khoảng cách nhìn rõ của mắt và tiêu cự của thị kính.
• Số bội giác khi ngắm chừng ở cực cận:

  Trong trường hợp ngắm chừng ở cực cận, số bội giác được tính bằng công thức:

  \[ G_C = \frac{\delta}{f_{1}} \times \frac{D}{f_{2}} \]

  Trong đó:

  • \( \delta \) là độ dài quang học của kính hiển vi.
  • \( f_{1} \) là tiêu cự của vật kính.
  • \( f_{2} \) là tiêu cự của thị kính.
  • \( D \) là khoảng cách nhìn rõ của mắt, thường là 25 cm.
• Số bội giác khi ngắm chừng ở vô cực:

  Khi ngắm chừng ở vô cực, mắt người quan sát được giảm thiểu sự điều tiết, và số bội giác được tính bằng công thức:

  \[ G_\infty = \frac{\delta \cdot D}{f_{1} \times f_{2}} \]

Số bội giác càng lớn, hình ảnh của vật thể được phóng đại càng rõ nét, giúp người sử dụng quan sát các chi tiết nhỏ một cách dễ dàng và chính xác hơn.

Dưới đây là một số bài tập liên quan đến kính hiển vi, giúp bạn củng cố kiến thức và áp dụng các nguyên lý quang học trong thực tế. Các bài tập được thiết kế từ cơ bản đến nâng cao, phù hợp với chương trình học lớp 11.

• Bài Tập 1: Tính số bội giác của kính hiển vi

  Cho biết tiêu cự của vật kính là \( f_{1} = 0,5 \, cm \) và tiêu cự của thị kính là \( f_{2} = 2 \, cm \). Độ dài quang học \( \delta \) của kính hiển vi là \( 16 \, cm \). Tính số bội giác khi ngắm chừng ở vô cực.

  Lời giải:

  \[ G_\infty = \frac{\delta \cdot D}{f_{1} \times f_{2}} = \frac{16 \cdot 25}{0,5 \times 2} = 400 \]

• Bài Tập 2: Xác định khoảng cách từ vật đến vật kính

  Một mẫu vật được đặt cách vật kính của kính hiển vi một khoảng \( l = 0,7 \, cm \). Vật kính có tiêu cự là \( f_{1} = 0,5 \, cm \). Tính khoảng cách từ vật kính đến ảnh thật của mẫu vật.

  Lời giải:

  Dùng công thức thấu kính:

  \[ \frac{1}{f_{1}} = \frac{1}{d} + \frac{1}{l} \]

  Thay số vào:

  \[ \frac{1}{0,5} = \frac{1}{d} + \frac{1}{0,7} \]

  Tìm được \( d = 1,4 \, cm \).

• Bài Tập 3: Tính khoảng cách từ thị kính đến mắt

  Với các thông số như bài tập 1, tính khoảng cách từ thị kính đến mắt để ảnh cuối cùng nằm tại vô cực khi người quan sát ngắm chừng ở cực cận.

  Lời giải:

  Khoảng cách từ thị kính đến mắt là khoảng cách nhìn rõ của mắt, \( D = 25 \, cm \).

Các bài tập trên giúp bạn hiểu rõ hơn về nguyên lý hoạt động và cách tính toán liên quan đến kính hiển vi, từ đó áp dụng vào các bài kiểm tra và thực tế.

Kính hiển vi là một công cụ quan trọng trong nhiều lĩnh vực khoa học và công nghiệp, giúp con người khám phá và hiểu rõ hơn về thế giới vi mô. Dưới đây là một số ứng dụng thực tế nổi bật của kính hiển vi:

• Sinh học và Y học:

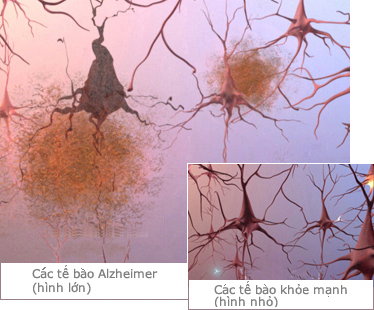
  Kính hiển vi được sử dụng để quan sát các tế bào, vi khuẩn, và virus, giúp các nhà khoa học và bác sĩ nghiên cứu cấu trúc tế bào, chẩn đoán bệnh lý, và phát triển các loại thuốc mới. Kính hiển vi điện tử còn giúp quan sát chi tiết ở cấp độ phân tử, mở ra những hiểu biết sâu sắc hơn về sự sống.

• Ngành công nghiệp vật liệu:

  Trong ngành công nghiệp vật liệu, kính hiển vi được sử dụng để kiểm tra và phân tích cấu trúc vi mô của kim loại, gốm sứ, và các hợp chất khác. Điều này giúp cải thiện chất lượng sản phẩm và phát triển các vật liệu mới với tính năng vượt trội.

• Nghiên cứu hóa học:

  Kính hiển vi hỗ trợ việc nghiên cứu cấu trúc hóa học của các chất, giúp hiểu rõ hơn về phản ứng hóa học và tạo ra các hợp chất mới. Kính hiển vi quang học và kính hiển vi điện tử đều có vai trò quan trọng trong việc phân tích cấu trúc tinh thể và các vật liệu nano.

• Giáo dục và đào tạo:

  Kính hiển vi là công cụ không thể thiếu trong giảng dạy và nghiên cứu tại các trường học và viện nghiên cứu. Nó giúp sinh viên và học sinh quan sát trực tiếp các hiện tượng sinh học và hóa học, từ đó hiểu rõ hơn về các khái niệm lý thuyết.

• Khoa học môi trường:

  Kính hiển vi cũng được sử dụng trong nghiên cứu môi trường để phân tích mẫu nước, đất, và không khí, xác định sự hiện diện của vi sinh vật và các chất ô nhiễm. Điều này giúp bảo vệ môi trường và sức khỏe cộng đồng.

Nhờ các ứng dụng thực tế đa dạng, kính hiển vi đã trở thành một công cụ không thể thiếu, góp phần quan trọng trong sự tiến bộ của khoa học và công nghệ.