Khi góc tới tăng hai lần thì góc khúc xạ thay đổi thế nào? Khám phá ngay!

Trong lĩnh vực quang học, khi ánh sáng truyền từ môi trường này sang môi trường khác, hiện tượng khúc xạ xảy ra. Hiện tượng này tuân theo định luật khúc xạ ánh sáng, còn được gọi là định luật Snell.

1. Định luật Snell

Định luật Snell mô tả mối quan hệ giữa góc tới (\(i\)) và góc khúc xạ (\(r\)) thông qua chỉ số chiết suất của hai môi trường. Công thức tổng quát của định luật Snell là:

\[
n_1 \sin{i} = n_2 \sin{r}
\]

Trong đó:

• \(n_1\): Chiết suất của môi trường ban đầu (môi trường mà ánh sáng đi vào).
• \(n_2\): Chiết suất của môi trường thứ hai (môi trường mà ánh sáng truyền qua).
• \(i\): Góc tới (góc tạo bởi tia tới và pháp tuyến tại điểm tới).
• \(r\): Góc khúc xạ (góc tạo bởi tia khúc xạ và pháp tuyến).

2. Ảnh hưởng của việc tăng góc tới lên hai lần đến góc khúc xạ

Khi góc tới (\(i\)) tăng gấp đôi, góc khúc xạ (\(r\)) không tăng gấp đôi theo. Thay vào đó, mối quan hệ giữa góc tới và góc khúc xạ được xác định bằng công thức của định luật Snell. Sự thay đổi của góc khúc xạ phụ thuộc vào giá trị của góc tới ban đầu và chỉ số chiết suất của các môi trường.

Giả sử ban đầu góc tới là \(i_1\) và sau khi tăng gấp đôi, góc tới trở thành \(i_2 = 2i_1\). Khi đó, tỉ lệ giữa góc khúc xạ mới và cũ có thể được mô tả bằng công thức:

\[
\frac{\sin{r_2}}{\sin{r_1}} = \frac{n_1 \sin{2i_1}}{n_1 \sin{i_1}} = \frac{2\sin{i_1}\cos{i_1}}{\sin{i_1}} = 2\cos{i_1}
\]

Điều này có nghĩa là tỉ lệ giữa sin của góc khúc xạ mới và cũ phụ thuộc vào cos của góc tới ban đầu. Do đó, góc khúc xạ mới có thể tăng, giảm hoặc giữ nguyên tùy thuộc vào giá trị của góc tới ban đầu.

3. Ví dụ minh họa

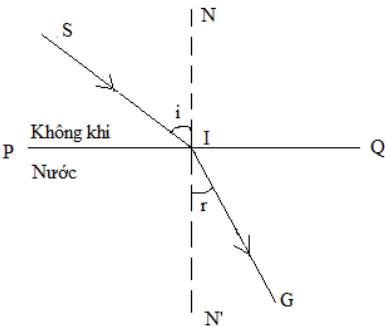
Giả sử ánh sáng đi từ không khí vào nước với chiết suất \(n_1 = 1\) (không khí) và \(n_2 = 1.33\) (nước). Nếu góc tới ban đầu là \(30^\circ\), ta có thể tính được góc khúc xạ ban đầu \(r_1\) bằng cách áp dụng định luật Snell:

\[
\sin{r_1} = \frac{n_1}{n_2} \sin{30^\circ} = \frac{1}{1.33} \times 0.5 \approx 0.376
\]

Từ đó, góc khúc xạ \(r_1 \approx 22^\circ\).

Nếu góc tới tăng lên \(60^\circ\), góc khúc xạ \(r_2\) sẽ được tính như sau:

\[
\sin{r_2} = \frac{1}{1.33} \sin{60^\circ} \approx 0.652
\]

Từ đó, góc khúc xạ \(r_2 \approx 40^\circ\).

4. Kết luận

Việc tăng gấp đôi góc tới không dẫn đến việc tăng gấp đôi góc khúc xạ. Mối quan hệ giữa góc tới và góc khúc xạ là phi tuyến tính và phụ thuộc vào chiết suất của các môi trường. Để tính chính xác góc khúc xạ, cần áp dụng đúng công thức của định luật Snell.

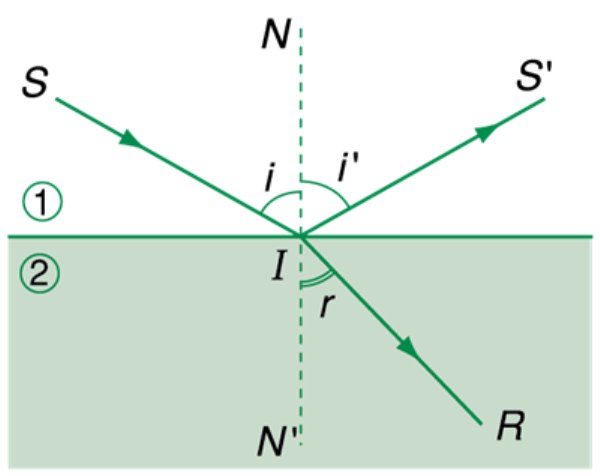
Định luật khúc xạ ánh sáng là một trong những nguyên lý cơ bản trong quang học, mô tả cách thức mà ánh sáng thay đổi hướng khi truyền qua các môi trường khác nhau. Định luật này được phát biểu như sau:

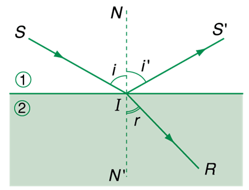
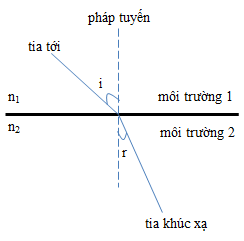
• Tia khúc xạ nằm trong mặt phẳng chứa tia tới và pháp tuyến tại điểm tới.
• Tỉ số giữa sin của góc tới và sin của góc khúc xạ là một hằng số, phụ thuộc vào chỉ số chiết suất của hai môi trường.

Công thức toán học của định luật khúc xạ, hay còn gọi là định luật Snell, được biểu diễn như sau:

\[
n_1 \sin{i} = n_2 \sin{r}
\]

Trong đó:

• \(n_1\) là chiết suất của môi trường mà tia sáng ban đầu truyền qua.
• \(n_2\) là chiết suất của môi trường mà tia sáng truyền vào.
• \(i\) là góc tới, được đo giữa tia tới và pháp tuyến tại điểm tới.
• \(r\) là góc khúc xạ, được đo giữa tia khúc xạ và pháp tuyến.

Điều này có nghĩa là, khi ánh sáng đi từ môi trường có chiết suất thấp sang môi trường có chiết suất cao, góc khúc xạ sẽ nhỏ hơn góc tới, và ngược lại. Định luật này là cơ sở cho nhiều ứng dụng quan trọng trong quang học, chẳng hạn như trong thiết kế thấu kính, kính mắt, và các thiết bị quang học khác.

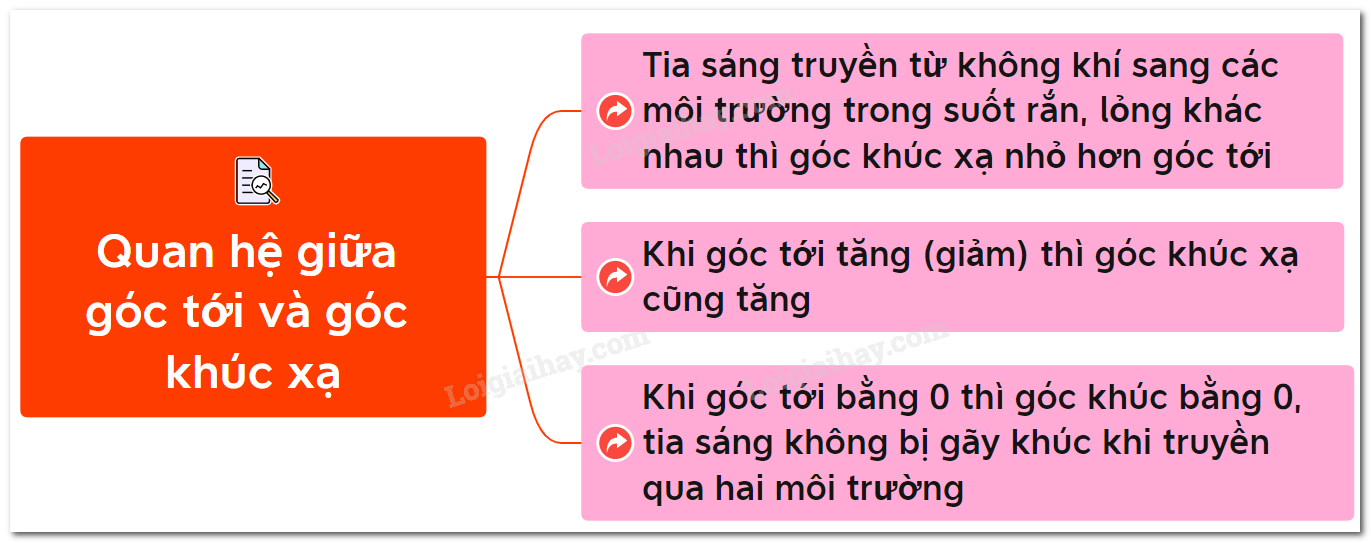
Khi góc tới (\(i\)) tăng lên, góc khúc xạ (\(r\)) sẽ thay đổi theo một quy luật nhất định dựa trên định luật khúc xạ ánh sáng (định luật Snell). Tuy nhiên, sự thay đổi này không hoàn toàn tỷ lệ thuận, mà còn phụ thuộc vào các yếu tố như chiết suất của các môi trường.

• Khi góc tới nhỏ: Góc khúc xạ sẽ lớn hơn góc tới. Nếu góc tới tăng, góc khúc xạ cũng tăng, nhưng tốc độ tăng của góc khúc xạ sẽ chậm hơn so với góc tới.
• Khi góc tới lớn: Khi góc tới tiếp cận gần \(90^\circ\), góc khúc xạ sẽ có xu hướng tiếp cận một giá trị cụ thể, và sự thay đổi góc khúc xạ trở nên rất nhỏ.

Để minh họa rõ hơn, ta xét một ví dụ cụ thể. Giả sử ánh sáng đi từ không khí (\(n_1 = 1\)) vào nước (\(n_2 = 1.33\)). Khi góc tới tăng từ \(30^\circ\) lên \(60^\circ\), góc khúc xạ sẽ thay đổi theo:

• Góc tới ban đầu \(i_1 = 30^\circ\), áp dụng định luật Snell:

\[ \sin{r_1} = \frac{n_1}{n_2} \sin{30^\circ} = \frac{1}{1.33} \times 0.5 \approx 0.376 \]

Góc khúc xạ \(r_1 \approx 22^\circ\).

• Khi góc tới tăng lên \(i_2 = 60^\circ\), góc khúc xạ \(r_2\) được tính như sau:

\[ \sin{r_2} = \frac{1}{1.33} \sin{60^\circ} \approx 0.652 \]

Góc khúc xạ \(r_2 \approx 40^\circ\).

Như vậy, khi góc tới tăng lên gấp đôi, góc khúc xạ tăng lên nhưng không gấp đôi. Điều này cho thấy mối quan hệ phi tuyến giữa góc tới và góc khúc xạ, thể hiện rõ ràng qua các ví dụ tính toán cụ thể.

Định luật khúc xạ ánh sáng không chỉ là một nguyên lý cơ bản trong vật lý học, mà còn có nhiều ứng dụng quan trọng trong đời sống và công nghệ. Dưới đây là một số ứng dụng điển hình:

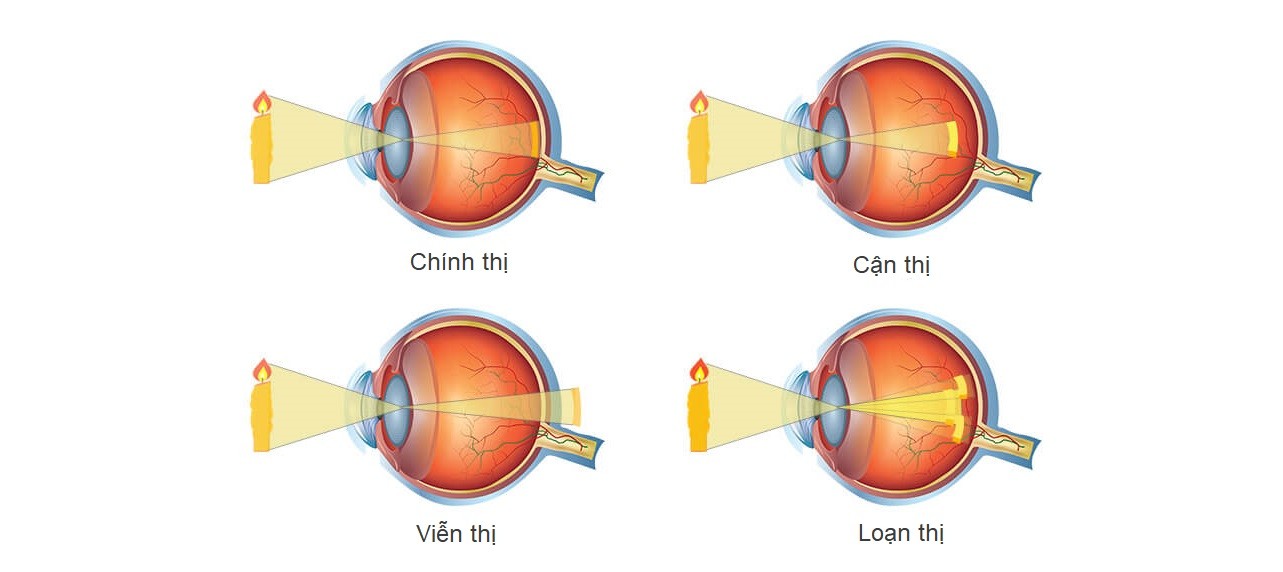
• Thiết kế thấu kính và kính mắt: Định luật khúc xạ được sử dụng để thiết kế các loại thấu kính hội tụ và phân kỳ, giúp điều chỉnh tầm nhìn của mắt người. Kính cận, kính viễn, và kính lão đều dựa trên nguyên lý này để điều chỉnh ánh sáng đi qua mắt, cải thiện thị lực.
• Thiết bị quang học: Các thiết bị quang học như kính hiển vi, kính viễn vọng, và máy ảnh đều tận dụng định luật khúc xạ để hội tụ hoặc phân tán ánh sáng, tạo ra hình ảnh rõ nét và chi tiết.
• Công nghệ sợi quang: Trong truyền thông hiện đại, sợi quang là một ứng dụng quan trọng của khúc xạ ánh sáng. Ánh sáng được dẫn truyền qua sợi quang nhờ hiện tượng phản xạ toàn phần, một hiện tượng liên quan chặt chẽ đến định luật khúc xạ.
• Thiết kế các thiết bị đo lường: Máy đo chiết suất (refractometer) sử dụng định luật khúc xạ để đo chỉ số chiết suất của các chất lỏng, hỗ trợ trong các ngành công nghiệp như thực phẩm, hóa học và y học.
• Hiện tượng cầu vồng: Cầu vồng là một hiện tượng tự nhiên, trong đó ánh sáng mặt trời bị khúc xạ và phản xạ trong các giọt nước mưa, tạo ra dải màu sắc rực rỡ trên bầu trời. Đây là minh chứng rõ ràng cho định luật khúc xạ trong tự nhiên.

Nhờ hiểu rõ và áp dụng định luật khúc xạ ánh sáng, con người đã phát triển nhiều công nghệ quan trọng, từ việc cải thiện chất lượng cuộc sống đến mở rộng khả năng khám phá thế giới xung quanh.

Để hiểu rõ hơn về định luật khúc xạ ánh sáng và ảnh hưởng của việc tăng góc tới lên góc khúc xạ, bạn có thể tham khảo một số câu hỏi và bài tập dưới đây. Những bài tập này sẽ giúp củng cố kiến thức và khả năng áp dụng lý thuyết vào thực tiễn.

Câu hỏi lý thuyết

• Trình bày định luật khúc xạ ánh sáng. Công thức của định luật này là gì?
• Giải thích tại sao khi góc tới tăng thì góc khúc xạ cũng tăng, nhưng không tỷ lệ thuận?
• Trong trường hợp nào góc khúc xạ bằng góc tới? Hãy mô tả các điều kiện cụ thể.

Bài tập tính toán

1. Ánh sáng truyền từ không khí vào nước với góc tới \(i = 45^\circ\). Hãy tính góc khúc xạ \(r\), biết chiết suất của không khí là \(n_1 = 1\) và của nước là \(n_2 = 1.33\).

   Hướng dẫn: Áp dụng định luật Snell \[n_1 \sin{i} = n_2 \sin{r}\] để tìm ra góc khúc xạ \(r\).

2. Một tia sáng đi từ thủy tinh có chiết suất \(n_1 = 1.5\) vào một môi trường không xác định với góc tới \(30^\circ\) và góc khúc xạ \(r = 22^\circ\). Hãy tính chiết suất của môi trường đó.

   Hướng dẫn: Sử dụng công thức \[n_2 = \frac{n_1 \sin{i}}{\sin{r}}\] để tính chiết suất của môi trường thứ hai.

3. Ánh sáng đi từ nước (\(n_1 = 1.33\)) vào thủy tinh (\(n_2 = 1.5\)) với góc tới ban đầu là \(25^\circ\). Nếu góc tới tăng lên \(50^\circ\), hãy tính góc khúc xạ tương ứng.

   Hướng dẫn: Tính góc khúc xạ cho từng góc tới và so sánh kết quả để thấy sự thay đổi.

Những câu hỏi và bài tập trên sẽ giúp bạn làm quen với cách áp dụng định luật khúc xạ ánh sáng vào các tình huống thực tế, đồng thời rèn luyện kỹ năng tính toán và tư duy logic.