Khi đặt một hiệu điện thế U vào hai đầu: Những khái niệm và ứng dụng quan trọng

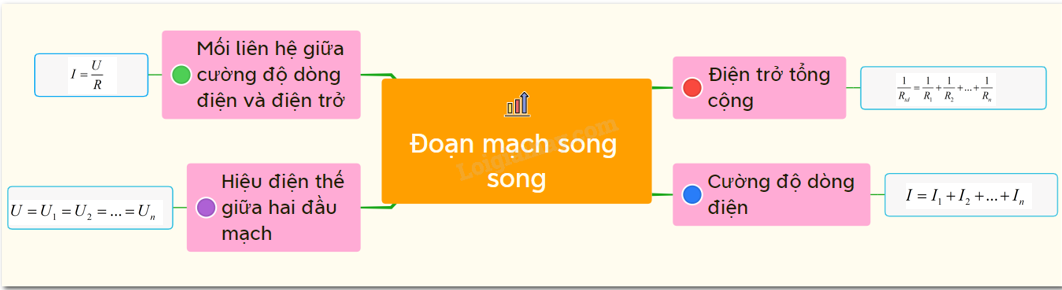
Khi đặt một hiệu điện thế \( U \) vào hai đầu một mạch điện, chúng ta có thể phân tích và tính toán các thông số khác nhau của mạch như dòng điện \( I \), công suất \( P \), và hiệu điện thế hiệu dụng \( U_\text{rms} \). Dưới đây là một số thông tin quan trọng về các loại mạch điện khác nhau và cách chúng hoạt động khi có hiệu điện thế đặt vào.

1. Mạch điện trở \( R \)

Khi đặt một hiệu điện thế \( U \) vào hai đầu một điện trở \( R \), dòng điện chạy qua điện trở có cường độ được tính theo định luật Ohm:

\[
I = \frac{U}{R}
\]

Công suất tiêu thụ trên điện trở được tính bằng công thức:

\[
P = U \cdot I = \frac{U^2}{R}
\]

2. Mạch RLC không phân nhánh

Trong một mạch RLC không phân nhánh, hiệu điện thế đặt vào mạch có dạng sóng hình sin \( U = U_0 \sin(\omega t) \). Tổng trở \( Z \) của mạch được tính bằng:

\[
Z = \sqrt{R^2 + (X_L - X_C)^2}
\]

trong đó \( X_L = \omega L \) là cảm kháng và \( X_C = \frac{1}{\omega C} \) là dung kháng. Dòng điện chạy qua mạch được tính bởi:

\[
I = \frac{U_0}{Z}
\]

Hiệu điện thế trên các phần tử R, L, C trong mạch là:

• Trên điện trở \( R \): \( U_R = I \cdot R \)
• Trên cuộn cảm \( L \): \( U_L = I \cdot X_L \)
• Trên tụ điện \( C \): \( U_C = I \cdot X_C \)

3. Các ứng dụng thực tiễn

Hiệu điện thế và dòng điện trong mạch điện có nhiều ứng dụng thực tiễn như:

1. Điều khiển các thiết bị điện gia dụng như đèn, quạt, máy tính.
2. Thiết kế và phân tích các mạch điện trong kỹ thuật điện tử.
3. Tính toán và kiểm soát công suất tiêu thụ trong hệ thống điện.

4. Ví dụ thực tế

Giả sử đặt một hiệu điện thế 6V vào hai đầu một điện trở 10Ω, cường độ dòng điện qua điện trở này sẽ là:

\[
I = \frac{6V}{10\Omega} = 0.6A
\]

Công suất tiêu thụ trên điện trở sẽ là:

\[
P = 6V \cdot 0.6A = 3.6W
\]

Những công thức và ví dụ trên giúp bạn hiểu rõ hơn về cách hoạt động của mạch điện khi đặt một hiệu điện thế \( U \) vào hai đầu. Hãy áp dụng những kiến thức này để phân tích và thiết kế mạch điện trong thực tế.

Định luật Ohm là một trong những định luật cơ bản trong lĩnh vực điện học, được phát biểu rằng dòng điện \( I \) chạy qua một điện trở \( R \) trong mạch tỉ lệ thuận với hiệu điện thế \( U \) đặt vào hai đầu của nó. Công thức của định luật Ohm được viết như sau:

\[
I = \frac{U}{R}
\]

Dưới đây là các bước cơ bản để áp dụng định luật Ohm trong mạch điện trở:

1. Xác định giá trị của điện trở \( R \) trong mạch. Điện trở có thể được cung cấp dưới dạng giá trị cố định hoặc có thể tính toán dựa trên các thông số của vật liệu và hình dạng.
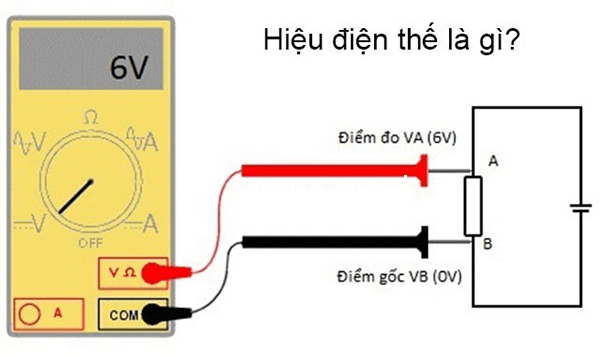
2. Đo hoặc xác định hiệu điện thế \( U \) đặt vào hai đầu của điện trở. Hiệu điện thế có thể được cung cấp từ một nguồn điện, như pin hoặc máy phát điện.
3. Sử dụng công thức \( I = \frac{U}{R} \) để tính toán dòng điện \( I \) chạy qua điện trở. Đây là dòng điện liên tục trong mạch điện một chiều (DC) và có thể thay đổi nếu mạch có các yếu tố khác như cuộn cảm hoặc tụ điện.
4. Kiểm tra công suất tiêu thụ trên điện trở bằng công thức:

\[
P = U \cdot I = \frac{U^2}{R}
\]

5. Đảm bảo rằng các giá trị dòng điện và công suất nằm trong giới hạn an toàn của các thành phần mạch để tránh hư hỏng.

Một số ví dụ điển hình của định luật Ohm bao gồm việc tính toán dòng điện qua một bóng đèn đơn giản trong mạch điện gia đình, hay xác định điện trở của một dây dẫn trong các ứng dụng công nghiệp.

Mạch RLC là một mạch điện bao gồm ba thành phần chính: điện trở \( R \), cuộn cảm \( L \), và tụ điện \( C \). Đây là một mạch cơ bản trong kỹ thuật điện tử, được sử dụng rộng rãi để phân tích các hệ thống có tính năng lọc, cộng hưởng và nhiều ứng dụng khác. Khi đặt một hiệu điện thế \( U \) vào mạch RLC, nhiều hiện tượng quan trọng xảy ra và chúng ta có thể tính toán được các thông số liên quan.

1. Tổng trở của mạch RLC

Tổng trở \( Z \) của mạch RLC là một đại lượng tổng hợp từ điện trở, cảm kháng và dung kháng. Nó được xác định bởi công thức:

\[
Z = \sqrt{R^2 + (X_L - X_C)^2}
\]

Trong đó:

• \( X_L = \omega L \) là cảm kháng, phụ thuộc vào tần số góc \( \omega \) và độ tự cảm \( L \).
• \( X_C = \frac{1}{\omega C} \) là dung kháng, phụ thuộc vào tần số góc \( \omega \) và điện dung \( C \).

2. Dòng điện trong mạch RLC

Khi đặt một hiệu điện thế \( U \) vào hai đầu mạch RLC, dòng điện \( I \) trong mạch có thể được tính bằng công thức:

\[
I = \frac{U}{Z}
\]

Do tổng trở \( Z \) phụ thuộc vào tần số, nên dòng điện trong mạch cũng sẽ thay đổi theo tần số của nguồn điện.

3. Hiệu điện thế trên các phần tử R, L, C

Hiệu điện thế trên từng phần tử trong mạch RLC có thể được tính như sau:

• Trên điện trở \( R \): \( U_R = I \cdot R \).
• Trên cuộn cảm \( L \): \( U_L = I \cdot X_L \).
• Trên tụ điện \( C \): \( U_C = I \cdot X_C \).

Trong trường hợp mạch RLC được sử dụng để lọc hoặc tạo cộng hưởng, giá trị tần số tại đó \( X_L \) và \( X_C \) bù trừ lẫn nhau là rất quan trọng. Ở tần số cộng hưởng, khi \( X_L = X_C \), tổng trở của mạch chỉ còn là \( R \), và dòng điện trong mạch đạt cực đại.

Mạch RLC có nhiều ứng dụng trong các hệ thống điện tử, từ lọc tín hiệu đến điều chỉnh tần số và giảm nhiễu trong các thiết bị điện tử hiện đại.

Hiệu điện thế \( U \) là một khái niệm cơ bản trong điện học, được ứng dụng rộng rãi trong nhiều lĩnh vực từ đời sống hàng ngày đến công nghiệp và nghiên cứu khoa học. Dưới đây là một số ứng dụng thực tiễn quan trọng của hiệu điện thế:

1. Điều khiển các thiết bị điện gia dụng

Hiệu điện thế là yếu tố quan trọng trong việc vận hành các thiết bị điện gia dụng như đèn, quạt, tủ lạnh, và máy giặt. Khi đặt một hiệu điện thế phù hợp vào hai đầu thiết bị, dòng điện sẽ chạy qua và thực hiện các chức năng của thiết bị đó. Việc lựa chọn hiệu điện thế đúng là cần thiết để đảm bảo thiết bị hoạt động hiệu quả và an toàn.

2. Thiết kế và phân tích mạch điện tử

Trong lĩnh vực điện tử, hiệu điện thế được sử dụng để phân tích và thiết kế các mạch điện tử. Hiệu điện thế được đặt vào các linh kiện như transistor, diode, và IC để điều khiển dòng điện và thực hiện các chức năng phức tạp trong các thiết bị điện tử hiện đại, từ điện thoại di động đến máy tính.

3. Kiểm soát và điều chỉnh công suất tiêu thụ

Trong hệ thống điện, hiệu điện thế được sử dụng để kiểm soát và điều chỉnh công suất tiêu thụ. Bằng cách điều chỉnh hiệu điện thế, các kỹ sư có thể thay đổi dòng điện và do đó điều chỉnh công suất của các thiết bị và hệ thống điện. Điều này rất quan trọng trong việc tối ưu hóa hiệu suất và giảm thiểu tổn thất năng lượng trong các hệ thống truyền tải và phân phối điện.

4. Ứng dụng trong công nghiệp và y tế

Trong công nghiệp, hiệu điện thế được sử dụng để điều khiển các máy móc và thiết bị tự động hóa. Trong y tế, các thiết bị chẩn đoán và điều trị như máy đo điện tâm đồ (ECG) và máy chụp X-quang cũng dựa vào các nguyên tắc của hiệu điện thế để hoạt động.

Hiệu điện thế không chỉ là một khái niệm lý thuyết mà còn có rất nhiều ứng dụng thực tiễn, đóng vai trò quan trọng trong nhiều lĩnh vực của đời sống và sản xuất.

Dưới đây là một số ví dụ về cách tính toán trong mạch điện khi đặt một hiệu điện thế \( U \) vào hai đầu mạch. Các ví dụ này sẽ giúp bạn hiểu rõ hơn về cách áp dụng các công thức cơ bản trong điện học.

1. Tính toán dòng điện qua điện trở

Giả sử ta có một mạch điện đơn giản bao gồm một điện trở \( R \) và một nguồn hiệu điện thế \( U \). Để tính dòng điện \( I \) chạy qua điện trở, ta áp dụng định luật Ohm:

\[
I = \frac{U}{R}
\]

Ví dụ, nếu \( U = 12V \) và \( R = 4\Omega \), dòng điện chạy qua điện trở sẽ là:

\[
I = \frac{12V}{4\Omega} = 3A
\]

2. Tính công suất tiêu thụ của mạch điện

Tiếp tục với ví dụ trên, công suất \( P \) tiêu thụ bởi điện trở có thể được tính bằng công thức:

\[
P = U \cdot I = I^2 \cdot R = \frac{U^2}{R}
\]

Với \( I = 3A \) và \( U = 12V \), ta có:

\[
P = 12V \cdot 3A = 36W
\]

Hoặc sử dụng công thức khác:

\[
P = \frac{(12V)^2}{4\Omega} = 36W
\]

3. Tính toán tổng trở trong mạch RLC

Xét một mạch RLC nối tiếp có các giá trị \( R = 10\Omega \), \( L = 0.1H \), và \( C = 100\mu F \). Hiệu điện thế \( U = 50V \) được đặt vào mạch với tần số \( f = 50Hz \). Ta cần tính tổng trở \( Z \) và dòng điện \( I \) trong mạch.

Đầu tiên, tính cảm kháng \( X_L \) và dung kháng \( X_C \):

\[
X_L = 2\pi f L = 2\pi \cdot 50 \cdot 0.1 = 31.42\Omega
\]

\[
X_C = \frac{1}{2\pi f C} = \frac{1}{2\pi \cdot 50 \cdot 100 \times 10^{-6}} = 31.83\Omega
\]

Tổng trở \( Z \) của mạch là:

\[
Z = \sqrt{R^2 + (X_L - X_C)^2} = \sqrt{10^2 + (31.42 - 31.83)^2} \approx 10.05\Omega
\]

Cuối cùng, tính dòng điện \( I \):

\[
I = \frac{U}{Z} = \frac{50V}{10.05\Omega} \approx 4.98A
\]

Với những ví dụ này, bạn có thể áp dụng vào các mạch điện thực tế để tính toán dòng điện, công suất, và tổng trở một cách chính xác.