Chủ đề điện trường tổng hợp bằng 0: Khám phá khái niệm "Điện Trường Tổng Hợp Bằng 0" trong vật lý, từ các định nghĩa cơ bản đến ứng dụng thực tiễn trong công nghệ và y học. Bài viết cũng bao gồm các bài tập minh họa chi tiết, giúp bạn hiểu rõ hơn về cách tính toán và ứng dụng khái niệm này trong các tình huống thực tế.
Mục lục
Cường độ Điện Trường Tổng Hợp Bằng 0
Trong lĩnh vực vật lý, đặc biệt là điện học, khái niệm "cường độ điện trường tổng hợp bằng 0" xuất hiện khi tại một điểm nào đó, tổng hợp các vectơ cường độ điện trường từ các nguồn điện tích khác nhau triệt tiêu lẫn nhau. Điều này có thể xảy ra trong nhiều tình huống khác nhau, từ bài toán lý thuyết cho đến các ứng dụng thực tiễn trong các lĩnh vực như điện hóa, y học, và công nghệ.
Khái Niệm và Định Nghĩa
Cường độ điện trường tại một điểm do một điện tích điểm tạo ra được xác định bởi công thức:
\[ E = \dfrac{k \cdot |q|}{r^2} \]
Với:
- E: Cường độ điện trường (V/m)
- k: Hằng số Coulomb \((k \approx 9 \times 10^9 \, \text{Nm}^2/\text{C}^2)\)
- q: Độ lớn của điện tích (C)
- r: Khoảng cách từ điện tích đến điểm cần tính (m)
Tại một điểm, nếu tổng hợp các cường độ điện trường do các điện tích khác nhau gây ra triệt tiêu lẫn nhau, thì cường độ điện trường tổng hợp tại đó bằng 0.
Ứng Dụng trong Thực Tế
- Trong Điện Hóa: Khi cường độ điện trường tổng hợp bằng 0, quá trình tạo màng trên bề mặt kim loại qua phản ứng điện hóa diễn ra ổn định, giúp cải thiện hiệu suất và chất lượng.
- Trong Y Học: Xác định vị trí cường độ điện trường bằng 0 giúp tối ưu hóa độ an toàn và độ chính xác trong các thiết bị y tế như máy xạ trị hay máy CT.
- Trong Công Nghệ: Việc điều chỉnh và kiểm soát cường độ điện trường trong các hệ thống viễn thông và công nghệ không dây giúp tối ưu hóa hiệu năng hoạt động của các thiết bị.
Bài Tập Minh Họa
- Bài Tập 1: Hai điện tích q1 = -12 × 10-6 C và q2 = 2.5 × 10-6 C đặt tại hai điểm A và B cách nhau 15 cm trong không khí. Tìm điểm M mà tại đó cường độ điện trường tổng hợp bằng 0.
- Bài Tập 2: Tại hai điểm A và B cách nhau 20 cm trong không khí, đặt hai điện tích q1 = -9 × 10-6 C và q2 = -4 × 10-6 C. Xác định vị trí điểm M mà tại đó cường độ điện trường tổng hợp bằng 0.
Phương Pháp Giải Quyết
Để tìm vị trí cường độ điện trường tổng hợp bằng 0, chúng ta cần đảm bảo rằng:
- Các vectơ cường độ điện trường phải cùng phương, ngược chiều và bằng nhau về độ lớn.
- Điểm M cần nằm trên đường nối giữa các điện tích, có thể nằm ngoài hoặc trong đoạn thẳng nối hai điện tích phụ thuộc vào dấu và độ lớn của các điện tích.
Ví dụ, với hai điện tích cùng dấu, điểm M thường nằm ngoài đoạn nối hai điện tích. Ngược lại, nếu hai điện tích trái dấu, điểm M thường nằm giữa hai điện tích.

.png)
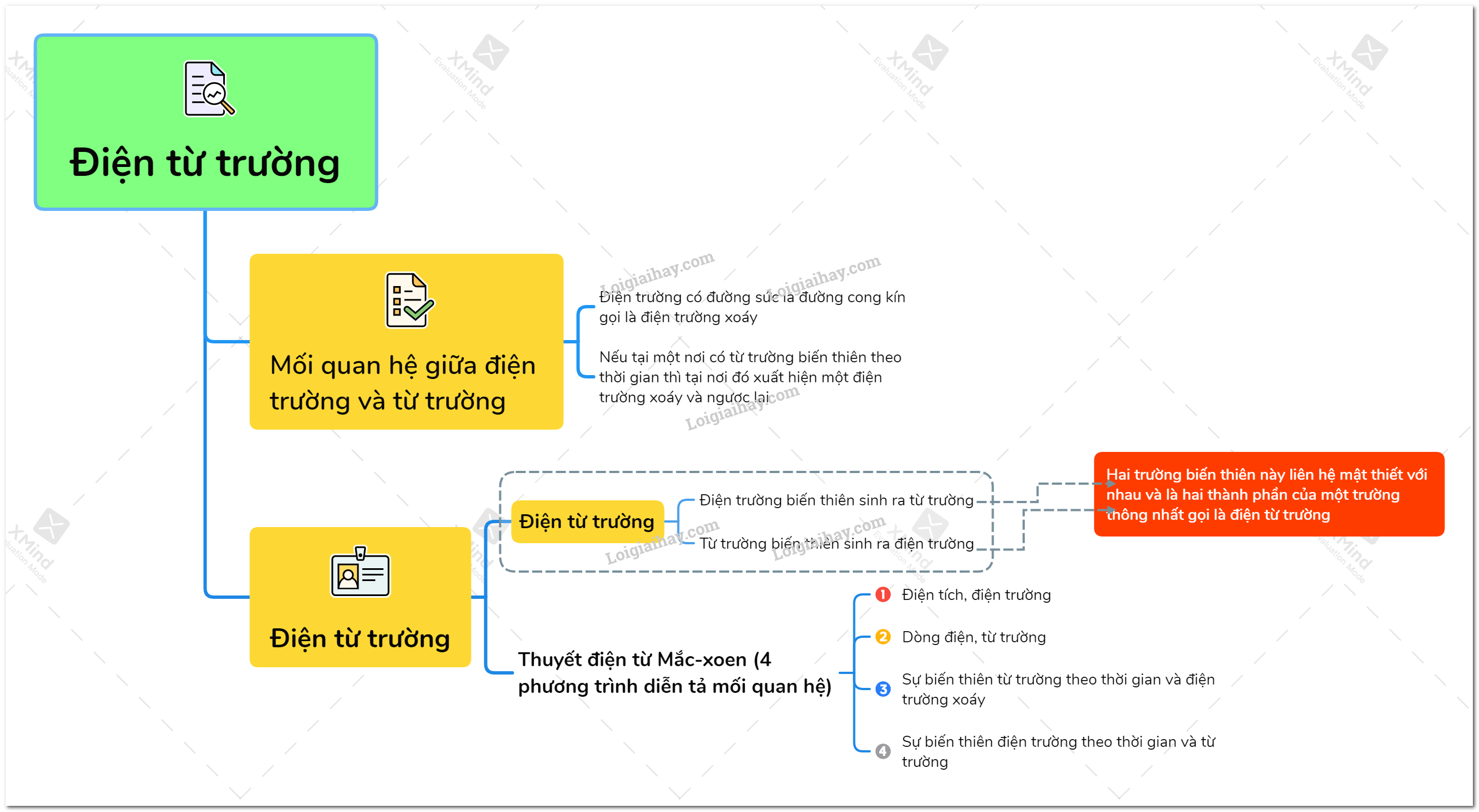
1. Khái Niệm Điện Trường và Điện Trường Tổng Hợp
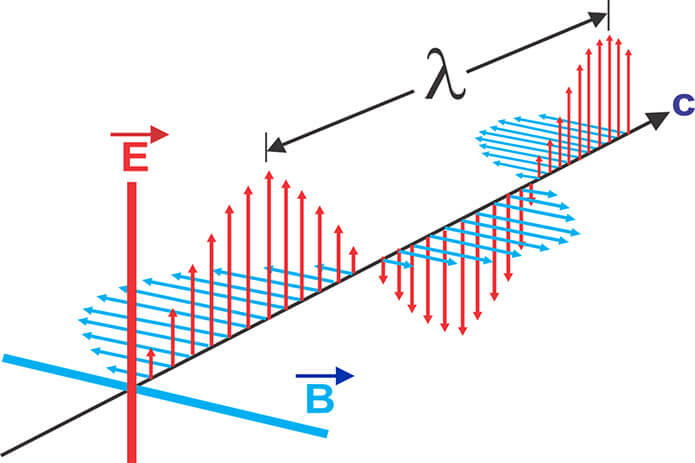
Điện trường là một khái niệm cơ bản trong vật lý, đại diện cho không gian xung quanh một điện tích mà tại đó, một điện tích khác sẽ chịu tác dụng của lực điện. Điện trường tại một điểm được biểu diễn bằng vectơ cường độ điện trường \( \vec{E} \), có phương và chiều trùng với lực tác dụng lên một điện tích dương đặt tại điểm đó. Công thức tính cường độ điện trường do một điện tích điểm gây ra là:
\[
E = \dfrac{k \cdot |q|}{r^2}
\]
Trong đó:
- \( E \): Cường độ điện trường tại điểm cần tính (V/m).
- \( k \): Hằng số Coulomb \(\left(k \approx 9 \times 10^9 \, \text{Nm}^2/\text{C}^2\right)\).
- \( q \): Điện tích của nguồn (C).
- \( r \): Khoảng cách từ điện tích đến điểm cần tính (m).
Điện trường tổng hợp là sự kết hợp của nhiều điện trường do các điện tích khác nhau tạo ra tại một điểm. Để tính điện trường tổng hợp tại một điểm, ta cần tính tổng các vectơ cường độ điện trường từ các điện tích đó. Điều này có thể được diễn tả bằng công thức:
\[
\vec{E}_{\text{tổng hợp}} = \vec{E}_1 + \vec{E}_2 + \dots + \vec{E}_n
\]
Trong trường hợp đặc biệt, khi các vectơ cường độ điện trường triệt tiêu lẫn nhau, tức là tổng hợp của chúng bằng 0, ta nói rằng tại điểm đó, điện trường tổng hợp bằng 0. Đây là một khái niệm quan trọng trong nhiều bài toán vật lý, đặc biệt là trong việc xác định vị trí cân bằng của các điện tích trong không gian.
2. Các Tình Huống Điện Trường Tổng Hợp Bằng 0
Có nhiều tình huống trong đó điện trường tổng hợp bằng 0 xuất hiện, đặc biệt là trong các bài toán vật lý liên quan đến sự tương tác của nhiều điện tích. Dưới đây là một số tình huống phổ biến và cách xác định vị trí điện trường tổng hợp bằng 0 trong từng trường hợp.
2.1. Điện Trường Tổng Hợp Bằng 0 Giữa Hai Điện Tích Cùng Dấu
Khi hai điện tích cùng dấu \( q_1 \) và \( q_2 \) đặt tại hai điểm cố định trong không gian, có một điểm nằm giữa chúng hoặc nằm ngoài khoảng giữa hai điện tích mà tại đó cường độ điện trường tổng hợp bằng 0. Điểm này thường nằm gần điện tích có giá trị nhỏ hơn. Để xác định vị trí này, ta sử dụng công thức:
\[
\vec{E}_1 + \vec{E}_2 = 0
\]
Nghĩa là, độ lớn của cường độ điện trường do \( q_1 \) gây ra phải bằng với độ lớn của cường độ điện trường do \( q_2 \) gây ra, nhưng có phương ngược chiều:
\[
\dfrac{k \cdot |q_1|}{r_1^2} = \dfrac{k \cdot |q_2|}{r_2^2}
\]
Trong đó, \( r_1 \) và \( r_2 \) là khoảng cách từ điểm cần tìm đến \( q_1 \) và \( q_2 \).
2.2. Điện Trường Tổng Hợp Bằng 0 Giữa Hai Điện Tích Trái Dấu
Với hai điện tích trái dấu \( q_1 \) và \( q_2 \), điểm mà tại đó điện trường tổng hợp bằng 0 thường nằm ngoài đoạn nối giữa hai điện tích, phía gần với điện tích có giá trị lớn hơn. Công thức tương tự được áp dụng:
\[
\vec{E}_1 + \vec{E}_2 = 0
\]
Công thức trên cho phép xác định vị trí điểm mà tổng cường độ điện trường do hai điện tích gây ra bằng 0:
\[
\dfrac{k \cdot |q_1|}{r_1^2} = \dfrac{k \cdot |q_2|}{r_2^2}
\]
2.3. Điện Trường Tổng Hợp Bằng 0 Trong Hệ Nhiều Điện Tích
Khi xét hệ gồm nhiều điện tích, việc xác định vị trí điện trường tổng hợp bằng 0 trở nên phức tạp hơn. Trong trường hợp này, ta cần tính toán tổng các vectơ cường độ điện trường do tất cả các điện tích trong hệ gây ra tại một điểm:
\[
\vec{E}_{\text{tổng hợp}} = \vec{E}_1 + \vec{E}_2 + \dots + \vec{E}_n = 0
\]
Vị trí của điểm mà tại đó cường độ điện trường tổng hợp bằng 0 phụ thuộc vào giá trị, vị trí của các điện tích trong không gian và hướng của các vectơ cường độ điện trường. Phương pháp này thường yêu cầu giải hệ phương trình hoặc sử dụng các kỹ thuật số để xác định chính xác vị trí.

3. Ứng Dụng Của Khái Niệm Điện Trường Tổng Hợp Bằng 0
Khái niệm điện trường tổng hợp bằng 0 có nhiều ứng dụng quan trọng trong cả lý thuyết và thực tiễn. Các ứng dụng này xuất hiện trong nhiều lĩnh vực khác nhau, từ công nghệ điện tử, viễn thông đến y học và nghiên cứu khoa học. Dưới đây là một số ứng dụng tiêu biểu của khái niệm này.
3.1. Ứng Dụng Trong Công Nghệ Điện Tử và Vật Liệu
Trong các mạch điện tử, việc điều chỉnh điện trường tổng hợp bằng 0 tại một số điểm có thể giúp kiểm soát tốt hơn các linh kiện điện tử nhạy cảm. Điều này có thể làm giảm nhiễu, tăng cường độ chính xác và độ bền của các thiết bị.
- Trong vật liệu bán dẫn, sự phân bố điện trường có ảnh hưởng lớn đến hiệu suất của các linh kiện như transistor và diode.
- Việc tạo ra các vùng có điện trường tổng hợp bằng 0 trong cấu trúc của vật liệu có thể cải thiện hiệu năng và độ tin cậy của các thiết bị.
3.2. Ứng Dụng Trong Y Học
Trong y học, đặc biệt là trong kỹ thuật hình ảnh và xạ trị, việc xác định và điều chỉnh điện trường tổng hợp là rất quan trọng. Điện trường tổng hợp bằng 0 có thể giúp tối ưu hóa việc phân bố liều lượng xạ trị, giảm thiểu tác động không mong muốn lên các mô khỏe mạnh.
- Máy chụp cộng hưởng từ (MRI) và các thiết bị y học khác sử dụng điện trường để tạo ra hình ảnh chi tiết của cơ thể. Việc kiểm soát điện trường tổng hợp giúp cải thiện độ chính xác của hình ảnh.
- Trong xạ trị, xác định điểm có điện trường tổng hợp bằng 0 giúp định hướng tia xạ chính xác hơn, bảo vệ các mô lành lân cận.
3.3. Ứng Dụng Trong Viễn Thông và Công Nghệ Không Dây
Trong lĩnh vực viễn thông, việc sử dụng khái niệm điện trường tổng hợp bằng 0 giúp cải thiện chất lượng tín hiệu và giảm nhiễu trong các hệ thống truyền thông không dây. Các kỹ thuật này thường được áp dụng trong thiết kế ăng-ten và mạng truyền thông.
- Thiết kế ăng-ten: Bằng cách điều chỉnh các phần tử ăng-ten sao cho điện trường tổng hợp tại một số vị trí bằng 0, ta có thể giảm thiểu nhiễu và tăng cường hướng tính của tín hiệu.
- Trong mạng truyền thông không dây, việc quản lý các vùng có điện trường tổng hợp bằng 0 giúp tối ưu hóa hiệu suất mạng và tăng cường chất lượng dịch vụ.
XEM THÊM:
4. Bài Tập và Phương Pháp Giải Quyết
Việc giải các bài tập liên quan đến điện trường tổng hợp bằng 0 giúp củng cố kiến thức và hiểu rõ hơn về các nguyên tắc cơ bản của điện học. Dưới đây là một số bài tập điển hình và phương pháp giải quyết từng bước để tìm ra vị trí điện trường tổng hợp bằng 0.
4.1. Bài Tập Điện Trường Tổng Hợp Bằng 0 Giữa Hai Điện Tích
Bài tập: Hai điện tích \( q_1 \) và \( q_2 \) đặt tại hai điểm A và B trong không gian. Hãy xác định vị trí trên đường thẳng AB mà tại đó điện trường tổng hợp bằng 0.
Phương pháp giải:
- Bước 1: Xác định hướng của các vectơ điện trường do \( q_1 \) và \( q_2 \) gây ra tại một điểm bất kỳ trên đường thẳng AB.
- Bước 2: Gọi \( x \) là khoảng cách từ điểm cần tìm đến điện tích \( q_1 \). Từ đó, khoảng cách đến \( q_2 \) sẽ là \( |AB| - x \).
- Bước 3: Viết biểu thức cường độ điện trường tại điểm cần tìm do \( q_1 \) và \( q_2 \) gây ra:
- Bước 4: Thiết lập phương trình cân bằng điện trường tổng hợp bằng cách đặt \( E_1 = E_2 \):
- Bước 5: Giải phương trình trên để tìm giá trị của \( x \), từ đó xác định vị trí của điểm cần tìm.
\[
E_1 = \dfrac{k \cdot |q_1|}{x^2}, \quad E_2 = \dfrac{k \cdot |q_2|}{(|AB| - x)^2}
\]
\[
\dfrac{k \cdot |q_1|}{x^2} = \dfrac{k \cdot |q_2|}{(|AB| - x)^2}
\]
4.2. Bài Tập Điện Trường Tổng Hợp Bằng 0 Trong Hệ Nhiều Điện Tích
Bài tập: Xét một hệ gồm ba điện tích \( q_1 \), \( q_2 \), và \( q_3 \) đặt tại các điểm A, B, và C trên cùng một mặt phẳng. Xác định vị trí trên mặt phẳng mà tại đó điện trường tổng hợp bằng 0.
Phương pháp giải:
- Bước 1: Tính cường độ điện trường do từng điện tích gây ra tại một điểm bất kỳ trên mặt phẳng.
- Bước 2: Thiết lập phương trình cho tổng hợp vectơ điện trường tại điểm cần tìm bằng 0:
- Bước 3: Giải hệ phương trình để tìm tọa độ của điểm mà tại đó tổng hợp điện trường bằng 0.
- Bước 4: Xác minh kết quả bằng cách tính toán lại các cường độ điện trường tại điểm vừa tìm được.
\[
\vec{E}_1 + \vec{E}_2 + \vec{E}_3 = 0
\]
4.3. Phương Pháp Giải Quyết và Các Lưu Ý
Khi giải các bài tập liên quan đến điện trường tổng hợp bằng 0, điều quan trọng là phải xác định đúng hướng của các vectơ cường độ điện trường và cẩn thận trong việc thiết lập các phương trình. Một số lưu ý cần nhớ:
- Sử dụng hệ tọa độ thích hợp để đơn giản hóa các phép tính.
- Luôn kiểm tra lại kết quả bằng cách thay vào các phương trình ban đầu.
- Nếu bài toán phức tạp, hãy vẽ hình minh họa để trực quan hóa vấn đề.