Chủ đề điện trở tương đương ký hiệu là gì: Điện trở tương đương ký hiệu là gì? Bài viết này sẽ giải đáp mọi thắc mắc về khái niệm, ký hiệu và cách tính toán điện trở tương đương trong các mạch điện. Tìm hiểu cách áp dụng kiến thức này trong thực tiễn để tối ưu hóa thiết kế và phân tích mạch điện, đảm bảo hiệu suất và an toàn.
Mục lục
- Điện Trở Tương Đương và Ký Hiệu Trong Mạch Điện
- 1. Khái Niệm Về Điện Trở Tương Đương
- 2. Ký Hiệu Và Công Thức Tính Điện Trở Tương Đương
- 3. Các Phương Pháp Tính Toán Điện Trở Tương Đương
- 4. Ứng Dụng Của Điện Trở Tương Đương
- 5. Các Lỗi Thường Gặp Khi Tính Điện Trở Tương Đương
- 6. Các Ví Dụ Minh Họa Cụ Thể Về Điện Trở Tương Đương
Điện Trở Tương Đương và Ký Hiệu Trong Mạch Điện
Điện trở tương đương là một khái niệm quan trọng trong lĩnh vực điện học. Nó đại diện cho tổng trở của một hệ thống các điện trở khi chúng được kết nối theo các cấu hình khác nhau như nối tiếp, song song hoặc hỗn hợp. Khi tính toán điện trở tương đương, ta có thể đơn giản hóa mạch điện phức tạp thành một điện trở duy nhất.
Ký Hiệu và Công Thức Tính Điện Trở Tương Đương
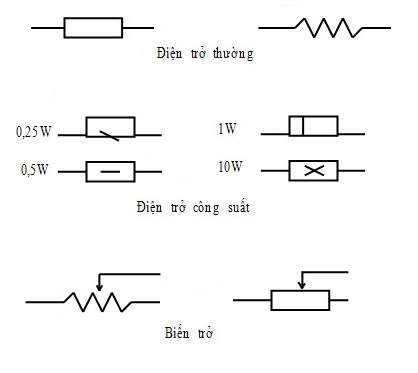
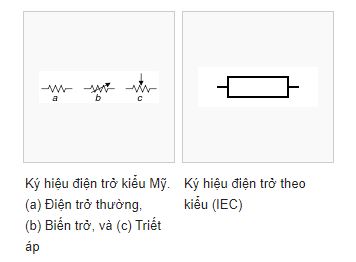
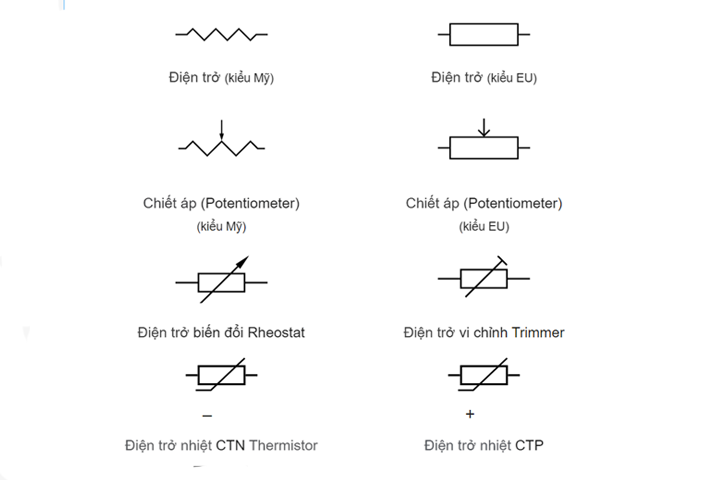
Điện trở tương đương thường được ký hiệu là Rtđ trong các tài liệu kỹ thuật và sách giáo khoa. Công thức tính điện trở tương đương khác nhau tùy thuộc vào cách kết nối các điện trở:
- Điện trở nối tiếp: Tổng điện trở tương đương là tổng của tất cả các điện trở thành phần:
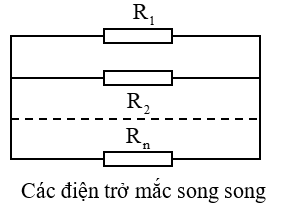
- Điện trở song song: Điện trở tương đương được tính bằng công thức nghịch đảo của tổng nghịch đảo các điện trở:
- Điện trở hỗn hợp: Đối với mạch hỗn hợp, ta cần tách mạch ra từng phần nhỏ và áp dụng các công thức trên một cách tuần tự để tính toán.
$$R_{tđ} = R_1 + R_2 + R_3 + \dots + R_n$$
$$\frac{1}{R_{tđ}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \dots + \frac{1}{R_n}$$
Ứng Dụng Của Điện Trở Tương Đương
Việc tính toán điện trở tương đương giúp đơn giản hóa việc phân tích mạch điện, từ đó dễ dàng xác định được cường độ dòng điện, hiệu điện thế trong các phần khác nhau của mạch. Điều này đặc biệt quan trọng trong thiết kế và sửa chữa các thiết bị điện tử.
Bảng Ví Dụ Tính Điện Trở Tương Đương
| Cấu Hình Kết Nối | Công Thức Tính | Ví Dụ Tính Toán |
| Nối tiếp | $$R_{tđ} = R_1 + R_2 + R_3$$ | $$R_{tđ} = 2\Omega + 3\Omega + 5\Omega = 10\Omega$$ |
| Song song | $$\frac{1}{R_{tđ}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}$$ | $$\frac{1}{R_{tđ}} = \frac{1}{4\Omega} + \frac{1}{6\Omega} = 2.4\Omega$$ |
| Hỗn hợp | Kết hợp các công thức trên | Thực hiện tuần tự các phép tính nối tiếp và song song |
Kết Luận
Điện trở tương đương là một khái niệm cơ bản nhưng rất quan trọng trong kỹ thuật điện. Nắm vững cách tính toán và ứng dụng điện trở tương đương sẽ giúp bạn tối ưu hóa hiệu suất của các mạch điện và thiết bị điện tử.
.png)
1. Khái Niệm Về Điện Trở Tương Đương
Điện trở tương đương là một khái niệm quan trọng trong điện học, dùng để biểu thị tổng trở của một hệ thống nhiều điện trở khi chúng được kết nối theo các cách khác nhau trong mạch điện. Khái niệm này giúp đơn giản hóa mạch điện phức tạp thành một điện trở duy nhất, giúp dễ dàng tính toán và phân tích.
Cụ thể, điện trở tương đương có thể được hiểu là điện trở mà nếu đặt vào cùng một vị trí trong mạch, sẽ tạo ra cùng một mức dòng điện như toàn bộ các điện trở thực sự trong mạch.
- Nối tiếp: Khi các điện trở được nối tiếp, điện trở tương đương là tổng các điện trở thành phần:
- Song song: Khi các điện trở được mắc song song, điện trở tương đương được tính bằng công thức nghịch đảo của tổng nghịch đảo các điện trở:
- Mạch hỗn hợp: Trong trường hợp mạch hỗn hợp, ta cần phân tích mạch thành các phần nhỏ hơn và tính toán tuần tự theo các quy tắc trên.
$$R_{tđ} = R_1 + R_2 + R_3 + \dots + R_n$$
$$\frac{1}{R_{tđ}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \dots + \frac{1}{R_n}$$
Khái niệm điện trở tương đương không chỉ hữu ích trong việc tính toán các thông số điện mà còn đóng vai trò quan trọng trong thiết kế và phân tích các hệ thống điện phức tạp. Nó giúp các kỹ sư và nhà nghiên cứu có thể tối ưu hóa và đơn giản hóa quá trình làm việc với mạch điện.
2. Ký Hiệu Và Công Thức Tính Điện Trở Tương Đương
Trong lĩnh vực điện học, ký hiệu của điện trở tương đương thường được biểu thị bằng Rtđ hoặc Req. Ký hiệu này đại diện cho tổng trở của một hệ thống nhiều điện trở khi chúng được kết nối với nhau theo các cách khác nhau như nối tiếp, song song hoặc hỗn hợp.
Ký Hiệu Điện Trở Tương Đương
- Rtđ: Ký hiệu thường dùng trong sách giáo khoa và tài liệu kỹ thuật ở Việt Nam.
- Req: Ký hiệu phổ biến trong các tài liệu quốc tế, viết tắt của "Equivalent Resistance".
Công Thức Tính Điện Trở Tương Đương
Điện trở tương đương có thể được tính toán dựa trên cách các điện trở thành phần được kết nối trong mạch:
- Điện trở nối tiếp: Khi các điện trở được nối tiếp nhau, điện trở tương đương được tính bằng tổng các điện trở thành phần:
- Điện trở song song: Khi các điện trở được mắc song song, điện trở tương đương được tính bằng công thức nghịch đảo của tổng nghịch đảo các điện trở:
- Mạch hỗn hợp: Đối với mạch hỗn hợp, việc tính toán điện trở tương đương sẽ phức tạp hơn, cần phân tích mạch thành các phần nối tiếp và song song rồi áp dụng các công thức tương ứng để tính toán:
$$R_{tđ} = R_1 + R_2 + R_3 + \dots + R_n$$
$$\frac{1}{R_{tđ}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \dots + \frac{1}{R_n}$$
Các công thức trên giúp đơn giản hóa việc phân tích và thiết kế mạch điện, đảm bảo các yếu tố về hiệu quả và an toàn trong quá trình vận hành. Việc hiểu rõ và áp dụng chính xác các công thức này là nền tảng quan trọng cho những ai làm việc trong lĩnh vực điện tử và kỹ thuật điện.

3. Các Phương Pháp Tính Toán Điện Trở Tương Đương
Việc tính toán điện trở tương đương là một phần quan trọng trong phân tích và thiết kế mạch điện. Có nhiều phương pháp khác nhau để thực hiện tính toán này, tùy thuộc vào cấu hình của mạch điện. Dưới đây là các phương pháp cơ bản mà bạn có thể sử dụng.
3.1. Phương Pháp Tính Thủ Công
Phương pháp tính thủ công là phương pháp cơ bản và thường được sử dụng nhất. Với phương pháp này, ta tính toán từng bước dựa trên các quy tắc kết nối của điện trở:
- Nối tiếp: Điện trở tương đương của các điện trở nối tiếp bằng tổng các điện trở thành phần.
- Song song: Điện trở tương đương của các điện trở song song được tính bằng nghịch đảo của tổng nghịch đảo các điện trở thành phần.
- Mạch hỗn hợp: Đối với mạch hỗn hợp, ta phải phân tích mạch thành các phần nối tiếp và song song riêng biệt, sau đó áp dụng các công thức tương ứng để tính toán điện trở tương đương từng phần trước khi ghép lại.
$$R_{tđ} = R_1 + R_2 + R_3 + \dots + R_n$$
$$\frac{1}{R_{tđ}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \dots + \frac{1}{R_n}$$
3.2. Sử Dụng Công Cụ Phần Mềm Để Tính Toán
Với sự phát triển của công nghệ, việc tính toán điện trở tương đương có thể được thực hiện nhanh chóng và chính xác hơn bằng cách sử dụng các công cụ phần mềm chuyên dụng. Một số công cụ phổ biến như:
- SPICE: Đây là một phần mềm mô phỏng mạch điện mạnh mẽ, giúp mô phỏng và tính toán điện trở tương đương trong các mạch điện phức tạp.
- Các công cụ tính toán trực tuyến: Nhiều trang web cung cấp công cụ tính toán điện trở tương đương đơn giản, cho phép nhập các giá trị điện trở và cấu hình mạch để tính toán kết quả nhanh chóng.
- Phần mềm vẽ mạch điện: Các phần mềm như Proteus, Multisim cũng tích hợp khả năng tính toán điện trở tương đương khi bạn xây dựng mô hình mạch trên chúng.
3.3. Phân Tích Sử Dụng Định Luật Ohm và Định Lý Kirchhoff
Trong một số trường hợp phức tạp hơn, bạn có thể cần sử dụng định luật Ohm và định lý Kirchhoff để phân tích và tính toán điện trở tương đương. Phương pháp này thường được áp dụng khi các điện trở không chỉ nối tiếp hoặc song song đơn giản mà kết hợp với các nguồn điện khác nhau:
- Định luật Ohm: Giúp tính toán mối quan hệ giữa điện áp, dòng điện và điện trở trong mạch.
- Định lý Kirchhoff: Định lý về điện áp và dòng điện trong mạch, cho phép tính toán điện trở tương đương trong các mạch phức tạp bằng cách áp dụng các quy tắc về bảo toàn điện áp và dòng điện.
Nhờ vào các phương pháp tính toán này, bạn có thể dễ dàng xác định điện trở tương đương trong các mạch điện khác nhau, giúp đơn giản hóa quá trình thiết kế và phân tích mạch.
XEM THÊM:
4. Ứng Dụng Của Điện Trở Tương Đương
Điện trở tương đương là một khái niệm quan trọng được ứng dụng rộng rãi trong nhiều lĩnh vực của kỹ thuật điện và điện tử. Hiểu rõ và áp dụng đúng cách điện trở tương đương giúp tối ưu hóa các thiết kế mạch điện, đảm bảo an toàn và hiệu quả trong nhiều ứng dụng thực tiễn. Dưới đây là một số ứng dụng phổ biến của điện trở tương đương:
- Thiết kế và phân tích mạch điện: Điện trở tương đương giúp đơn giản hóa các mạch điện phức tạp, cho phép kỹ sư nhanh chóng tính toán và phân tích các đặc tính mạch như điện áp, dòng điện, và công suất.
- Ứng dụng trong mạch phân áp: Trong các mạch phân áp, điện trở tương đương được sử dụng để điều chỉnh và phân chia điện áp giữa các thành phần của mạch. Điều này rất quan trọng trong việc cung cấp điện áp thích hợp cho các thiết bị điện tử.
- Thiết kế mạch lọc và mạch khuếch đại: Điện trở tương đương đóng vai trò quan trọng trong việc xác định các đặc tính tần số của mạch lọc và mạch khuếch đại. Bằng cách tính toán điện trở tương đương, kỹ sư có thể thiết kế các mạch với đặc tính tần số mong muốn.
- Bảo vệ mạch điện: Điện trở tương đương có thể được sử dụng để bảo vệ mạch khỏi quá dòng hoặc quá áp. Bằng cách thêm các điện trở trong các vị trí chiến lược, điện trở tương đương có thể giúp hạn chế dòng điện hoặc giảm điện áp xuống mức an toàn.
- Điều chỉnh và kiểm soát nhiệt độ: Trong các ứng dụng nhiệt, điện trở tương đương được sử dụng để điều chỉnh và kiểm soát nhiệt độ của các thiết bị điện tử. Bằng cách thay đổi giá trị điện trở, có thể kiểm soát lượng nhiệt sinh ra trong mạch.
Nhìn chung, điện trở tương đương không chỉ là một công cụ lý thuyết mà còn có những ứng dụng thiết thực trong việc nâng cao hiệu suất và độ tin cậy của các hệ thống điện và điện tử. Việc hiểu rõ và áp dụng đúng cách điện trở tương đương là một kỹ năng quan trọng đối với các kỹ sư và nhà thiết kế trong lĩnh vực này.

5. Các Lỗi Thường Gặp Khi Tính Điện Trở Tương Đương
Trong quá trình tính toán điện trở tương đương, người học thường gặp phải một số lỗi phổ biến. Những lỗi này có thể dẫn đến sai sót trong việc xác định giá trị điện trở, gây ảnh hưởng đến hiệu suất của mạch điện. Dưới đây là một số lỗi thường gặp và cách khắc phục:
5.1. Lỗi Khi Nhận Diện Các Mạch Nối Tiếp và Song Song
Một trong những lỗi phổ biến nhất là nhầm lẫn giữa mạch nối tiếp và mạch song song. Điều này thường xảy ra khi mạch có cấu trúc phức tạp:
- Mạch nối tiếp: Các điện trở được mắc nối tiếp khi chúng nằm trên cùng một đường dẫn dòng điện. Tổng điện trở tương đương là tổng các điện trở thành phần.
- Mạch song song: Các điện trở mắc song song khi chúng có hai đầu nối chung với nhau. Điện trở tương đương được tính bằng công thức nghịch đảo của tổng các nghịch đảo điện trở thành phần.
5.2. Lỗi Tính Toán Trong Mạch Hỗn Hợp
Mạch hỗn hợp kết hợp cả nối tiếp và song song, thường gây khó khăn cho việc tính toán. Nếu không phân tích đúng cấu trúc mạch, rất dễ dẫn đến sai sót:
- Xác định từng phần của mạch là nối tiếp hay song song.
- Tính toán điện trở tương đương cho từng phần nhỏ trước khi gộp lại toàn mạch.
5.3. Lỗi Sử Dụng Sai Công Thức
Nhiều người học có thể sử dụng nhầm công thức khi tính toán điện trở tương đương, đặc biệt là trong các mạch phức tạp. Điều này thường xảy ra khi:
- Nhầm lẫn giữa công thức của mạch nối tiếp và song song.
- Không chú ý đến các đơn vị của điện trở, dẫn đến sai sót trong tính toán.
5.4. Bỏ Qua Các Yếu Tố Ảnh Hưởng Khác
Khi tính toán điện trở tương đương, không chỉ có các điện trở thành phần mà còn có các yếu tố khác ảnh hưởng đến kết quả, chẳng hạn như:
- Điện trở tiếp xúc tại các điểm nối.
- Sự thay đổi nhiệt độ ảnh hưởng đến giá trị điện trở.
- Điện cảm và điện dung trong mạch có thể gây nhiễu đến phép tính.
5.5. Lỗi Khi Áp Dụng Các Định Luật Và Định Lý
Khi áp dụng định luật Ohm và định lý Kirchhoff trong các mạch phức tạp, người học có thể mắc lỗi do:
- Không đúng cách khi áp dụng định luật Ohm cho toàn mạch hoặc từng phần mạch.
- Sử dụng không đúng các phương trình của định lý Kirchhoff, dẫn đến kết quả sai lệch.
Để tránh các lỗi trên, việc kiểm tra lại từng bước trong quá trình tính toán và áp dụng đúng các công thức là rất quan trọng. Sự cẩn thận và chính xác trong từng phép tính sẽ giúp đảm bảo kết quả đúng đắn và hiệu quả cho hệ thống mạch điện.
6. Các Ví Dụ Minh Họa Cụ Thể Về Điện Trở Tương Đương
6.1. Ví Dụ Tính Toán Với Mạch Nối Tiếp
Giả sử chúng ta có một mạch điện đơn giản gồm 3 điện trở R1 = 4Ω, R2 = 6Ω và R3 = 8Ω được mắc nối tiếp.
- Điện trở tương đương của mạch được tính bằng công thức:
\( R_{td} = R_1 + R_2 + R_3 \)
\( R_{td} = 4Ω + 6Ω + 8Ω = 18Ω \) - Điện trở tương đương của mạch là 18Ω. Điều này có nghĩa là mạch điện có thể được thay thế bằng một điện trở duy nhất có giá trị 18Ω.
6.2. Ví Dụ Tính Toán Với Mạch Song Song
Trong trường hợp này, giả sử có 3 điện trở R1 = 3Ω, R2 = 6Ω và R3 = 9Ω mắc song song với nhau.
- Điện trở tương đương của mạch song song được tính bằng công thức:
\( \frac{1}{R_{td}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \)
\( \frac{1}{R_{td}} = \frac{1}{3Ω} + \frac{1}{6Ω} + \frac{1}{9Ω} \)
\( \frac{1}{R_{td}} = \frac{6}{18} + \frac{3}{18} + \frac{2}{18} = \frac{11}{18} \) - Suy ra:
\( R_{td} = \frac{18}{11}Ω \approx 1.64Ω \) - Điện trở tương đương của mạch là 1.64Ω.
6.3. Ví Dụ Tính Toán Với Mạch Hỗn Hợp
Giả sử mạch điện hỗn hợp gồm hai điện trở R1 = 10Ω và R2 = 20Ω mắc nối tiếp với một nhánh song song gồm hai điện trở R3 = 30Ω và R4 = 60Ω.
- Tính điện trở tương đương của nhánh song song:
\( \frac{1}{R_{song}} = \frac{1}{R_3} + \frac{1}{R_4} \)
\( \frac{1}{R_{song}} = \frac{1}{30Ω} + \frac{1}{60Ω} \)
\( \frac{1}{R_{song}} = \frac{3}{90} + \frac{1.5}{90} = \frac{4.5}{90} = \frac{1}{20Ω} \)
Suy ra:
\( R_{song} = 20Ω \) - Mạch hỗn hợp giờ đây trở thành mạch nối tiếp gồm ba điện trở: R1 = 10Ω, R2 = 20Ω, và Rsong = 20Ω.
Tính điện trở tương đương của mạch:
\( R_{td} = R_1 + R_2 + R_{song} \)
\( R_{td} = 10Ω + 20Ω + 20Ω = 50Ω \) - Điện trở tương đương của mạch là 50Ω.



.png)