Chủ đề diện tích parabol: Diện tích parabol là một chủ đề quan trọng trong toán học, đặc biệt hữu ích trong nhiều lĩnh vực khoa học và kỹ thuật. Bài viết này cung cấp công thức, phương pháp tính và những ứng dụng thực tiễn của diện tích parabol để giúp bạn hiểu rõ và áp dụng một cách hiệu quả.
Mục lục
Tính Diện Tích Hình Phẳng Giới Hạn Bởi Parabol
Diện tích của hình phẳng giới hạn bởi parabol và các đường khác có thể được tính bằng cách sử dụng tích phân. Dưới đây là các ví dụ cụ thể và công thức để tính diện tích này.
1. Diện Tích Giới Hạn Bởi Parabol Và Đường Thẳng
Xét parabol y = x^2 và đường thẳng y = 2x - 1. Để tìm diện tích giới hạn bởi parabol và đường thẳng này, ta thực hiện các bước sau:
\[
x^2 = 2x - 1 \\
\Rightarrow x^2 - 2x + 1 = 0 \\
\Rightarrow (x - 1)^2 = 0 \\
\Rightarrow x = 1
\]
\[
\int_{0}^{1} (2x - 1) \, dx = \left[ x^2 - x \right]_{0}^{1} = 0 \\
\int_{0}^{1} x^2 \, dx = \left[ \frac{x^3}{3} \right]_{0}^{1} = \frac{1}{3}
\]
\[
S = \int_{0}^{1} \left( (2x - 1) - x^2 \right) dx = \left[ x^2 - \frac{x^3}{3} \right]_{0}^{1} = \frac{2}{3}
\]
- Tìm giao điểm của hai đường bằng cách giải phương trình x^2 = 2x - 1:
- Xác định các điểm cắt: A(0, -1) và D(1, 1).
- Tính tích phân của các hàm số trên khoảng từ 0 đến 1:
- Tính diện tích bằng cách trừ các tích phân:
2. Diện Tích Giới Hạn Bởi Hai Parabol
Xét hai parabol y = x^2 và y = 2 - x^2. Để tính diện tích giữa hai parabol này, ta thực hiện các bước sau:
\[
x^2 = 2 - x^2 \\
\Rightarrow 2x^2 = 2 \\
\Rightarrow x^2 = 1 \\
\Rightarrow x = \pm 1
\]
\[
S = \int_{-1}^{1} \left( (2 - x^2) - x^2 \right) dx \\
= \int_{-1}^{1} (2 - 2x^2) \, dx
\]
- Tìm giao điểm của hai parabol bằng cách giải phương trình x^2 = 2 - x^2:
- Xác định các điểm cắt: (-1, 2) và (1, 2).
- Tính tích phân của hiệu các hàm số trên khoảng từ -1 đến 1:
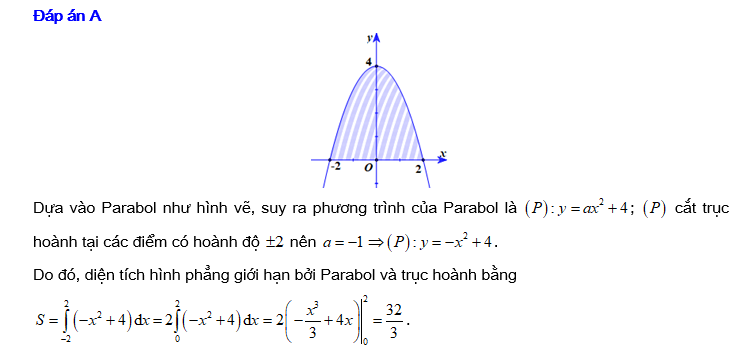
3. Công Thức Tính Nhanh Diện Tích Hình Phẳng Giới Hạn Bởi Parabol Và Trục Hoành
Cho parabol y = ax^2 + bx + c với b^2 - 4ac > 0. Khi đó, diện tích hình phẳng S được giới hạn bởi đồ thị của parabol và trục hoành được tính như sau:
\[
S = \int_{x_1}^{x_2} (ax^2 + bx + c) \, dx
\]
Với x_1, x_2 là hai nghiệm của phương trình ax^2 + bx + c = 0. Công thức tính diện tích nhanh là:
\[
S = \frac{(b^2 - 4ac)\sqrt{b^2 - 4ac}}{6a^2}
\]
4. Ví Dụ Tính Diện Tích Hình Phẳng
Tính diện tích hình phẳng giới hạn bởi parabol y = x^2 - 5x + 6 và trục hoành. Áp dụng công thức trên với a = 1, b = -5, c = 6, ta có:
\[
S = \frac{(b^2 - 4ac)\sqrt{b^2 - 4ac}}{6a^2} = \frac{(25 - 24)\sqrt{1}}{6} = \frac{1}{6}
\]

.png)
1. Giới thiệu về Parabol
Parabol là một hình dạng toán học đặc biệt được định nghĩa là tập hợp các điểm trong mặt phẳng sao cho khoảng cách từ mỗi điểm đến một điểm cố định (tiêu điểm) bằng khoảng cách từ điểm đó đến một đường thẳng cố định (đường chuẩn).
Phương trình tổng quát của một parabol trong hệ tọa độ Đề-các là:
\( y = ax^2 + bx + c \)
Trong đó:
- a là hệ số của \(x^2\), xác định độ mở của parabol.
- b là hệ số của \(x\), xác định độ dịch chuyển ngang.
- c là hằng số, xác định độ dịch chuyển dọc.
Để hiểu rõ hơn về cấu trúc của parabol, ta có thể phân tích các thành phần của nó như sau:
- Đỉnh (vertex): Đỉnh của parabol là điểm có tọa độ \(\left(-\frac{b}{2a}, c - \frac{b^2}{4a}\right)\).
- Tiêu điểm (focus): Tiêu điểm của parabol có tọa độ \(\left(-\frac{b}{2a}, c - \frac{b^2 - 1}{4a}\right)\).
- Đường chuẩn (directrix): Đường chuẩn của parabol có phương trình \(y = c - \frac{b^2 + 1}{4a}\).
Một số tính chất quan trọng của parabol:
- Parabol có trục đối xứng là đường thẳng đi qua đỉnh và vuông góc với đường chuẩn.
- Parabol có tính chất phản xạ: Tia sáng song song với trục đối xứng sau khi phản xạ tại parabol sẽ đi qua tiêu điểm.
Dưới đây là bảng mô tả các yếu tố chính của parabol:
| Thành phần | Công thức |
| Đỉnh | \(\left(-\frac{b}{2a}, c - \frac{b^2}{4a}\right)\) |
| Tiêu điểm | \(\left(-\frac{b}{2a}, c - \frac{b^2 - 1}{4a}\right)\) |
| Đường chuẩn | \(y = c - \frac{b^2 + 1}{4a}\) |
Parabol có nhiều ứng dụng trong thực tế như trong thiết kế anten parabol, đèn pha ô tô và các công trình kiến trúc.
2. Công thức tính diện tích hình phẳng giới hạn bởi Parabol
Diện tích hình phẳng giới hạn bởi một parabol và trục hoành hoặc các đường thẳng có thể được tính bằng cách sử dụng tích phân. Dưới đây là các bước cụ thể để tính diện tích này.
1. Diện tích hình phẳng giới hạn bởi parabol và trục hoành
Giả sử ta có parabol với phương trình:
\( y = ax^2 + bx + c \)
Và hai điểm giao của parabol với trục hoành là \( x_1 \) và \( x_2 \). Diện tích hình phẳng \( S \) giới hạn bởi parabol và trục hoành được tính bằng:
\( S = \int_{x_1}^{x_2} (ax^2 + bx + c) \, dx \)
Sử dụng tích phân cơ bản, ta có:
\( S = \int_{x_1}^{x_2} (ax^2 + bx + c) \, dx = \left[ \frac{a}{3}x^3 + \frac{b}{2}x^2 + cx \right]_{x_1}^{x_2} \)
Thay các giá trị \( x_1 \) và \( x_2 \) vào để tính diện tích cụ thể.
2. Diện tích hình phẳng giới hạn bởi parabol và đường thẳng
Giả sử ta có parabol với phương trình:
\( y_1 = ax^2 + bx + c \)
Và đường thẳng với phương trình:
\( y_2 = mx + n \)
Để tính diện tích hình phẳng giới hạn bởi parabol và đường thẳng, trước tiên ta cần tìm các điểm giao của chúng bằng cách giải phương trình:
\( ax^2 + (b - m)x + (c - n) = 0 \)
Giả sử các nghiệm của phương trình này là \( x_3 \) và \( x_4 \). Diện tích hình phẳng \( S \) được tính bằng:
\( S = \int_{x_3}^{x_4} |(ax^2 + bx + c) - (mx + n)| \, dx \)
Chia nhỏ biểu thức bên trong dấu giá trị tuyệt đối và tính tích phân từng phần:
\( S = \int_{x_3}^{x_4} |ax^2 + (b - m)x + (c - n)| \, dx \)
Sử dụng tích phân cơ bản, ta có:
\( S = \int_{x_3}^{x_4} (ax^2 + (b - m)x + (c - n)) \, dx = \left[ \frac{a}{3}x^3 + \frac{b - m}{2}x^2 + (c - n)x \right]_{x_3}^{x_4} \)
3. Ví dụ cụ thể
Giả sử ta có parabol:
\( y = x^2 - 4x + 3 \)
Và trục hoành. Ta tìm các điểm giao của parabol với trục hoành:
\( x^2 - 4x + 3 = 0 \)
Giải phương trình, ta được \( x_1 = 1 \) và \( x_2 = 3 \). Diện tích hình phẳng \( S \) được tính bằng:
\( S = \int_{1}^{3} (x^2 - 4x + 3) \, dx = \left[ \frac{1}{3}x^3 - 2x^2 + 3x \right]_{1}^{3} \)
Thay giá trị vào, ta được:
\( S = \left( \frac{1}{3}(3^3) - 2(3^2) + 3(3) \right) - \left( \frac{1}{3}(1^3) - 2(1^2) + 3(1) \right) = \left( 9 - 18 + 9 \right) - \left( \frac{1}{3} - 2 + 3 \right) = 0 - \left( \frac{1}{3} \right) = \frac{8}{3} \)

3. Phương pháp tính tích phân để tìm diện tích
Để tính diện tích hình phẳng giới hạn bởi parabol và các đường thẳng, ta sử dụng phương pháp tính tích phân. Các bước thực hiện cụ thể như sau:
- Xác định các hàm số giới hạn vùng cần tính diện tích, ví dụ parabol \( y = ax^2 + bx + c \) và đường thẳng \( y = mx + n \).
- Xác định các điểm giao của các hàm số này bằng cách giải phương trình \( ax^2 + bx + c = mx + n \).
- Chọn hệ trục tọa độ sao cho đỉnh parabol trùng với gốc tọa độ O hoặc nằm trên trục Oy để đơn giản hóa tính toán.
- Tính tích phân của hàm số hiệu giữa các giới hạn trong khoảng xác định:
Công thức tổng quát để tính diện tích \( S \) giữa hai đường cong \( y_1 = f(x) \) và \( y_2 = g(x) \) từ \( x = a \) đến \( x = b \) là:
\[
S = \int_{a}^{b} (f(x) - g(x)) \, dx
\]
Ví dụ, nếu \( y_1 = ax^2 + bx + c \) và \( y_2 = mx + n \), công thức tích phân sẽ là:
\[
S = \int_{x_1}^{x_2} \left( ax^2 + bx + c - (mx + n) \right) \, dx
\]
Trong đó, \( x_1 \) và \( x_2 \) là các nghiệm của phương trình \( ax^2 + bx + c = mx + n \).
- Nếu hàm số phức tạp, bạn có thể chia nhỏ tích phân thành nhiều phần và tính từng phần riêng biệt.
- Để đảm bảo tính chính xác, hãy kiểm tra lại kết quả bằng các phương pháp số hoặc phần mềm tính toán.
Áp dụng các bước trên sẽ giúp bạn tính được diện tích hình phẳng giới hạn bởi các đường cong một cách hiệu quả và chính xác.

XEM THÊM:
4. Ví dụ minh họa
Để minh họa cho công thức tính diện tích hình phẳng giới hạn bởi parabol, chúng ta sẽ xét ví dụ cụ thể với parabol y = x^2 - 6x + 12 và các đường thẳng y = m, x = 0, x = 1.
Giả sử chúng ta cần tính diện tích hình phẳng giới hạn bởi parabol y = x^2 - 6x + 12 và trục hoành từ x = 0 đến x = 1.
Ta có công thức tích phân để tính diện tích:
S [ 0 , 1 ] = ∫ 0 1 | x 2 - 6 x + 12 | d xTa tiến hành tính tích phân trên:
S = ∫ 0 1 | x 2 + 2 x + 1 | d xPhân tích kết quả tích phân:
Ta có:
S = x 3 + x 2 + x | [ 0 , 1 ] = 2 3Như vậy, diện tích hình phẳng giới hạn bởi parabol y = x^2 - 6x + 12 và các đường thẳng từ x = 0 đến x = 1 là \(\frac{2}{3}\) đơn vị diện tích.

5. Ứng dụng của Parabol trong thực tế
Parabol không chỉ là một khái niệm toán học, mà còn có nhiều ứng dụng thực tiễn trong đời sống. Dưới đây là một số ứng dụng của parabol:
- Gương parabol: Gương parabol được sử dụng trong các thiết bị quang học như kính thiên văn, ống nhòm, giúp tập trung ánh sáng vào một điểm tiêu duy nhất, tạo ra hình ảnh sắc nét và chi tiết hơn.
- Đèn pha và đèn chiếu sáng: Đèn pha sử dụng gương parabol để tập trung ánh sáng, tạo ra luồng sáng mạnh và chiếu xa. Các đèn pin cũng ứng dụng nguyên lý này để tăng cường hiệu quả chiếu sáng.
- Anten parabol: Anten parabol được sử dụng rộng rãi trong viễn thông và truyền thông vệ tinh. Nhờ khả năng tập trung sóng điện từ vào một điểm, anten parabol giúp tăng cường tín hiệu và cải thiện chất lượng truyền phát.
- Kính thiên văn phản xạ: Kính thiên văn phản xạ sử dụng gương parabol để thu và phản chiếu ánh sáng từ các thiên thể, giúp quan sát rõ ràng hơn các vật thể trong không gian.
- Nghiên cứu khoa học: Trong các thí nghiệm về phi trọng lực, quỹ đạo bay hình parabol được sử dụng để tạo ra môi trường không trọng lực trong thời gian ngắn, giúp nghiên cứu và phát triển các ứng dụng khoa học.
Với những ứng dụng đa dạng và phong phú, parabol đã chứng tỏ được vai trò quan trọng trong nhiều lĩnh vực của đời sống.
6. Tài nguyên và công cụ hỗ trợ
Để tính toán diện tích parabol một cách chính xác và hiệu quả, nhiều tài nguyên và công cụ hỗ trợ có sẵn để giúp bạn trong quá trình học tập và làm việc. Dưới đây là một số tài nguyên và công cụ hữu ích:
- Phần mềm tính toán: Các phần mềm như GeoGebra, WolframAlpha cung cấp khả năng tính toán và vẽ đồ thị parabol một cách chính xác.
- Website học tập: Khan Academy, Coursera cung cấp các khóa học và bài giảng về tích phân và hình học giải tích, giúp bạn nắm vững kiến thức về parabol.
- Sách giáo khoa và tài liệu: Các sách giáo khoa chuyên về toán học và tài liệu tham khảo từ các trường đại học cung cấp kiến thức cơ bản và nâng cao về parabol.
- Cộng đồng trực tuyến: Các diễn đàn như Stack Exchange, Reddit có các chuyên gia và người học cùng thảo luận và giải đáp thắc mắc về toán học.
Bằng cách sử dụng các tài nguyên và công cụ hỗ trợ này, bạn có thể nắm vững kiến thức về parabol và áp dụng chúng vào các bài toán thực tế một cách hiệu quả.