Chủ đề diện tích elip: Khám phá chi tiết về diện tích elip với các công thức tính toán, ứng dụng thực tế và các ví dụ minh họa cụ thể. Bài viết này sẽ giúp bạn hiểu rõ hơn về elip và cách tính diện tích của nó, đồng thời giới thiệu những ứng dụng hữu ích trong nhiều lĩnh vực khác nhau.
Mục lục
- Diện tích Elip
- Tổng quan về diện tích elip
- Ví dụ và bài tập minh họa
- Phân tích chi tiết về diện tích elip
- Ứng dụng của diện tích elip trong các lĩnh vực khác nhau
- Các phương pháp đo diện tích elip
- Các bài viết và tài liệu tham khảo
- YOUTUBE: Video giải thích tại sao không có công thức chính xác để tính chu vi hình elip. Khám phá các phương pháp xấp xỉ và lý do toán học đằng sau vấn đề này.
Diện tích Elip
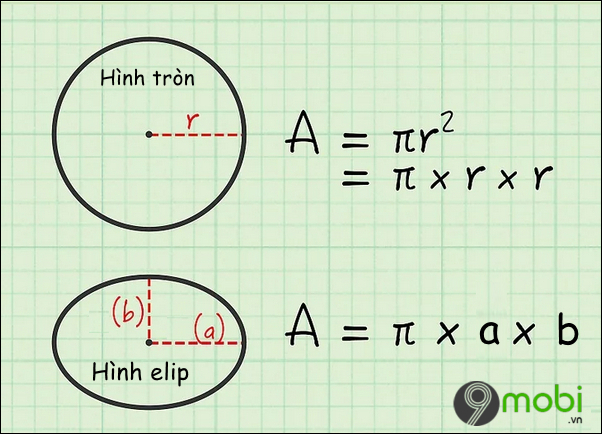
Elip là một hình có hình dạng giống như hình bầu dục, và diện tích của nó có thể được tính bằng công thức toán học. Để tính diện tích của một elip, ta cần biết độ dài của hai bán trục chính.
Công thức tính diện tích elip
Giả sử elip có bán trục chính là a và bán trục phụ là b, công thức tính diện tích S của elip được cho bởi:
\[ S = \pi \times a \times b \]
Giải thích các thành phần trong công thức
- a: Bán trục chính (là khoảng cách từ tâm đến điểm xa nhất trên elip)
- b: Bán trục phụ (là khoảng cách từ tâm đến điểm gần nhất trên elip)
- \(\pi\): Hằng số Pi (khoảng 3.14159)
Ví dụ cụ thể
Giả sử chúng ta có một elip với bán trục chính a = 5 cm và bán trục phụ b = 3 cm. Diện tích của elip này sẽ được tính như sau:
\[ S = \pi \times 5 \times 3 = 15\pi \]
Với \(\pi \approx 3.14159\), ta có:
\[ S \approx 15 \times 3.14159 = 47.12385 \text{ cm}^2 \]
Bảng tính diện tích elip với các giá trị khác nhau
| Bán trục chính (a) | Bán trục phụ (b) | Diện tích (S) |
|---|---|---|
| 2 | 1 | \(2\pi\) |
| 4 | 2 | \(8\pi\) |
| 6 | 3 | \(18\pi\) |
| 8 | 4 | \(32\pi\) |
Tóm tắt
Diện tích của một elip phụ thuộc vào độ dài của bán trục chính và bán trục phụ. Bằng cách sử dụng công thức \[ S = \pi \times a \times b \], chúng ta có thể dễ dàng tính toán diện tích của bất kỳ elip nào nếu biết các thông số cần thiết.

.png)
Tổng quan về diện tích elip
Elip là một hình có dạng bầu dục, giống như một hình tròn bị kéo dãn theo một trục. Đây là một hình học quan trọng trong toán học và có nhiều ứng dụng trong thực tế. Để hiểu rõ hơn về elip, chúng ta sẽ tìm hiểu về các yếu tố cơ bản và công thức tính diện tích của nó.
Các yếu tố cơ bản của elip
- Bán trục chính (a): Khoảng cách từ tâm elip đến điểm xa nhất trên elip.
- Bán trục phụ (b): Khoảng cách từ tâm elip đến điểm gần nhất trên elip.
- Tâm elip: Điểm nằm ở trung tâm của elip, là giao điểm của hai trục đối xứng.
Công thức tính diện tích elip
Diện tích S của elip được tính bằng công thức:
\[ S = \pi \times a \times b \]
Trong đó:
- \(a\): Bán trục chính
- \(b\): Bán trục phụ
- \(\pi\): Hằng số Pi, xấp xỉ 3.14159
Ví dụ cụ thể
Giả sử chúng ta có một elip với bán trục chính a = 6 cm và bán trục phụ b = 4 cm. Diện tích của elip này được tính như sau:
\[ S = \pi \times 6 \times 4 \]
\[ S = 24\pi \]
Với \(\pi \approx 3.14159\), ta có:
\[ S \approx 24 \times 3.14159 = 75.39824 \text{ cm}^2 \]
Bảng giá trị diện tích elip với các bán trục khác nhau
| Bán trục chính (a) | Bán trục phụ (b) | Diện tích (S) |
|---|---|---|
| 2 | 1 | \(2\pi\) |
| 4 | 2 | \(8\pi\) |
| 6 | 3 | \(18\pi\) |
| 8 | 4 | \(32\pi\) |
Kết luận
Diện tích của elip phụ thuộc vào độ dài của hai bán trục chính và bán trục phụ. Với công thức \[ S = \pi \times a \times b \], việc tính toán diện tích elip trở nên đơn giản và dễ dàng hơn. Elip không chỉ là một đối tượng toán học thú vị mà còn có nhiều ứng dụng quan trọng trong khoa học và đời sống.
Ví dụ và bài tập minh họa
Dưới đây là một số ví dụ và bài tập minh họa để giúp bạn hiểu rõ hơn về cách tính diện tích elip.
Ví dụ 1: Tính diện tích elip
Cho một elip có bán trục chính \(a = 6\) cm và bán trục phụ \(b = 4\) cm. Tính diện tích của elip này.
- Xác định các giá trị cần thiết:
- Bán trục chính \(a = 6\) cm
- Bán trục phụ \(b = 4\) cm
- Áp dụng công thức:
\[ S = \pi \times a \times b \]
- Thay các giá trị vào công thức:
\[ S = \pi \times 6 \times 4 \]
\[ S = 24\pi \]
- Tính toán giá trị gần đúng:
\[ S \approx 24 \times 3.14159 = 75.39824 \text{ cm}^2 \]
Ví dụ 2: Tính diện tích elip
Cho một elip có bán trục chính \(a = 8\) cm và bán trục phụ \(b = 5\) cm. Tính diện tích của elip này.
- Xác định các giá trị cần thiết:
- Bán trục chính \(a = 8\) cm
- Bán trục phụ \(b = 5\) cm
- Áp dụng công thức:
\[ S = \pi \times a \times b \]
- Thay các giá trị vào công thức:
\[ S = \pi \times 8 \times 5 \]
\[ S = 40\pi \]
- Tính toán giá trị gần đúng:
\[ S \approx 40 \times 3.14159 = 125.6636 \text{ cm}^2 \]
Bài tập minh họa
Dưới đây là một số bài tập để bạn tự luyện tập.
Bài tập 1
Tính diện tích của elip có bán trục chính \(a = 7\) cm và bán trục phụ \(b = 3\) cm.
Bài tập 2
Tính diện tích của elip có bán trục chính \(a = 10\) cm và bán trục phụ \(b = 6\) cm.
Bài tập 3
Tính diện tích của elip có bán trục chính \(a = 12\) cm và bán trục phụ \(b = 9\) cm.
Bài tập 4
Tính diện tích của elip có bán trục chính \(a = 4\) cm và bán trục phụ \(b = 2\) cm.
Hy vọng những ví dụ và bài tập trên sẽ giúp bạn hiểu rõ hơn về cách tính diện tích elip và áp dụng nó vào các bài toán thực tế.

Phân tích chi tiết về diện tích elip
Elip là một đường cong đóng có hình dạng giống như một hình bầu dục. Để hiểu rõ hơn về diện tích elip, chúng ta sẽ phân tích các yếu tố quan trọng và công thức tính diện tích của nó.
Các yếu tố cấu thành elip
Một elip được xác định bởi hai bán trục chính:
- Bán trục chính (a): Khoảng cách lớn nhất từ tâm đến chu vi của elip.
- Bán trục phụ (b): Khoảng cách ngắn nhất từ tâm đến chu vi của elip.
Công thức tính diện tích elip
Diện tích của một elip được tính bằng công thức:
\[ S = \pi \times a \times b \]
Trong đó:
- \(S\): Diện tích elip
- \(a\): Bán trục chính
- \(b\): Bán trục phụ
- \(\pi\): Hằng số Pi (xấp xỉ 3.14159)
Ví dụ minh họa
Hãy xem xét một elip với bán trục chính \(a = 5\) cm và bán trục phụ \(b = 3\) cm. Diện tích của elip này sẽ được tính như sau:
- Xác định các giá trị:
- Bán trục chính \(a = 5\) cm
- Bán trục phụ \(b = 3\) cm
- Áp dụng công thức:
\[ S = \pi \times a \times b \]
- Thay các giá trị vào công thức:
\[ S = \pi \times 5 \times 3 \]
\[ S = 15\pi \]
- Tính giá trị gần đúng:
\[ S \approx 15 \times 3.14159 = 47.12385 \text{ cm}^2 \]
Bảng phân tích diện tích elip
Dưới đây là bảng phân tích diện tích elip với các giá trị khác nhau của bán trục chính và bán trục phụ:
| Bán trục chính (a) | Bán trục phụ (b) | Diện tích (S) |
|---|---|---|
| 2 | 1 | \(2\pi \approx 6.2832 \text{ cm}^2\) |
| 4 | 2 | \(8\pi \approx 25.1328 \text{ cm}^2\) |
| 6 | 3 | \(18\pi \approx 56.5487 \text{ cm}^2\) |
| 8 | 4 | \(32\pi \approx 100.53096 \text{ cm}^2\) |
Các bước tính diện tích elip chi tiết
- Xác định bán trục chính (a) và bán trục phụ (b) của elip.
- Áp dụng công thức \( S = \pi \times a \times b \).
- Nhân giá trị của \(a\) và \(b\) với hằng số \(\pi\).
- Chuyển đổi kết quả sang đơn vị diện tích thích hợp (ví dụ: cm²).
Việc tính toán diện tích elip đòi hỏi sự hiểu biết về các yếu tố cấu thành elip và áp dụng đúng công thức. Điều này giúp chúng ta áp dụng trong nhiều lĩnh vực khác nhau như kỹ thuật, khoa học và thiết kế.
Ứng dụng của diện tích elip trong các lĩnh vực khác nhau
Diện tích elip có nhiều ứng dụng quan trọng trong các lĩnh vực khác nhau, từ kỹ thuật, khoa học, đến thiết kế và nghệ thuật. Dưới đây là một số ứng dụng nổi bật của diện tích elip.
1. Kỹ thuật và xây dựng
Trong kỹ thuật và xây dựng, elip thường được sử dụng trong thiết kế cầu, mái vòm và các công trình kiến trúc độc đáo. Việc tính toán diện tích elip giúp xác định kích thước và diện tích bề mặt cần thiết cho các cấu trúc này.
2. Thiết kế ô tô và hàng không
Elip được áp dụng trong thiết kế khí động học của ô tô và máy bay. Hình dạng elip giúp giảm lực cản không khí, tăng hiệu suất và tiết kiệm nhiên liệu. Diện tích elip giúp tính toán bề mặt tiếp xúc và lực cản.
3. Y học và sinh học
Trong y học và sinh học, diện tích elip được sử dụng để đo lường và phân tích các cấu trúc sinh học như tế bào, cơ quan và các bộ phận cơ thể. Ví dụ, việc tính diện tích elip của các vùng não giúp trong nghiên cứu và chẩn đoán.
4. Thiết kế và nghệ thuật
Elip là một yếu tố thiết kế phổ biến trong nghệ thuật và đồ họa. Việc tính toán diện tích elip giúp nghệ sĩ và nhà thiết kế tạo ra các hình dạng cân đối và hài hòa. Điều này cũng được áp dụng trong thiết kế nội thất và kiến trúc.
5. Toán học và giáo dục
Trong toán học, diện tích elip là một phần quan trọng trong hình học giải tích. Nó giúp học sinh và sinh viên hiểu về các công thức và tính toán liên quan đến hình học không gian. Diện tích elip cũng được sử dụng trong nhiều bài tập và ví dụ minh họa.
Ví dụ về tính diện tích elip
Hãy xem xét một ví dụ cụ thể để tính diện tích elip với bán trục chính \(a\) và bán trục phụ \(b\).
Công thức tính diện tích elip là:
\[ S = \pi \times a \times b \]
Ví dụ, với \(a = 4\) cm và \(b = 3\) cm, diện tích elip sẽ là:
\[ S = \pi \times 4 \times 3 = 12\pi \]
Thay giá trị \(\pi\) vào, chúng ta có:
\[ S \approx 12 \times 3.14159 = 37.69908 \text{ cm}^2 \]
Bảng ứng dụng của diện tích elip
| Lĩnh vực | Ứng dụng cụ thể |
|---|---|
| Kỹ thuật và xây dựng | Thiết kế cầu, mái vòm, công trình kiến trúc |
| Thiết kế ô tô và hàng không | Thiết kế khí động học |
| Y học và sinh học | Đo lường và phân tích cấu trúc sinh học |
| Thiết kế và nghệ thuật | Tạo hình dạng cân đối, hài hòa |
| Toán học và giáo dục | Giảng dạy và học tập hình học giải tích |
Như vậy, diện tích elip có nhiều ứng dụng quan trọng và đa dạng trong các lĩnh vực khác nhau, góp phần vào sự phát triển và tiến bộ của khoa học và công nghệ.

Các phương pháp đo diện tích elip
Đo diện tích elip là một bài toán thường gặp trong toán học và có thể thực hiện thông qua nhiều phương pháp khác nhau. Dưới đây là một số phương pháp phổ biến để đo diện tích elip:
Sử dụng công thức cơ bản
Phương pháp đơn giản nhất để tính diện tích elip là sử dụng công thức toán học cơ bản:
\[ S = \pi \cdot a \cdot b \]
Trong đó:
- S: Diện tích elip
- \(\pi\): Hằng số toán học Pi (xấp xỉ 3,14)
- a: Bán trục lớn của elip
- b: Bán trục nhỏ của elip
Sử dụng phần mềm tính toán
Có nhiều phần mềm toán học có thể hỗ trợ tính toán diện tích elip, chẳng hạn như MATLAB, GeoGebra hoặc các công cụ trực tuyến khác. Cách thực hiện thường bao gồm:
- Nhập các thông số của elip (bán trục lớn và bán trục nhỏ).
- Sử dụng công cụ tính diện tích để nhận kết quả.
Phương pháp đo trực tiếp
Trong một số trường hợp, đặc biệt là trong ứng dụng thực tế, diện tích elip có thể được đo trực tiếp bằng cách sử dụng các công cụ đo lường vật lý, như:
- Sử dụng giấy vẽ đồ thị và tính số ô vuông bên trong elip.
- Sử dụng các thiết bị đo diện tích kỹ thuật số.
Phương pháp đo gián tiếp
Phương pháp này bao gồm việc sử dụng các thông tin gián tiếp để tính diện tích elip, chẳng hạn như:
- Đo chu vi của elip và sử dụng các công thức liên quan để tính diện tích.
- Sử dụng các phương trình tham số của elip để tính diện tích dựa trên tọa độ các điểm trên đường cong.
Thông qua các phương pháp này, việc đo diện tích elip trở nên dễ dàng và chính xác hơn, đáp ứng nhu cầu của nhiều ứng dụng trong thực tế và nghiên cứu khoa học.
XEM THÊM:
Các bài viết và tài liệu tham khảo
Dưới đây là một số bài viết và tài liệu tham khảo giúp bạn hiểu rõ hơn về diện tích elip, bao gồm các công thức, ví dụ minh họa, và các dạng bài tập liên quan:
-
Chuyên đề Elip luyện thi đại học - Đây là tài liệu đầy đủ lý thuyết và các dạng bài tập từ dễ đến khó, phù hợp cho học sinh chuẩn bị cho kỳ thi đại học.
-
Cách tính diện tích hình Elip - Bài viết này cung cấp công thức tính diện tích elip, hướng dẫn từng bước cách tính, và ví dụ minh họa cụ thể.
-
Hình elip - Lý thuyết và các dạng bài tập - Tài liệu này bao gồm lý thuyết và các dạng bài tập về elip, từ cơ bản đến nâng cao, giúp học sinh làm quen và thực hành.
Ngoài ra, để hiểu rõ hơn về các công thức liên quan đến diện tích elip, bạn có thể tham khảo các tài liệu sau:
-
Công thức tính diện tích hình Elip - Bài viết này trên QuanTriMang cung cấp một cái nhìn tổng quan về công thức tính diện tích của hình elip, cùng với các ví dụ minh họa.
-
Các dạng bài tập về đường elip - Tài liệu này bao gồm nhiều dạng bài tập về đường elip, giúp học sinh nắm vững kiến thức và áp dụng vào thực tế.