Chủ đề dạng toán chuyển động cùng chiều: Khám phá toàn diện về dạng toán chuyển động cùng chiều với hướng dẫn chi tiết và các bài tập thực hành hữu ích. Bài viết này cung cấp cái nhìn sâu sắc về khái niệm cơ bản, phương pháp giải toán, cũng như những ứng dụng thực tiễn để giúp bạn nắm vững và áp dụng hiệu quả trong học tập và thi cử.
Mục lục
Dạng Toán Chuyển Động Cùng Chiều
Dạng toán chuyển động cùng chiều là một chủ đề phổ biến trong môn toán học, đặc biệt là trong các bài toán liên quan đến chuyển động và tốc độ. Dưới đây là một số thông tin chi tiết về dạng toán này:
Khái Niệm Cơ Bản
Dạng toán chuyển động cùng chiều liên quan đến việc giải các bài toán mà trong đó có hai hoặc nhiều đối tượng di chuyển theo cùng một hướng. Mục tiêu của dạng toán này thường là tính toán thời gian, khoảng cách hoặc vận tốc của các đối tượng dựa trên các điều kiện cho trước.
Các Loại Bài Toán Phổ Biến
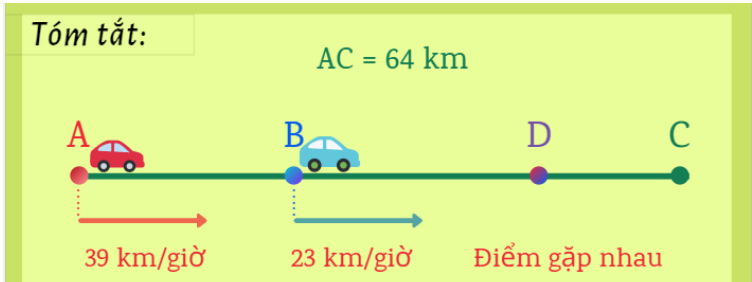
- Bài toán về hai đối tượng di chuyển cùng chiều: Ví dụ như hai xe ô tô đi cùng chiều, một xe nhanh hơn và cần tính thời gian mà xe nhanh hơn sẽ bắt kịp xe chậm hơn.
- Bài toán về chuyển động với tốc độ khác nhau: Trong trường hợp này, bài toán yêu cầu tính toán sự khác biệt về khoảng cách giữa hai đối tượng di chuyển với tốc độ khác nhau.
- Bài toán ứng dụng trong đời sống: Ví dụ như bài toán liên quan đến việc tính toán thời gian giao hàng, hoặc thời gian hai người gặp nhau trong khi di chuyển cùng chiều.
Ví Dụ Cụ Thể
| Ví Dụ | Giải Pháp |
|---|---|
| Hai xe ô tô cùng đi về một hướng, xe A đi nhanh hơn xe B. Tính thời gian để xe A vượt xe B. | Sử dụng công thức: T = (Khoảng cách giữa xe A và xe B) / (Tốc độ của xe A - Tốc độ của xe B) |
| Hai người đi bộ cùng một hướng từ hai điểm khác nhau, tính thời gian để họ gặp nhau nếu biết tốc độ và khoảng cách. | Sử dụng công thức tương tự như trên, với tốc độ của hai người và khoảng cách giữa họ. |
Ứng Dụng Trong Học Tập
Dạng toán chuyển động cùng chiều giúp học sinh phát triển kỹ năng giải quyết vấn đề, áp dụng các công thức toán học vào tình huống thực tế, và cải thiện khả năng phân tích và tư duy logic.

.png)
1. Giới Thiệu Về Dạng Toán Chuyển Động Cùng Chiều
Dạng toán chuyển động cùng chiều là một phần quan trọng trong môn Toán học, thường xuất hiện trong các bài tập và bài kiểm tra. Đây là loại bài toán mô tả các đối tượng di chuyển theo cùng một hướng, với các tốc độ khác nhau hoặc cùng tốc độ, và yêu cầu người giải tìm ra các thông tin liên quan như thời gian, khoảng cách hoặc tốc độ tương đối.
Để hiểu rõ hơn về dạng toán này, chúng ta cần làm quen với những khái niệm cơ bản sau:
- Khái Niệm Cơ Bản: Trong bài toán chuyển động cùng chiều, các đối tượng di chuyển trên cùng một đường thẳng theo cùng một hướng. Ví dụ, hai xe ô tô chạy trên cùng một đường và có thể có tốc độ khác nhau.
- Ý Nghĩa Và Ứng Dụng: Dạng toán này giúp học sinh phát triển kỹ năng phân tích và giải quyết vấn đề. Nó không chỉ xuất hiện trong các bài tập toán mà còn trong các tình huống thực tế như giao thông và vận chuyển hàng hóa.
Các công thức cơ bản trong dạng toán này bao gồm:
- Công Thức Tốc Độ: \( v = \frac{s}{t} \), trong đó \( v \) là tốc độ, \( s \) là khoảng cách, và \( t \) là thời gian.
- Công Thức Khoảng Cách: \( s = v \times t \), giúp tính toán khoảng cách dựa trên tốc độ và thời gian.
- Công Thức Thời Gian: \( t = \frac{s}{v} \), dùng để xác định thời gian khi biết khoảng cách và tốc độ.
Bằng việc áp dụng những công thức này, bạn sẽ có thể giải quyết các bài toán chuyển động cùng chiều một cách chính xác và hiệu quả.
2. Các Loại Bài Toán Phổ Biến
Dạng toán chuyển động cùng chiều bao gồm nhiều loại bài toán khác nhau, mỗi loại có những yêu cầu và đặc điểm riêng. Dưới đây là các loại bài toán phổ biến mà bạn có thể gặp:
- Bài Toán Về Hai Đối Tượng Di Chuyển Cùng Chiều:
Loại bài toán này thường yêu cầu bạn tính toán khoảng cách hoặc thời gian khi hai đối tượng di chuyển cùng chiều với tốc độ khác nhau. Ví dụ, hai xe ô tô chạy trên cùng một đường với tốc độ khác nhau, và bạn cần xác định khi nào chúng sẽ gặp nhau hoặc khoảng cách giữa chúng tại một thời điểm nhất định.
- Bài Toán Về Tốc Độ Khác Nhau:
Trong bài toán này, bạn sẽ phải giải quyết các vấn đề liên quan đến việc so sánh tốc độ của các đối tượng. Ví dụ, nếu một xe chạy nhanh hơn xe còn lại, bài toán có thể yêu cầu bạn tính toán thời gian mà xe nhanh hơn sẽ đuổi kịp xe chậm hơn hoặc khoảng cách giữa hai xe tại một thời điểm cụ thể.
- Bài Toán Ứng Dụng Trong Đời Sống:
Loại bài toán này liên quan đến các tình huống thực tế như giao thông hoặc vận chuyển hàng hóa. Ví dụ, bạn có thể gặp bài toán yêu cầu tính toán thời gian cần thiết để một chuyến hàng đến nơi đích khi hai phương tiện cùng di chuyển theo cùng một hướng nhưng với tốc độ khác nhau.
Những loại bài toán này giúp bạn rèn luyện kỹ năng phân tích và áp dụng các công thức toán học vào các tình huống thực tế, đồng thời nâng cao khả năng giải quyết vấn đề một cách nhanh chóng và chính xác.

3. Phương Pháp Giải Toán
Để giải các bài toán chuyển động cùng chiều một cách hiệu quả, bạn có thể áp dụng các phương pháp cơ bản sau:
- Hiểu Đề Bài:
Trước tiên, hãy đọc kỹ đề bài để xác định các thông tin cần thiết như tốc độ, khoảng cách và thời gian. Xác định rõ các đối tượng chuyển động và các điều kiện liên quan.
- Chọn Công Thức Phù Hợp:
Sử dụng các công thức cơ bản để giải bài toán. Các công thức thường dùng bao gồm:
- Công Thức Tốc Độ: \( v = \frac{s}{t} \)
- Công Thức Khoảng Cách: \( s = v \times t \)
- Công Thức Thời Gian: \( t = \frac{s}{v} \)
- Thiết Lập Phương Trình:
Đặt các yếu tố vào các phương trình dựa trên thông tin đã cho. Ví dụ, nếu hai đối tượng di chuyển với tốc độ khác nhau và bạn cần tính khoảng cách giữa chúng, bạn có thể thiết lập phương trình để giải.
- Giải Phương Trình:
Giải các phương trình đã thiết lập để tìm ra kết quả. Kiểm tra lại các phép toán để đảm bảo tính chính xác.
- Kiểm Tra Kết Quả:
Xem xét lại kết quả để đảm bảo nó hợp lý với tình huống thực tế. Đôi khi, việc so sánh kết quả với dữ liệu gốc có thể giúp xác định lỗi.
Bằng cách áp dụng các phương pháp này, bạn sẽ có thể giải quyết các bài toán chuyển động cùng chiều một cách hiệu quả và chính xác hơn.

4. Ví Dụ Cụ Thể Và Giải Pháp
Dưới đây là một số ví dụ cụ thể về dạng toán chuyển động cùng chiều và cách giải quyết chúng:
4.1 Ví Dụ Về Hai Xe Ô Tô Cùng Chiều
Hai xe ô tô A và B cùng di chuyển trên cùng một đường. Xe A xuất phát trước và có tốc độ 60 km/h, còn xe B có tốc độ 80 km/h. Tính thời gian để xe B đuổi kịp xe A nếu khoảng cách giữa chúng là 90 km.
- Thiết Lập Phương Trình: Để tính thời gian xe B đuổi kịp xe A, ta cần xác định khoảng cách xe B cần vượt qua. Khoảng cách cần vượt qua là 90 km, và tốc độ tương đối giữa hai xe là \( 80 - 60 = 20 \) km/h.
- Tính Thời Gian: Thời gian để xe B đuổi kịp xe A được tính bằng: \[ t = \frac{90}{20} = 4.5 \text{ giờ} \]
- Kết Quả: Xe B sẽ đuổi kịp xe A sau 4.5 giờ.
4.2 Ví Dụ Về Hai Người Đi Bộ
Hai người đi bộ, người thứ nhất xuất phát từ điểm A với tốc độ 5 km/h và người thứ hai xuất phát từ điểm B cách A 30 km với tốc độ 4 km/h. Tính thời gian để hai người gặp nhau nếu họ đi theo cùng một hướng.
- Thiết Lập Phương Trình: Để tính thời gian gặp nhau, ta tính tốc độ tương đối của hai người. Tốc độ tương đối là \( 5 - 4 = 1 \) km/h, và khoảng cách ban đầu giữa họ là 30 km.
- Tính Thời Gian: Thời gian để họ gặp nhau là: \[ t = \frac{30}{1} = 30 \text{ giờ} \]
- Kết Quả: Hai người sẽ gặp nhau sau 30 giờ.
Các ví dụ trên giúp bạn hiểu rõ cách áp dụng các công thức và phương pháp để giải quyết các bài toán chuyển động cùng chiều trong thực tế.

5. Hướng Dẫn Và Bài Tập Thực Hành
Để nắm vững dạng toán chuyển động cùng chiều, việc thực hành với các bài tập cụ thể là rất quan trọng. Dưới đây là hướng dẫn chi tiết và một số bài tập thực hành để giúp bạn cải thiện kỹ năng giải toán của mình:
5.1 Hướng Dẫn Chi Tiết
Để giải quyết các bài toán chuyển động cùng chiều, hãy làm theo các bước sau:
- Đọc Kỹ Đề Bài: Xác định các thông tin cần thiết như tốc độ, khoảng cách, và thời gian. Hiểu rõ tình huống và các yêu cầu của bài toán.
- Chọn Công Thức Phù Hợp: Lựa chọn công thức toán học phù hợp với tình huống, ví dụ: công thức tính tốc độ, khoảng cách, hoặc thời gian.
- Thiết Lập Phương Trình: Đưa các thông tin vào các phương trình đã chọn để thiết lập một bài toán cụ thể.
- Giải Phương Trình: Thực hiện các phép toán cần thiết để giải phương trình và tìm ra kết quả.
- Kiểm Tra Kết Quả: Xem xét lại kết quả để đảm bảo tính chính xác và hợp lý với các dữ liệu ban đầu.
5.2 Bài Tập Đề Xuất Và Giải Đáp
- Bài Tập 1: Hai xe đạp, một xe đi với tốc độ 12 km/h và một xe đi với tốc độ 15 km/h, xuất phát cùng lúc từ cùng một điểm. Tính thời gian để xe đi nhanh hơn vượt qua xe đi chậm hơn nếu khoảng cách giữa hai xe lúc bắt đầu là 20 km.
Giải Đáp: Tốc độ tương đối giữa hai xe là \( 15 - 12 = 3 \) km/h. Thời gian để vượt qua là:
\[
t = \frac{20}{3} \approx 6.67 \text{ giờ}
\] - Bài Tập 2: Một người đi bộ từ điểm A với tốc độ 4 km/h, và một người khác xuất phát từ điểm B cách A 40 km với tốc độ 5 km/h. Tính thời gian để hai người gặp nhau nếu họ đi theo cùng một hướng.
Giải Đáp: Tốc độ tương đối là \( 5 - 4 = 1 \) km/h. Thời gian để gặp nhau là:
\[
t = \frac{40}{1} = 40 \text{ giờ}
\]
Thực hành các bài tập này sẽ giúp bạn làm quen với các loại bài toán chuyển động cùng chiều và cải thiện khả năng giải quyết vấn đề của mình.
XEM THÊM:
6. Lợi Ích Khi Nắm Vững Dạng Toán Này
Nắm vững dạng toán chuyển động cùng chiều mang lại nhiều lợi ích đáng kể, không chỉ trong học tập mà còn trong các tình huống thực tế. Dưới đây là một số lợi ích nổi bật:
- Phát Triển Kỹ Năng Giải Quyết Vấn Đề:
Khi bạn hiểu rõ các phương pháp và công thức liên quan đến chuyển động cùng chiều, bạn sẽ phát triển khả năng phân tích và giải quyết các vấn đề phức tạp. Điều này giúp cải thiện kỹ năng tư duy logic và tính toán của bạn.
- Cải Thiện Hiệu Quả Trong Học Tập:
Dạng toán này thường xuất hiện trong các kỳ thi và bài kiểm tra. Việc nắm vững nó sẽ giúp bạn làm bài nhanh chóng và chính xác hơn, từ đó nâng cao điểm số và thành tích học tập.
- Ứng Dụng Trong Đời Sống:
Hiểu biết về chuyển động cùng chiều giúp bạn áp dụng các nguyên tắc toán học vào các tình huống thực tế, như tính toán thời gian đi lại, kế hoạch vận chuyển, và nhiều lĩnh vực khác trong cuộc sống hàng ngày.
- Tăng Cường Kỹ Năng Phân Tích:
Việc làm quen với dạng toán này giúp bạn phát triển khả năng phân tích và lập kế hoạch, điều này có thể hữu ích trong nhiều tình huống khác ngoài toán học, chẳng hạn như trong công việc và các dự án cá nhân.
Với những lợi ích này, việc nắm vững dạng toán chuyển động cùng chiều không chỉ giúp bạn trong học tập mà còn hỗ trợ bạn trong việc áp dụng toán học vào các tình huống thực tế và phát triển kỹ năng cá nhân.