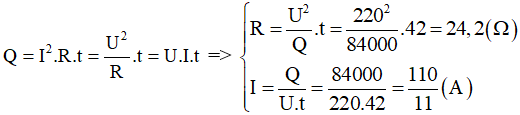Công Thức Tính Nhiệt Lượng Tỏa Ra Trên Điện Trở: Hướng Dẫn Chi Tiết & Ứng Dụng Thực Tế

Khi dòng điện chạy qua điện trở, nhiệt lượng tỏa ra có thể được tính bằng công thức:

\(Q = I^2 \cdot R \cdot t\)

Trong đó:

• Q: Nhiệt lượng tỏa ra (đơn vị: Joules, J)
• I: Cường độ dòng điện chạy qua điện trở (đơn vị: Ampe, A)
• R: Điện trở của dây dẫn (đơn vị: Ohm, Ω)
• t: Thời gian dòng điện chạy qua (đơn vị: giây, s)

Ứng Dụng Thực Tế

Công thức trên được áp dụng rộng rãi trong các tính toán liên quan đến mạch điện. Dưới đây là một số ví dụ minh họa:

Ví Dụ 1: Tính Nhiệt Lượng Tỏa Ra Trên Điện Trở

Giả sử bạn có một điện trở \(R = 10Ω\) và dòng điện qua nó có cường độ \(I = 2A\). Nếu dòng điện chạy trong 5 giây, nhiệt lượng tỏa ra sẽ được tính như sau:

\(Q = 2^2 \cdot 10 \cdot 5 = 200J\)

Ví Dụ 2: Mạch Điện Nối Tiếp

Cho mạch có hai điện trở \(R_1 = 10Ω\) và \(R_2 = 20Ω\) mắc nối tiếp, được cấp một hiệu điện thế \(U = 30V\). Cường độ dòng điện trong mạch là \(I = 1A\). Nhiệt lượng tỏa ra trên mỗi điện trở sau 5 giây là:

• Nhiệt lượng tỏa ra trên \(R_1\): \(Q_1 = 1^2 \cdot 10 \cdot 5 = 50J\)
• Nhiệt lượng tỏa ra trên \(R_2\): \(Q_2 = 1^2 \cdot 20 \cdot 5 = 100J\)

Ví Dụ 3: Mạch Điện Song Song

Trong một mạch song song với hai điện trở \(R_1 = 10Ω\) và \(R_2 = 20Ω\), mỗi điện trở chịu một hiệu điện thế \(U = 30V\). Cường độ dòng điện qua từng điện trở là:

• Cường độ dòng điện qua \(R_1\): \(I_1 = \frac{30V}{10Ω} = 3A\)
• Cường độ dòng điện qua \(R_2\): \(I_2 = \frac{30V}{20Ω} = 1.5A\)

Nhiệt lượng tỏa ra sau 5 giây trên mỗi điện trở:

• \(Q_1 = 3^2 \cdot 10 \cdot 5 = 450J\)
• \(Q_2 = 1.5^2 \cdot 20 \cdot 5 = 225J\)

Chuyển Đổi Đơn Vị

Lưu ý rằng nhiệt lượng thường được chuyển đổi giữa các đơn vị phổ biến như Joule (J), Calo (cal), và Kilocalo (kcal):

• 1J = 0.24 cal
• 1 cal = 4.18 J
• 1 kcal = 1000 cal

Nhiệt lượng tỏa ra trên điện trở là một khái niệm quan trọng trong lĩnh vực điện học, được xác định bằng công thức sau:

\(Q = I^2 \cdot R \cdot t\)

Trong đó:

• Q: Nhiệt lượng tỏa ra (đơn vị: Joules, J)
• I: Cường độ dòng điện chạy qua điện trở (đơn vị: Ampe, A)
• R: Điện trở của dây dẫn (đơn vị: Ohm, Ω)
• t: Thời gian dòng điện chạy qua (đơn vị: giây, s)

Để tính toán nhiệt lượng tỏa ra, ta có thể thực hiện các bước sau:

1. Xác định giá trị cường độ dòng điện \(I\) chạy qua điện trở.
2. Xác định giá trị điện trở \(R\) của dây dẫn hoặc đoạn mạch.
3. Xác định thời gian \(t\) mà dòng điện đã chạy qua điện trở.
4. Sử dụng công thức \(Q = I^2 \cdot R \cdot t\) để tính toán nhiệt lượng tỏa ra.

Ví dụ: Nếu bạn có một điện trở \(R = 10Ω\), dòng điện \(I = 2A\), và dòng điện chạy qua điện trở này trong 5 giây, nhiệt lượng tỏa ra sẽ là:

\(Q = 2^2 \cdot 10 \cdot 5 = 200J\)

Đây là công thức cơ bản, nhưng nó có thể được mở rộng để áp dụng trong các trường hợp phức tạp hơn như mạch nối tiếp, mạch song song hoặc các bài toán thực tế khác.

Dưới đây là một số bài tập minh họa để giúp bạn hiểu rõ hơn về cách áp dụng công thức tính nhiệt lượng tỏa ra trên điện trở:

Bài Tập 1: Điện Trở Đơn

Giả sử có một điện trở \(R = 15Ω\) được mắc vào một nguồn điện, dòng điện qua điện trở là \(I = 3A\). Tính nhiệt lượng tỏa ra trên điện trở trong 10 giây.

1. Xác định các giá trị: \(R = 15Ω\), \(I = 3A\), \(t = 10s\).
2. Áp dụng công thức:

   \(Q = I^2 \cdot R \cdot t\)

3. Thay các giá trị vào công thức:

   \(Q = 3^2 \cdot 15 \cdot 10 = 1350J\)

4. Kết quả: Nhiệt lượng tỏa ra là 1350 Joules.

Bài Tập 2: Mạch Điện Nối Tiếp

Một mạch điện gồm hai điện trở \(R_1 = 10Ω\) và \(R_2 = 20Ω\) được mắc nối tiếp và nối với nguồn điện có hiệu điện thế \(U = 60V\). Tính nhiệt lượng tỏa ra trên mỗi điện trở sau 5 giây.

1. Tổng điện trở của mạch:

   \(R_t = R_1 + R_2 = 10Ω + 20Ω = 30Ω\)

2. Cường độ dòng điện trong mạch:

   \(I = \frac{U}{R_t} = \frac{60V}{30Ω} = 2A\)

3. Nhiệt lượng tỏa ra trên \(R_1\):

   \(Q_1 = I^2 \cdot R_1 \cdot t = 2^2 \cdot 10 \cdot 5 = 200J\)

4. Nhiệt lượng tỏa ra trên \(R_2\):

   \(Q_2 = I^2 \cdot R_2 \cdot t = 2^2 \cdot 20 \cdot 5 = 400J\)

5. Kết quả: Nhiệt lượng tỏa ra trên \(R_1\) là 200 Joules và trên \(R_2\) là 400 Joules.

Bài Tập 3: Mạch Điện Song Song

Một mạch điện có hai điện trở \(R_1 = 5Ω\) và \(R_2 = 10Ω\) mắc song song, được nối với nguồn điện có hiệu điện thế \(U = 20V\). Tính nhiệt lượng tỏa ra trên mỗi điện trở sau 8 giây.

1. Cường độ dòng điện qua từng điện trở:
   • Qua \(R_1\):

     \(I_1 = \frac{U}{R_1} = \frac{20V}{5Ω} = 4A\)

   • Qua \(R_2\):

     \(I_2 = \frac{U}{R_2} = \frac{20V}{10Ω} = 2A\)

2. Nhiệt lượng tỏa ra trên \(R_1\):

   \(Q_1 = I_1^2 \cdot R_1 \cdot t = 4^2 \cdot 5 \cdot 8 = 640J\)

3. Nhiệt lượng tỏa ra trên \(R_2\):

   \(Q_2 = I_2^2 \cdot R_2 \cdot t = 2^2 \cdot 10 \cdot 8 = 320J\)

4. Kết quả: Nhiệt lượng tỏa ra trên \(R_1\) là 640 Joules và trên \(R_2\) là 320 Joules.

Trong một số tình huống cụ thể, việc tính toán nhiệt lượng tỏa ra trên điện trở cần phải áp dụng những biến đổi hoặc xem xét những yếu tố đặc biệt. Dưới đây là một số trường hợp đáng chú ý:

1. Điện Trở Biến Thiên Theo Thời Gian

Khi điện trở \(R\) thay đổi theo thời gian, công thức tính nhiệt lượng trở nên phức tạp hơn. Trong trường hợp này, ta cần tích phân công thức cơ bản để tính tổng nhiệt lượng tỏa ra:

\(Q = \int_{0}^{t} I^2(t) \cdot R(t) \, dt\)

Việc này yêu cầu xác định hàm số \(I(t)\) và \(R(t)\) trong khoảng thời gian \(t\), sau đó thực hiện tích phân để tìm \(Q\).

2. Nhiệt Lượng Tỏa Ra Trong Môi Trường Có Thay Đổi Nhiệt Độ

Khi nhiệt độ môi trường xung quanh thay đổi, giá trị của điện trở \(R\) cũng có thể bị ảnh hưởng, đặc biệt đối với các vật liệu có hệ số nhiệt điện trở cao. Trong trường hợp này, công thức có thể cần điều chỉnh để bao gồm sự thay đổi nhiệt độ:

\(R(T) = R_0 \cdot (1 + \alpha \cdot (T - T_0))\)

Trong đó:

• \(R_0\): Điện trở tại nhiệt độ tham chiếu \(T_0\)
• \(\alpha\): Hệ số nhiệt điện trở của vật liệu
• \(T\): Nhiệt độ hiện tại

Sau đó, sử dụng \(R(T)\) trong công thức tính nhiệt lượng để có kết quả chính xác hơn.

3. Tác Động Của Dòng Điện Xung (Pulse Current)

Trong một số ứng dụng, dòng điện không ổn định mà thay đổi theo xung. Khi đó, nhiệt lượng tỏa ra được tính bằng cách tổng hợp nhiệt lượng từ từng xung điện:

• Giả sử có \(n\) xung điện, với mỗi xung có thời gian tồn tại là \(\Delta t_i\) và cường độ dòng điện là \(I_i\).
• Nhiệt lượng tỏa ra từ mỗi xung là \(Q_i = I_i^2 \cdot R \cdot \Delta t_i\).
• Tổng nhiệt lượng tỏa ra là:

  \(Q_{total} = \sum_{i=1}^{n} Q_i = \sum_{i=1}^{n} I_i^2 \cdot R \cdot \Delta t_i\)

4. Mạch Điện Có Nhiều Nguồn Điện

Trong mạch có nhiều nguồn điện với các mức hiệu điện thế khác nhau, cần tính toán nhiệt lượng tỏa ra trên mỗi phần tử riêng lẻ. Trong trường hợp này, áp dụng định luật Ohm và Kirchhoff để tìm dòng điện qua từng điện trở, sau đó tính nhiệt lượng cho mỗi điện trở riêng lẻ:

1. Xác định cường độ dòng điện qua từng điện trở bằng cách áp dụng định luật Kirchhoff.
2. Sử dụng công thức \(Q_i = I_i^2 \cdot R_i \cdot t\) để tính nhiệt lượng tỏa ra trên từng điện trở.
3. Tổng hợp nhiệt lượng tỏa ra từ tất cả các điện trở để có được nhiệt lượng tổng thể.