Công thức tính cảm ứng từ tại tâm vòng dây: Hướng dẫn chi tiết và ứng dụng thực tiễn

Cảm ứng từ tại tâm vòng dây là một khái niệm quan trọng trong lĩnh vực từ trường và điện từ học. Đây là lượng từ trường sinh ra bởi một vòng dây dẫn khi có dòng điện chạy qua.

Định nghĩa cảm ứng từ

Cảm ứng từ, hay còn gọi là từ trường, là một đại lượng vật lý biểu diễn khả năng tác động lực từ lên các hạt điện tích chuyển động hoặc lên các vật có tính chất từ. Đơn vị đo cảm ứng từ là Tesla (T).

Công thức tính cảm ứng từ tại tâm vòng dây

Công thức tính cảm ứng từ tại tâm của một vòng dây dẫn tròn có bán kính \( R \) khi có dòng điện \( I \) chạy qua được xác định bởi biểu thức:

\[
B = \dfrac{\mu_0 \cdot I}{2 \cdot R}
\]

Trong đó:

• \( B \) là cảm ứng từ tại tâm vòng dây (Tesla).
• \( \mu_0 \) là hằng số từ trường trong chân không, với giá trị xấp xỉ \( 4\pi \times 10^{-7} \, \text{T}\cdot\text{m}/\text{A} \).
• \( I \) là cường độ dòng điện chạy qua vòng dây (Ampere).
• \( R \) là bán kính của vòng dây (mét).

Ứng dụng của công thức

Công thức này được ứng dụng rộng rãi trong việc thiết kế các thiết bị điện tử như nam châm điện, cuộn cảm, và các thiết bị đo từ trường. Nó giúp tính toán và dự đoán được cường độ từ trường tại các điểm trong không gian khi biết các yếu tố liên quan như dòng điện và kích thước của vòng dây.

Lưu ý khi sử dụng công thức

• Công thức này chỉ áp dụng cho vòng dây có dạng hình tròn và dòng điện phân bố đều trên vòng dây.
• Trong trường hợp vòng dây có nhiều vòng, cần nhân thêm số vòng dây \( N \) vào công thức, cụ thể là: \[ B = \dfrac{\mu_0 \cdot N \cdot I}{2 \cdot R} \]
• Để tính toán chính xác trong môi trường không phải là chân không, cần sử dụng hằng số từ thẩm \( \mu \) của môi trường đó thay cho \( \mu_0 \).

Cảm ứng từ, hay còn gọi là từ trường, là một đại lượng vật lý quan trọng trong lĩnh vực điện từ học. Nó biểu thị khả năng tác động lực từ lên các hạt điện tích hoặc các vật có từ tính trong không gian xung quanh dòng điện.

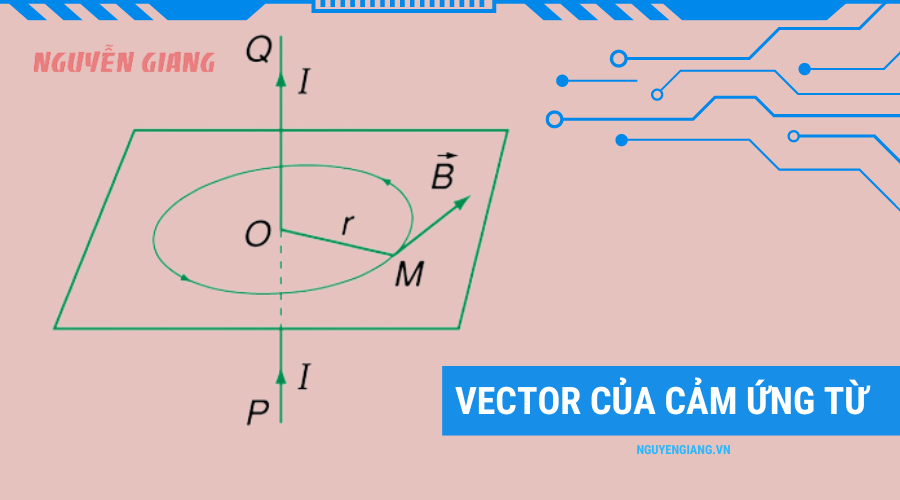
Khi một dòng điện chạy qua một dây dẫn, nó tạo ra một từ trường xung quanh dây dẫn đó. Từ trường này có hướng và cường độ phụ thuộc vào dòng điện và cấu trúc của dây dẫn. Đặc biệt, đối với một vòng dây dẫn tròn, cảm ứng từ tại tâm của vòng dây là một điểm đáng chú ý vì đây là nơi mà từ trường đạt giá trị cực đại trong không gian bên trong vòng dây.

Cảm ứng từ được ký hiệu là \( B \) và đơn vị đo lường là Tesla (T). Công thức tính cảm ứng từ tại tâm vòng dây phụ thuộc vào cường độ dòng điện \( I \) chạy qua dây và bán kính \( R \) của vòng dây.

Tóm lại, việc hiểu và áp dụng công thức tính cảm ứng từ không chỉ giúp chúng ta nắm vững các nguyên lý cơ bản của từ trường mà còn ứng dụng trong nhiều lĩnh vực công nghệ, chẳng hạn như thiết kế nam châm điện, cuộn cảm, và các thiết bị đo từ trường.

Vòng dây là một thành phần quan trọng trong các thiết bị điện từ, được sử dụng rộng rãi trong nhiều ứng dụng như cuộn cảm, máy biến áp, và nam châm điện. Để hiểu rõ hơn về cảm ứng từ tại tâm vòng dây, ta cần nắm vững cấu trúc và nguyên lý hoạt động của nó.

Cấu trúc của vòng dây

• Vòng dây dẫn thường có dạng hình tròn, được làm từ các loại dây dẫn như đồng hoặc nhôm có tính dẫn điện tốt.
• Kích thước của vòng dây được xác định bởi bán kính \( R \), là khoảng cách từ tâm của vòng dây đến bất kỳ điểm nào trên vòng tròn.
• Vòng dây có thể bao gồm một hoặc nhiều vòng, tùy thuộc vào mục đích sử dụng. Số vòng dây được ký hiệu là \( N \).

Nguyên lý hoạt động của vòng dây

1. Tạo ra từ trường: Khi dòng điện \( I \) chạy qua vòng dây, nó sẽ tạo ra một từ trường xung quanh dây dẫn. Từ trường này là kết quả của lực từ sinh ra do chuyển động của các hạt điện tích trong dây dẫn.
2. Tính chất của từ trường: Từ trường này có hướng vuông góc với mặt phẳng chứa vòng dây và cường độ của nó phụ thuộc vào cường độ dòng điện \( I \) cũng như bán kính \( R \) của vòng dây. Công thức tính cảm ứng từ tại tâm vòng dây được cho bởi:

\[
B = \dfrac{\mu_0 \cdot N \cdot I}{2 \cdot R}
\]

1. Cảm ứng từ tại tâm: Tại tâm của vòng dây, các đường sức từ đều hội tụ lại, tạo ra một từ trường mạnh nhất. Đây là lý do tại sao công thức tính cảm ứng từ tại tâm có tầm quan trọng đặc biệt trong các ứng dụng thực tế.
2. Ứng dụng của từ trường trong vòng dây: Từ trường do vòng dây tạo ra được ứng dụng rộng rãi trong thiết kế nam châm điện, cuộn cảm, và các thiết bị đo từ trường, nhờ vào khả năng điều khiển cường độ từ trường bằng cách thay đổi dòng điện hoặc số vòng dây.

Cảm ứng từ tại tâm vòng dây là một trong những khái niệm quan trọng trong lĩnh vực điện từ học. Công thức tính cảm ứng từ này giúp xác định cường độ từ trường tại điểm trung tâm của một vòng dây khi có dòng điện chạy qua. Dưới đây là hướng dẫn chi tiết về công thức này.

Công thức cơ bản

Để tính cảm ứng từ \( B \) tại tâm vòng dây dẫn tròn có bán kính \( R \) và dòng điện \( I \) chạy qua, ta sử dụng công thức:

\[
B = \dfrac{\mu_0 \cdot N \cdot I}{2 \cdot R}
\]

Trong đó:

• \( B \) là cảm ứng từ tại tâm vòng dây (Tesla).
• \( \mu_0 \) là hằng số từ trường trong chân không, với giá trị xấp xỉ \( 4\pi \times 10^{-7} \, \text{T}\cdot\text{m}/\text{A} \).
• \( N \) là số vòng dây.
• \( I \) là cường độ dòng điện chạy qua vòng dây (Ampere).
• \( R \) là bán kính của vòng dây (mét).

Phân tích công thức

• Hằng số từ trường \( \mu_0 \): Hằng số này thể hiện khả năng từ hóa của chân không và là một đại lượng cố định trong tính toán từ trường.
• Số vòng dây \( N \): Cảm ứng từ tỉ lệ thuận với số vòng dây, tức là nếu số vòng dây tăng lên thì cảm ứng từ tại tâm cũng tăng theo.
• Cường độ dòng điện \( I \): Tương tự, cảm ứng từ tỉ lệ thuận với cường độ dòng điện chạy qua vòng dây. Dòng điện càng lớn, từ trường tại tâm càng mạnh.
• Bán kính vòng dây \( R \): Cảm ứng từ tỉ lệ nghịch với bán kính vòng dây. Vòng dây càng nhỏ, từ trường tại tâm càng lớn.

Ví dụ minh họa

Giả sử ta có một vòng dây dẫn với số vòng \( N = 10 \), bán kính \( R = 0,05 \, m \), và dòng điện chạy qua \( I = 2 \, A \). Áp dụng công thức trên, ta tính được cảm ứng từ tại tâm vòng dây như sau:

\[
B = \dfrac{4\pi \times 10^{-7} \cdot 10 \cdot 2}{2 \cdot 0,05} = 2,51 \times 10^{-5} \, T
\]

Kết quả này cho thấy từ trường tại tâm của vòng dây có giá trị \( 2,51 \times 10^{-5} \, T \), là một giá trị nhỏ nhưng rất quan trọng trong các ứng dụng điện từ.

Công thức tính cảm ứng từ tại tâm vòng dây không chỉ mang ý nghĩa lý thuyết mà còn được áp dụng rộng rãi trong nhiều lĩnh vực thực tế, từ thiết kế các thiết bị điện tử đến nghiên cứu khoa học. Dưới đây là một số ứng dụng tiêu biểu của công thức này.

1. Thiết kế nam châm điện

Nam châm điện được sử dụng phổ biến trong nhiều thiết bị, từ động cơ điện đến cần cẩu từ. Công thức tính cảm ứng từ tại tâm vòng dây giúp các kỹ sư thiết kế nam châm điện với cường độ từ trường chính xác, đáp ứng các yêu cầu cụ thể về lực hút và lực đẩy. Bằng cách điều chỉnh số vòng dây \( N \) và cường độ dòng điện \( I \), người ta có thể kiểm soát được độ mạnh yếu của từ trường sinh ra.

2. Chế tạo cuộn cảm

Cuộn cảm là một thành phần không thể thiếu trong các mạch điện tử, đặc biệt là trong các bộ lọc và mạch cộng hưởng. Công thức cảm ứng từ tại tâm vòng dây được sử dụng để tính toán từ trường bên trong cuộn cảm, từ đó xác định các thông số quan trọng như độ tự cảm \( L \). Điều này giúp tối ưu hóa thiết kế cuộn cảm để đạt hiệu suất cao nhất trong mạch điện.

3. Đo lường từ trường

Các thiết bị đo từ trường, chẳng hạn như từ kế, cũng ứng dụng công thức này để hiệu chuẩn và đo lường chính xác cường độ từ trường trong môi trường khác nhau. Điều này rất quan trọng trong các nghiên cứu khoa học, nơi cần độ chính xác cao trong việc đo từ trường của các vật thể hoặc môi trường nghiên cứu.

4. Nghiên cứu khoa học và giáo dục

Công thức tính cảm ứng từ tại tâm vòng dây là một phần quan trọng trong giáo trình vật lý ở các cấp học. Nó không chỉ giúp học sinh, sinh viên hiểu rõ hơn về nguyên lý từ trường mà còn cung cấp công cụ để thực hiện các thí nghiệm đo lường và kiểm chứng lý thuyết từ học. Trong nghiên cứu khoa học, công thức này hỗ trợ việc tính toán và mô phỏng các hiện tượng liên quan đến từ trường.

Tóm lại, công thức tính cảm ứng từ tại tâm vòng dây đóng vai trò quan trọng trong nhiều ứng dụng thực tế, từ thiết kế kỹ thuật đến nghiên cứu khoa học, giúp nâng cao hiệu quả và độ chính xác trong nhiều lĩnh vực.

Khi tính toán cảm ứng từ tại tâm vòng dây, có nhiều yếu tố có thể ảnh hưởng đến độ chính xác của kết quả. Việc hiểu rõ và kiểm soát các yếu tố này là rất quan trọng để đảm bảo rằng các tính toán và ứng dụng trong thực tế đạt được hiệu quả cao nhất.

1. Độ chính xác của các thông số đầu vào

• Bán kính vòng dây \( R \): Độ chính xác của bán kính \( R \) là yếu tố then chốt trong việc tính toán cảm ứng từ. Một sai lệch nhỏ trong việc đo bán kính có thể dẫn đến sai số lớn trong kết quả cuối cùng.
• Cường độ dòng điện \( I \): Dòng điện \( I \) cần được đo và duy trì ổn định trong suốt quá trình tính toán. Các biến đổi nhỏ trong dòng điện có thể ảnh hưởng trực tiếp đến cường độ từ trường tại tâm vòng dây.
• Số vòng dây \( N \): Việc đếm chính xác số vòng dây là điều cần thiết. Bất kỳ sự nhầm lẫn nào trong việc xác định số vòng dây sẽ dẫn đến sai lệch trong kết quả tính toán.

2. Ảnh hưởng của môi trường xung quanh

• Từ trường ngoài: Các từ trường bên ngoài, chẳng hạn như từ trường Trái Đất hoặc từ trường từ các thiết bị điện tử lân cận, có thể làm sai lệch kết quả đo từ trường tại tâm vòng dây. Do đó, cần thực hiện các biện pháp che chắn từ trường nếu có thể.
• Nhiệt độ: Nhiệt độ ảnh hưởng đến tính chất dẫn điện của dây dẫn, từ đó ảnh hưởng đến cường độ dòng điện và cảm ứng từ sinh ra. Cần đảm bảo rằng vòng dây hoạt động trong một môi trường nhiệt độ ổn định để duy trì độ chính xác.
• Chất liệu của lõi: Nếu vòng dây có lõi, chất liệu của lõi sẽ ảnh hưởng lớn đến cảm ứng từ. Lõi làm từ vật liệu có độ từ thẩm cao sẽ tăng cường từ trường, trong khi lõi làm từ vật liệu không từ tính sẽ không ảnh hưởng hoặc có thể làm giảm từ trường.

3. Sai số trong thiết bị đo

• Sai số của dụng cụ đo: Các dụng cụ đo cường độ dòng điện, bán kính và từ trường cần được hiệu chuẩn chính xác. Sai số trong các dụng cụ đo này sẽ dẫn đến sai số trong kết quả tính toán.
• Thời điểm đo: Thời điểm đo cũng quan trọng, đặc biệt là trong các hệ thống có dòng điện thay đổi theo thời gian. Cần đảm bảo đo tại thời điểm dòng điện ổn định để có kết quả chính xác.

4. Cách khắc phục và giảm thiểu sai số

• Sử dụng thiết bị đo chính xác cao: Đảm bảo sử dụng các thiết bị đo có độ chính xác cao và đã được hiệu chuẩn thường xuyên.
• Thực hiện các biện pháp che chắn từ trường: Giảm thiểu ảnh hưởng của các từ trường ngoài bằng cách sử dụng các vật liệu che chắn từ trường thích hợp.
• Kiểm soát môi trường: Đảm bảo môi trường đo lường ổn định về nhiệt độ và không có các yếu tố gây nhiễu từ trường.
• Thực hiện nhiều lần đo: Để tăng độ tin cậy, thực hiện nhiều lần đo và lấy giá trị trung bình sẽ giúp giảm thiểu sai số ngẫu nhiên.

Tóm lại, việc nắm vững các yếu tố ảnh hưởng đến độ chính xác khi tính toán cảm ứng từ tại tâm vòng dây sẽ giúp đảm bảo kết quả đúng đắn và đáng tin cậy, đồng thời nâng cao hiệu quả trong các ứng dụng thực tế.

Trong bài viết này, chúng ta đã tìm hiểu về cảm ứng từ tại tâm vòng dây, từ khái niệm cơ bản đến các ứng dụng thực tế. Công thức tính cảm ứng từ tại tâm vòng dây là một công cụ quan trọng trong việc phân tích và thiết kế các thiết bị liên quan đến từ trường.

Công thức cơ bản để tính cảm ứng từ tại tâm vòng dây là:

\[
B = \frac{{\mu_0 \cdot I}}{{2 \cdot R}}
\]

Trong đó:

• \(B\) là cảm ứng từ tại tâm vòng dây (Tesla)
• \(\mu_0\) là hằng số từ môi trường (T·m/A)
• \(I\) là dòng điện chạy qua vòng dây (Ampe)
• \(R\) là bán kính của vòng dây (mét)

Việc hiểu và áp dụng đúng công thức này là rất quan trọng trong nhiều lĩnh vực của vật lý và kỹ thuật, như thiết kế nam châm điện, chế tạo cuộn cảm, và các thiết bị đo từ trường.

Bằng cách nắm vững công thức và ý nghĩa của các đại lượng trong đó, chúng ta có thể dự đoán và kiểm soát tốt hơn các yếu tố ảnh hưởng đến từ trường trong thực tế. Đặc biệt, việc hiểu rõ các yếu tố như hình dạng, kích thước của vòng dây và môi trường xung quanh sẽ giúp tối ưu hóa độ chính xác trong các ứng dụng cụ thể.

Tóm lại, công thức tính cảm ứng từ tại tâm vòng dây không chỉ là một lý thuyết hàn lâm mà còn có nhiều ứng dụng thực tiễn quan trọng. Việc hiểu và áp dụng đúng công thức này không chỉ giúp cải thiện hiệu suất của các thiết bị liên quan đến từ trường mà còn đóng góp vào sự phát triển của khoa học và công nghệ.