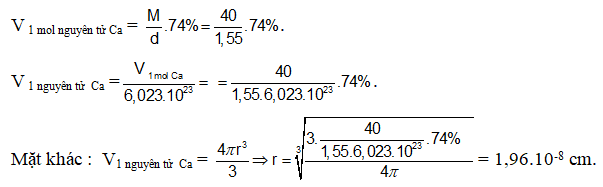Cách Tính Khối Lượng Tuyệt Đối Của Một Nguyên Tử: Hướng Dẫn Chi Tiết Từ Cơ Bản Đến Nâng Cao

Khối lượng tuyệt đối của một nguyên tử là một khái niệm quan trọng trong hóa học và vật lý, được đo lường bằng đơn vị kilogram (kg) hoặc gram (g). Khối lượng này là tổng của khối lượng proton, neutron và electron trong nguyên tử, tuy nhiên, do khối lượng của electron rất nhỏ nên thường được bỏ qua trong các tính toán đơn giản.

1. Công Thức Tính Khối Lượng Tuyệt Đối

Khối lượng tuyệt đối của một nguyên tử có thể được tính toán dựa trên công thức sau:

\[
\text{Khối lượng tuyệt đối} = \frac{\text{Số proton} \times \text{Khối lượng proton} + \text{Số neutron} \times \text{Khối lượng neutron}}{\text{Số Avogadro}}
\]

Trong đó:

• Số proton: Số lượng proton trong hạt nhân của nguyên tử.
• Số neutron: Số lượng neutron trong hạt nhân của nguyên tử.
• Khối lượng proton: Khoảng \(1.6726 \times 10^{-27}\) kg.
• Khối lượng neutron: Khoảng \(1.6750 \times 10^{-27}\) kg.
• Số Avogadro: \(6.022 \times 10^{23}\), số lượng nguyên tử trong một mol chất.

2. Ví Dụ Tính Toán

Giả sử chúng ta muốn tính khối lượng tuyệt đối của một nguyên tử cacbon (\(^{12}C\)), ta có các thông số:

• Số proton: 6
• Số neutron: 6
• Khối lượng proton: \(1.6726 \times 10^{-27}\) kg
• Khối lượng neutron: \(1.6750 \times 10^{-27}\) kg

Áp dụng công thức:

\[
\text{Khối lượng tuyệt đối của } ^{12}C = \frac{(6 \times 1.6726 \times 10^{-27}) + (6 \times 1.6750 \times 10^{-27})}{6.022 \times 10^{23}}
\]

Kết quả tính toán sẽ cho ra khối lượng tuyệt đối của nguyên tử \(^{12}C\) bằng khoảng \(1.9926 \times 10^{-26}\) kg.

3. Ý Nghĩa Của Khối Lượng Tuyệt Đối

Khối lượng tuyệt đối của một nguyên tử giúp chúng ta hiểu rõ hơn về cấu trúc và tính chất của các nguyên tử và phân tử. Đây là cơ sở để so sánh khối lượng của các nguyên tử khác nhau và để tính toán các phản ứng hóa học trong phòng thí nghiệm và thực tiễn.

Khối lượng tuyệt đối của một nguyên tử là một khái niệm quan trọng trong hóa học và vật lý, giúp xác định khối lượng thực tế của một nguyên tử đơn lẻ. Khối lượng này bao gồm tổng khối lượng của các proton, neutron và electron trong nguyên tử.

Trong đó, khối lượng của các hạt proton và neutron là chủ yếu, vì khối lượng của electron rất nhỏ so với hai loại hạt còn lại. Khối lượng tuyệt đối thường được tính bằng đơn vị kilogram (kg) và được xác định dựa trên các phương pháp đo lường chính xác.

Một nguyên tử bao gồm:

• Proton: Có khối lượng khoảng \[1.6726 \times 10^{-27}\] kg.
• Neutron: Có khối lượng khoảng \[1.6750 \times 10^{-27}\] kg.
• Electron: Có khối lượng rất nhỏ, khoảng \[9.109 \times 10^{-31}\] kg, thường được bỏ qua trong tính toán khối lượng tuyệt đối.

Khối lượng tuyệt đối được tính toán bằng cách cộng tổng khối lượng của các proton và neutron, sau đó chia cho số Avogadro \(\approx 6.022 \times 10^{23}\), đây là số lượng nguyên tử trong một mol chất.

Hiểu được khối lượng tuyệt đối của nguyên tử giúp các nhà khoa học và kỹ sư thực hiện các phép tính quan trọng trong nghiên cứu và phát triển các ứng dụng công nghệ hiện đại.

Khối lượng tuyệt đối của một nguyên tử được xác định bằng cách tính tổng khối lượng của các proton, neutron và electron trong nguyên tử đó. Tuy nhiên, vì khối lượng của electron rất nhỏ nên trong nhiều trường hợp, khối lượng của electron có thể bị bỏ qua để đơn giản hóa phép tính.

Để tính khối lượng tuyệt đối của một nguyên tử, ta sử dụng công thức:

\[
M = (Z \times m_p) + (N \times m_n) + (E \times m_e)
\]

Trong đó:

• \(M\) là khối lượng tuyệt đối của nguyên tử.
• \(Z\) là số proton trong nguyên tử.
• \(m_p\) là khối lượng của một proton, khoảng \[1.6726 \times 10^{-27}\] kg.
• \(N\) là số neutron trong nguyên tử.
• \(m_n\) là khối lượng của một neutron, khoảng \[1.6750 \times 10^{-27}\] kg.
• \(E\) là số electron trong nguyên tử.
• \(m_e\) là khối lượng của một electron, khoảng \[9.109 \times 10^{-31}\] kg.

Với các nguyên tử có số lượng proton và neutron lớn, khối lượng của electron thường rất nhỏ so với tổng khối lượng của proton và neutron. Do đó, công thức có thể được đơn giản hóa thành:

\[
M \approx (Z \times m_p) + (N \times m_n)
\]

Khối lượng tuyệt đối sau khi tính toán có thể được chuyển đổi sang đơn vị khối lượng mol (gram/mol) bằng cách nhân với hằng số Avogadro \(\approx 6.022 \times 10^{23}\) (số lượng nguyên tử trong một mol chất).

Phương pháp tính toán này được sử dụng rộng rãi trong nghiên cứu hóa học và vật lý để xác định chính xác khối lượng của các nguyên tử và phân tử trong các phản ứng và ứng dụng thực tế.

Công thức tính khối lượng tuyệt đối của một nguyên tử không chỉ có ý nghĩa lý thuyết mà còn có nhiều ứng dụng thực tiễn trong nhiều lĩnh vực khoa học và công nghệ. Dưới đây là một số ví dụ về cách công thức này được áp dụng trong thực tế:

• Nghiên cứu hóa học: Việc tính toán khối lượng tuyệt đối của các nguyên tử giúp các nhà khoa học hiểu rõ hơn về tính chất và cấu trúc của các nguyên tố hóa học, từ đó phát triển các chất liệu mới hoặc cải tiến các phương pháp tổng hợp hóa học.
• Công nghệ nano: Trong công nghệ nano, việc xác định khối lượng của các hạt siêu nhỏ là rất quan trọng. Công thức này giúp tính toán khối lượng của từng nguyên tử hoặc phân tử trong các vật liệu nano, đảm bảo tính chính xác trong việc thiết kế và ứng dụng.
• Vật lý hạt nhân: Khối lượng tuyệt đối của nguyên tử được sử dụng để tính toán năng lượng liên kết trong các phản ứng hạt nhân. Điều này giúp dự đoán và kiểm soát các phản ứng xảy ra trong lò phản ứng hạt nhân hoặc trong nghiên cứu vật lý nguyên tử.
• Phát triển dược phẩm: Trong ngành dược phẩm, tính toán khối lượng tuyệt đối của các nguyên tử trong phân tử thuốc giúp tối ưu hóa quá trình thiết kế và tổng hợp các hợp chất dược phẩm mới, đồng thời đảm bảo hiệu quả và an toàn trong sử dụng.
• Giáo dục và đào tạo: Công thức này thường được sử dụng trong giáo dục để giảng dạy các khái niệm cơ bản về vật lý và hóa học, giúp học sinh và sinh viên nắm bắt được cách thức các nguyên tử và phân tử hoạt động và tương tác với nhau.

Nhờ vào những ứng dụng này, công thức tính khối lượng tuyệt đối của nguyên tử không chỉ dừng lại ở lý thuyết mà còn đóng vai trò quan trọng trong việc giải quyết các vấn đề thực tế và thúc đẩy sự tiến bộ trong nhiều ngành khoa học và công nghệ.

Khối lượng tuyệt đối và khối lượng tương đối là hai khái niệm quan trọng trong hóa học và vật lý, giúp mô tả chính xác tính chất của nguyên tử và phân tử. Dưới đây là sự khác biệt và mối quan hệ giữa hai khái niệm này:

• Khối Lượng Tuyệt Đối:

  Khối lượng tuyệt đối của một nguyên tử là khối lượng thực tế của nguyên tử đó, thường được tính bằng đơn vị kilogram (kg). Công thức tính khối lượng tuyệt đối của một nguyên tử thường là:

  \[ m = n \times m_u \]

  Trong đó:

  • \(m\): Khối lượng tuyệt đối của nguyên tử.
  • \(n\): Số mol của nguyên tử.
  • \(m_u\): Khối lượng của một mol nguyên tử, thường được lấy từ bảng tuần hoàn.
• Khối Lượng Tương Đối:

  Khối lượng tương đối, còn gọi là nguyên tử khối hoặc khối lượng nguyên tử, là tỉ số giữa khối lượng của một nguyên tử và khối lượng của một nguyên tử carbon-12. Khối lượng tương đối không có đơn vị và được sử dụng để so sánh khối lượng giữa các nguyên tử với nhau:

  \[ A_r = \frac{m}{m_{C-12}} \]

  Trong đó:

  • \(A_r\): Khối lượng tương đối của nguyên tử.
  • \(m\): Khối lượng tuyệt đối của nguyên tử.
  • \(m_{C-12}\): Khối lượng của một nguyên tử carbon-12.
• Mối Quan Hệ Giữa Khối Lượng Tuyệt Đối Và Khối Lượng Tương Đối:

  Khối lượng tương đối cho phép các nhà khoa học dễ dàng so sánh khối lượng của các nguyên tử mà không cần phải đo lường chúng theo đơn vị tuyệt đối. Trong khi đó, khối lượng tuyệt đối giúp xác định lượng chính xác của các chất trong các phản ứng hóa học. Cả hai khái niệm đều quan trọng và bổ sung cho nhau trong nghiên cứu và ứng dụng thực tiễn.

Khối lượng tuyệt đối của một nguyên tử không chỉ phụ thuộc vào số lượng các proton, neutron và electron trong nguyên tử mà còn bị ảnh hưởng bởi nhiều yếu tố khác. Dưới đây là các yếu tố chính có thể tác động đến khối lượng tuyệt đối:

• Số Proton và Neutron:

  Khối lượng tuyệt đối chủ yếu được xác định bởi số lượng proton và neutron trong hạt nhân. Proton và neutron có khối lượng gần như tương đương, và sự thay đổi số lượng của chúng sẽ làm thay đổi khối lượng tuyệt đối.

• Năng Lượng Liên Kết Hạt Nhân:

  Năng lượng liên kết hạt nhân là năng lượng cần thiết để giữ các proton và neutron lại với nhau trong hạt nhân. Theo thuyết tương đối của Einstein \[E = mc^2\], năng lượng này tương ứng với một khối lượng nhất định và có thể làm giảm khối lượng tuyệt đối của nguyên tử.

• Đồng Vị:

  Các đồng vị của một nguyên tố có cùng số proton nhưng khác số neutron. Do đó, chúng có khối lượng tuyệt đối khác nhau. Việc phân bố đồng vị trong tự nhiên ảnh hưởng đến khối lượng trung bình của nguyên tố đó.

• Hiệu Ứng Môi Trường:

  Môi trường xung quanh nguyên tử, bao gồm áp suất, nhiệt độ, và từ trường, có thể ảnh hưởng nhỏ đến khối lượng tuyệt đối, đặc biệt là ở các điều kiện cực đoan.

Việc hiểu rõ các yếu tố này giúp các nhà khoa học có thể tính toán và ứng dụng khối lượng tuyệt đối của nguyên tử trong nghiên cứu và công nghệ một cách chính xác hơn.

Khối lượng tuyệt đối của nguyên tử đóng vai trò quan trọng trong nhiều lĩnh vực nghiên cứu khoa học, đặc biệt là trong hóa học và vật lý. Việc xác định chính xác khối lượng này giúp các nhà khoa học hiểu rõ hơn về cấu trúc vi mô của vật chất và các hiện tượng tự nhiên.

Một số ứng dụng tiêu biểu của khối lượng tuyệt đối trong nghiên cứu khoa học bao gồm:

• Xác định thành phần nguyên tử: Khối lượng tuyệt đối giúp tính toán và xác định số lượng các hạt cơ bản như proton, neutron trong một nguyên tử.
• Nghiên cứu phản ứng hạt nhân: Khối lượng tuyệt đối được sử dụng để tính toán năng lượng giải phóng hoặc hấp thụ trong các phản ứng hạt nhân, từ đó giúp phát triển công nghệ hạt nhân.
• Đo lường và phân tích vật liệu: Các phép đo khối lượng tuyệt đối hỗ trợ trong việc xác định tính chất vật lý của vật liệu, từ đó phục vụ cho việc phát triển các sản phẩm công nghệ cao.

Trong nghiên cứu, việc sử dụng đơn vị khối lượng tuyệt đối \(\text{kg}\) hoặc đơn vị khối lượng nguyên tử (amu) \(\left( \text{1 amu} = 1,661 \times 10^{-27} \text{ kg} \right)\) là cực kỳ quan trọng để đảm bảo độ chính xác trong các phép tính và thí nghiệm.

Nhìn chung, khối lượng tuyệt đối không chỉ là một chỉ số cơ bản mà còn là công cụ hỗ trợ quan trọng trong nhiều lĩnh vực khoa học khác nhau, giúp con người hiểu sâu hơn về thế giới vi mô.

Khối lượng tuyệt đối của một nguyên tử là một yếu tố cơ bản trong việc hiểu rõ bản chất của vật chất và các phản ứng vi mô. Việc nắm vững cách tính khối lượng này không chỉ giúp trong các nghiên cứu khoa học mà còn ứng dụng rộng rãi trong nhiều lĩnh vực khác như công nghệ, y học, và giáo dục.

Qua các phần trên, chúng ta đã tìm hiểu về khối lượng tuyệt đối, từ khái niệm, công thức tính toán cho đến các ứng dụng trong thực tế và nghiên cứu khoa học. Hy vọng rằng, bài viết này đã cung cấp cho bạn một cái nhìn toàn diện và hữu ích về khối lượng tuyệt đối của nguyên tử.

Trong tương lai, với sự tiến bộ không ngừng của khoa học và công nghệ, những kiến thức này sẽ tiếp tục được mở rộng và ứng dụng vào nhiều lĩnh vực mới, đóng góp vào sự phát triển bền vững của nhân loại.