Chủ đề biểu thức tính cảm ứng từ: Biểu thức tính cảm ứng từ là một chủ đề quan trọng trong vật lý, đóng vai trò then chốt trong việc hiểu các hiện tượng từ trường và ứng dụng trong đời sống. Bài viết này sẽ cung cấp hướng dẫn chi tiết và các ứng dụng thực tế của biểu thức này, giúp bạn nắm vững kiến thức và áp dụng hiệu quả vào các tình huống cụ thể.
Mục lục
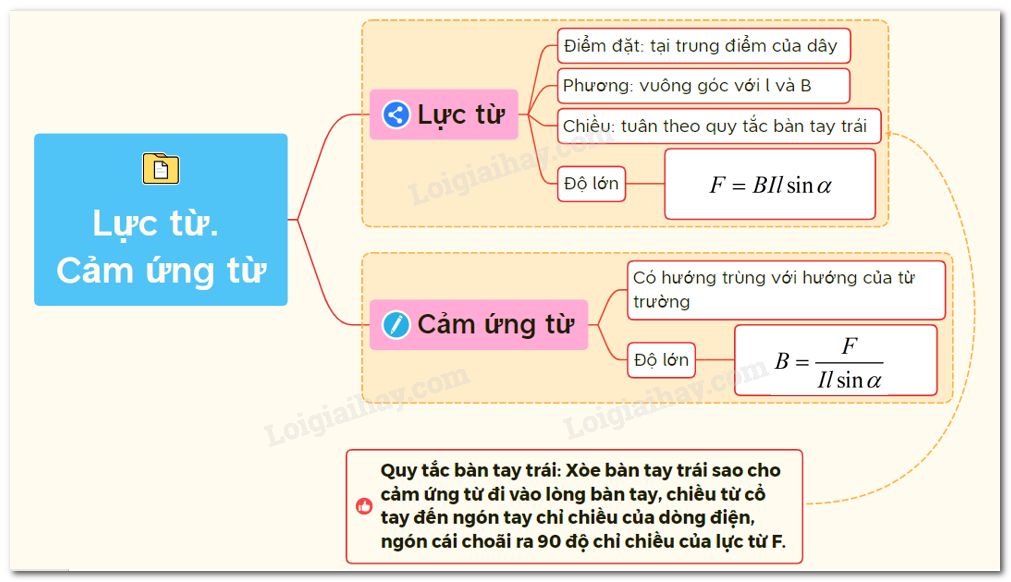
Biểu Thức Tính Cảm Ứng Từ
Trong vật lý, cảm ứng từ là một đại lượng quan trọng trong việc mô tả từ trường tại một điểm trong không gian xung quanh dòng điện. Dưới đây là các công thức cơ bản và các ứng dụng thực tế của cảm ứng từ:
1. Công Thức Tính Cảm Ứng Từ
- Đối với dây dẫn thẳng dài:
- \(\mu_0\) là hằng số từ thẩm trong chân không (\(\mu_0 = 4\pi \times 10^{-7} \, T\cdot m/A\)).
- \(I\) là cường độ dòng điện (đơn vị: Ampe).
- \(r\) là khoảng cách từ điểm cần tính đến dây dẫn (đơn vị: mét).
- Đối với vòng dây tròn:
- \(R\) là bán kính của vòng dây (đơn vị: mét).
- \(I\) là cường độ dòng điện chạy qua vòng dây.
- Đối với ống dây dẫn:
- \(n\) là số vòng dây trên một đơn vị độ dài ống dây (đơn vị: vòng/mét).
- \(L\) là chiều dài của ống dây (đơn vị: mét).
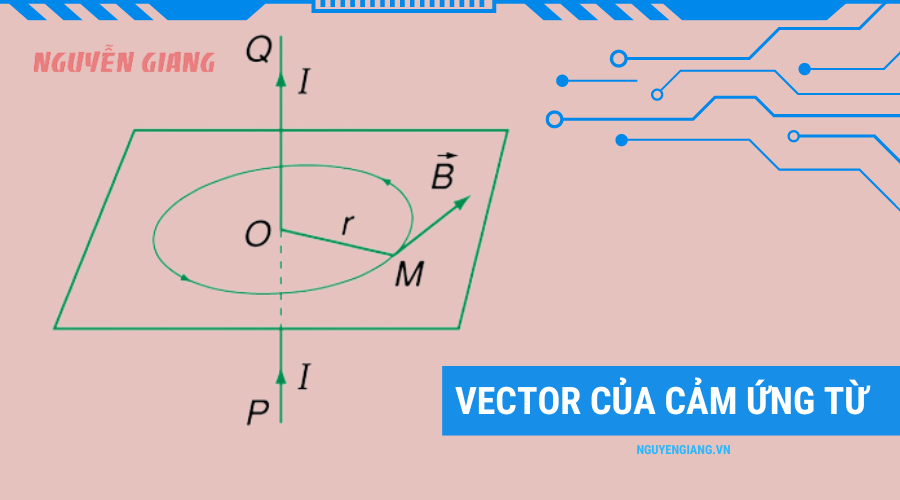
Giả sử có một dây dẫn thẳng dài vô hạn mang dòng điện \(I\). Cảm ứng từ \(B\) tại một điểm cách dây dẫn một khoảng \(r\) được tính theo công thức:
\[ B = \frac{\mu_0 I}{2 \pi r} \]Trong đó:
Giả sử có một vòng dây tròn bán kính \(R\) mang dòng điện \(I\). Cảm ứng từ \(B\) tại tâm của vòng dây được tính bằng:
\[ B = \frac{2\pi \times 10^{-7} \cdot I}{R} \]Trong đó:
Cảm ứng từ \(B\) tại một điểm bên trong lòng ống dây có chiều dài \(L\), số vòng dây \(N\), và cường độ dòng điện \(I\) được xác định bởi:
\[ B = \frac{4\pi \times 10^{-7} \cdot I \cdot N}{L} = 4\pi \times 10^{-7} \cdot n \cdot I \]Trong đó:
2. Ứng Dụng Của Cảm Ứng Từ
Cảm ứng từ có nhiều ứng dụng thực tiễn trong đời sống và công nghiệp, bao gồm:
- Bếp từ: Sử dụng cảm ứng từ để tạo ra nhiệt trực tiếp trên đáy nồi, giúp nấu ăn hiệu quả và tiết kiệm năng lượng.
- Đèn huỳnh quang: Nguyên lý cảm ứng từ giúp tạo ra điện áp cao, kích thích các ion phát sáng, làm đèn hoạt động hiệu quả.
- Động cơ điện: Cảm ứng từ giúp tạo ra chuyển động quay trong các thiết bị như quạt điện, máy bơm, và máy phát điện.
- Máy phát điện: Cảm ứng từ được sử dụng để biến đổi năng lượng cơ học thành điện năng.
- Y học: Chụp cộng hưởng từ (MRI) sử dụng nguyên lý cảm ứng từ để tạo ra hình ảnh chi tiết của cơ thể, hỗ trợ chẩn đoán và điều trị.
Như vậy, việc hiểu rõ các công thức tính cảm ứng từ không chỉ giúp chúng ta nắm vững kiến thức vật lý mà còn ứng dụng hiệu quả trong nhiều lĩnh vực khác nhau.
.png)
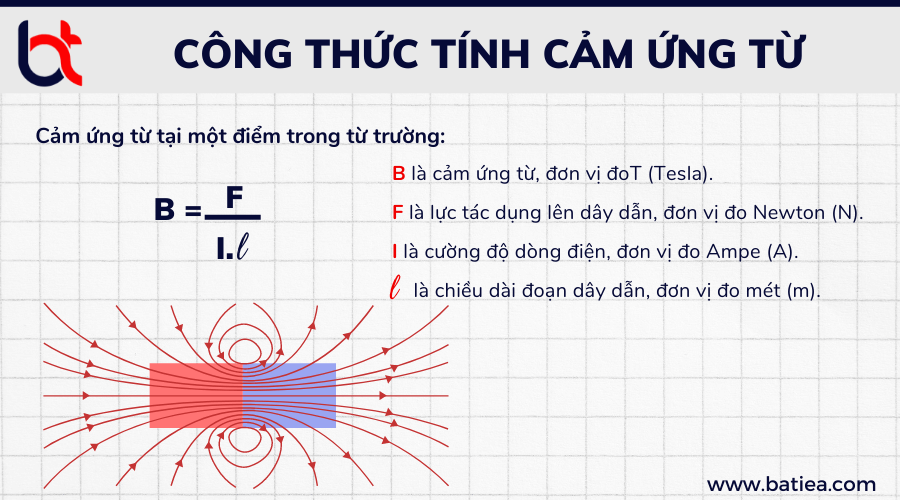
1. Khái Niệm Cơ Bản về Cảm Ứng Từ
Cảm ứng từ, ký hiệu là \( \mathbf{B} \), là một đại lượng vật lý biểu thị độ mạnh của từ trường tại một điểm nhất định trong không gian. Từ trường được sinh ra bởi các hạt mang điện chuyển động, và cảm ứng từ là yếu tố cho biết mức độ ảnh hưởng của từ trường lên các hạt khác.
Từ trường có thể được sinh ra bởi dòng điện chạy qua một dây dẫn hoặc bởi các nam châm. Cảm ứng từ được đo bằng đơn vị Tesla (T) trong hệ đo lường quốc tế. Công thức cơ bản để tính cảm ứng từ tại một điểm trong không gian do một dòng điện thẳng dài sinh ra là:
\[
B = \frac{\mu_0 \cdot I}{2\pi r}
\]
Trong đó:
- \(B\) là cảm ứng từ (Tesla, T)
- \(\mu_0\) là hằng số từ (4π × 10-7 T·m/A)
- \(I\) là cường độ dòng điện (A)
- \(r\) là khoảng cách từ điểm xét đến dây dẫn (m)
Cảm ứng từ không chỉ phụ thuộc vào cường độ dòng điện và khoảng cách từ nguồn mà còn phụ thuộc vào môi trường từ trường. Trong một môi trường đồng nhất và không có từ tính đặc biệt, công thức trên có thể được áp dụng một cách đơn giản và trực tiếp.
Tuy nhiên, đối với các hình dạng phức tạp của dây dẫn hoặc các trường hợp có sự hiện diện của nhiều nguồn từ trường, việc tính toán cảm ứng từ sẽ trở nên phức tạp hơn. Khi đó, cần sử dụng nguyên lý chồng chất từ trường, trong đó tổng cảm ứng từ tại một điểm là tổng vector của các cảm ứng từ do từng nguồn sinh ra.
2. Các Công Thức Tính Cảm Ứng Từ
Cảm ứng từ là một đại lượng quan trọng trong từ trường, và các công thức tính cảm ứng từ được sử dụng để xác định độ lớn của từ trường trong các tình huống khác nhau. Dưới đây là một số công thức cơ bản và quan trọng nhất:
2.1. Công Thức Tính Cảm Ứng Từ cho Dòng Điện Thẳng Dài
Khi dòng điện chạy qua một dây dẫn thẳng dài vô hạn, cảm ứng từ tại một điểm cách dây một khoảng \( r \) được tính bằng công thức:
\[
B = \frac{\mu_0 \cdot I}{2\pi r}
\]
- \(B\) là cảm ứng từ tại điểm xét (Tesla, T)
- \(\mu_0\) là hằng số từ (4π × 10-7 T·m/A)
- \(I\) là cường độ dòng điện (Ampe, A)
- \(r\) là khoảng cách từ điểm xét đến dây dẫn (m)
2.2. Công Thức Tính Cảm Ứng Từ trong Vòng Dây Tròn
Đối với một vòng dây dẫn tròn, cảm ứng từ tại tâm của vòng dây được xác định bằng công thức:
\[
B = \frac{\mu_0 \cdot I \cdot N}{2R}
\]
- \(N\) là số vòng dây
- \(R\) là bán kính của vòng dây (m)
2.3. Công Thức Tính Cảm Ứng Từ trong Ống Dây Solenoid
Trong trường hợp của ống dây solenoid (ống dây dài với nhiều vòng dây), cảm ứng từ bên trong ống dây được tính bằng công thức:
\[
B = \mu_0 \cdot n \cdot I
\]
- \(n\) là mật độ vòng dây, tức là số vòng dây trên một đơn vị chiều dài của ống (vòng/m)
2.4. Nguyên Lý Chồng Chất Từ Trường
Khi có nhiều nguồn từ trường khác nhau cùng tác động tại một điểm, cảm ứng từ tổng hợp tại điểm đó được xác định bằng tổng vector của các cảm ứng từ do từng nguồn sinh ra:
\[
\mathbf{B}_{\text{tổng}} = \mathbf{B}_1 + \mathbf{B}_2 + \dots + \mathbf{B}_n
\]
Trong đó, mỗi \( \mathbf{B}_i \) là cảm ứng từ do nguồn thứ \( i \) gây ra.
Các công thức trên là cơ sở để tính toán cảm ứng từ trong nhiều bài toán thực tế, giúp chúng ta hiểu rõ hơn về sự tương tác của từ trường với các vật thể và dòng điện.

3. Ứng Dụng của Cảm Ứng Từ trong Thực Tế
Cảm ứng từ có nhiều ứng dụng quan trọng trong cuộc sống hàng ngày cũng như trong các ngành công nghiệp hiện đại. Dưới đây là một số ứng dụng phổ biến và quan trọng của hiện tượng cảm ứng từ:
3.1. Ứng Dụng trong Máy Phát Điện
Máy phát điện hoạt động dựa trên nguyên lý cảm ứng từ, trong đó từ trường biến thiên tạo ra dòng điện. Khi cuộn dây quay trong một từ trường hoặc từ trường thay đổi xung quanh cuộn dây, sẽ xuất hiện một suất điện động cảm ứng, từ đó sinh ra dòng điện xoay chiều phục vụ nhu cầu tiêu dùng.
3.2. Ứng Dụng trong Động Cơ Điện
Trong động cơ điện, cảm ứng từ được sử dụng để chuyển đổi năng lượng điện thành năng lượng cơ học. Khi dòng điện chạy qua cuộn dây trong từ trường, một lực điện từ sẽ được sinh ra, làm cho rotor quay. Đây là nguyên lý cơ bản của các động cơ trong các thiết bị gia dụng và phương tiện vận tải.
3.3. Ứng Dụng trong Tàu Đệm Từ
Tàu đệm từ là một hệ thống giao thông hiện đại, sử dụng từ trường mạnh để nâng và đẩy tàu chạy với tốc độ cao mà không cần tiếp xúc với đường ray. Nhờ vào cảm ứng từ, tàu có thể di chuyển êm ái và nhanh chóng, giảm thiểu ma sát và tiết kiệm năng lượng.
3.4. Ứng Dụng trong Y Tế
Cảm ứng từ cũng có vai trò quan trọng trong y tế, đặc biệt là trong máy MRI (chụp cộng hưởng từ). Thiết bị này sử dụng từ trường mạnh để tạo ra hình ảnh chi tiết của các mô bên trong cơ thể, giúp các bác sĩ chẩn đoán bệnh lý một cách chính xác mà không cần xâm lấn.
3.5. Ứng Dụng trong Cảm Biến Từ
Cảm biến từ được sử dụng rộng rãi trong công nghiệp để phát hiện và đo lường các vật thể từ tính. Chúng được sử dụng trong tự động hóa, kiểm soát chất lượng và nhiều quy trình công nghệ khác, đảm bảo sự chính xác và hiệu quả trong sản xuất.
Những ứng dụng trên chỉ là một phần nhỏ trong số rất nhiều ứng dụng khác của cảm ứng từ. Nó không chỉ là một khái niệm lý thuyết mà còn là nền tảng cho nhiều công nghệ hiện đại, góp phần quan trọng vào sự phát triển của xã hội.

XEM THÊM:
4. Các Bài Tập Thực Hành về Cảm Ứng Từ
Để hiểu rõ hơn về cảm ứng từ và các công thức liên quan, việc thực hành qua các bài tập là rất cần thiết. Dưới đây là một số bài tập giúp bạn củng cố kiến thức và áp dụng lý thuyết vào thực tế.
4.1. Bài Tập 1: Tính Toán Cảm Ứng Từ của Dòng Điện Thẳng Dài
Giả sử có một dòng điện cường độ \( I = 5 \, A \) chạy qua một dây dẫn thẳng dài. Tính cảm ứng từ tại một điểm cách dây dẫn \( r = 2 \, cm \).
Bài giải:
Áp dụng công thức:
\[
B = \frac{\mu_0 \cdot I}{2\pi r}
\]
với \( \mu_0 = 4\pi \times 10^{-7} \, T \cdot m/A \), ta có:
\[
B = \frac{4\pi \times 10^{-7} \times 5}{2\pi \times 0.02} \, T = 5 \times 10^{-5} \, T
\]
4.2. Bài Tập 2: Cảm Ứng Từ trong Vòng Dây Tròn
Một vòng dây tròn có bán kính \( R = 10 \, cm \) và mang dòng điện \( I = 3 \, A \). Tính cảm ứng từ tại tâm của vòng dây.
Bài giải:
Sử dụng công thức:
\[
B = \frac{\mu_0 \cdot I}{2R}
\]
với \( R = 0.1 \, m \), ta có:
\[
B = \frac{4\pi \times 10^{-7} \times 3}{2 \times 0.1} \, T = 1.88 \times 10^{-5} \, T
\]
4.3. Bài Tập 3: Cảm Ứng Từ trong Ống Dây Solenoid
Cho một ống dây solenoid dài có mật độ vòng dây \( n = 1000 \, vòng/m \) và cường độ dòng điện \( I = 2 \, A \). Tính cảm ứng từ bên trong ống dây.
Bài giải:
Dùng công thức:
\[
B = \mu_0 \cdot n \cdot I
\]
ta tính được:
\[
B = 4\pi \times 10^{-7} \times 1000 \times 2 \, T = 2.51 \times 10^{-3} \, T
\]
Các bài tập trên không chỉ giúp bạn hiểu rõ hơn về lý thuyết mà còn nâng cao kỹ năng giải quyết các bài toán về cảm ứng từ. Hãy thực hành nhiều hơn để nắm vững kiến thức này!

5. Kết Luận và Tổng Kết
Qua các phần đã trình bày, chúng ta đã cùng tìm hiểu sâu về cảm ứng từ, từ khái niệm cơ bản, các công thức tính toán đến những ứng dụng thực tế trong đời sống và công nghiệp. Cảm ứng từ không chỉ là một khái niệm quan trọng trong lý thuyết vật lý mà còn là nền tảng cho nhiều công nghệ hiện đại.
Các công thức tính cảm ứng từ giúp chúng ta dễ dàng xác định độ lớn của từ trường trong nhiều tình huống khác nhau, từ dòng điện thẳng dài, vòng dây tròn đến ống dây solenoid. Những ứng dụng của cảm ứng từ cũng được thể hiện rõ qua việc vận hành các thiết bị như máy phát điện, động cơ điện, và cả trong y tế với máy MRI.
Những bài tập thực hành được đưa ra nhằm củng cố kiến thức và giúp bạn áp dụng các công thức vào thực tế một cách hiệu quả. Việc hiểu rõ và thành thạo cảm ứng từ sẽ mở ra nhiều cơ hội trong nghiên cứu khoa học cũng như trong công nghệ ứng dụng.
Như vậy, cảm ứng từ là một khía cạnh không thể thiếu trong khoa học vật lý, và việc nắm vững kiến thức về nó sẽ giúp chúng ta hiểu sâu hơn về các hiện tượng từ trường và ứng dụng chúng vào đời sống. Hy vọng rằng bài viết này đã mang lại cho bạn những kiến thức cần thiết và hữu ích.