Chủ đề ban đầu có 5g chất phóng xạ radon: Ban đầu có 5g chất phóng xạ Radon là một khởi đầu quan trọng trong nhiều bài toán liên quan đến chu kỳ bán rã. Bài viết này sẽ khám phá sâu về Radon, cách tính toán số nguyên tử còn lại sau thời gian nhất định và các ứng dụng thực tế của chất phóng xạ này.
Mục lục
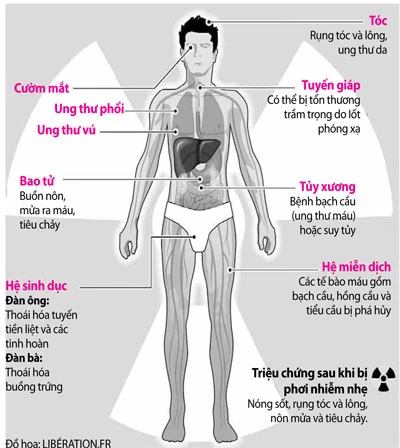
Radon nguy hiểm như thế nào?
Radon là một chất khí phóng xạ tự nhiên không màu, không mùi, và không vị. Mặc dù radon tồn tại ở mức độ thấp trong không khí xung quanh, nhưng khi nó tích tụ trong không gian kín, như trong nhà, nồng độ có thể tăng cao và gây nguy hiểm cho sức khỏe con người.
1. Nguy cơ ung thư phổi
Mối nguy hiểm lớn nhất của radon là nguy cơ gây ung thư phổi. Theo Tổ chức Y tế Thế giới (WHO) và Cơ quan Bảo vệ Môi trường Hoa Kỳ (EPA), radon là nguyên nhân hàng đầu gây ung thư phổi ở những người không hút thuốc, và chỉ đứng sau thuốc lá đối với những người hút thuốc. Các nghiên cứu đã chỉ ra rằng phơi nhiễm radon lâu dài có thể dẫn đến đột biến trong tế bào phổi, dẫn đến ung thư.
2. Quá trình phơi nhiễm radon
Radon xâm nhập vào cơ thể chủ yếu qua đường hô hấp. Khi hít thở không khí chứa radon, các hạt phóng xạ sẽ bám vào niêm mạc phổi, phát ra bức xạ và gây tổn thương DNA trong tế bào phổi. Quá trình này diễn ra âm thầm và có thể kéo dài nhiều năm trước khi các triệu chứng ung thư phổi xuất hiện.
3. Các triệu chứng liên quan
Các triệu chứng ung thư phổi do phơi nhiễm radon thường không rõ ràng ở giai đoạn đầu. Khi bệnh tiến triển, có thể xuất hiện các triệu chứng như:
- Ho kéo dài
- Khó thở
- Đau ngực
- Ho ra máu
- Giảm cân không rõ lý do
4. Đánh giá nguy cơ
Nguy cơ mắc ung thư phổi do radon phụ thuộc vào nồng độ radon trong không khí và thời gian phơi nhiễm. Những người sống trong môi trường có nồng độ radon cao trong nhiều năm có nguy cơ cao hơn. Nguy cơ cũng tăng lên đáng kể đối với những người hút thuốc.
Kết luận
Radon là một chất nguy hiểm đối với sức khỏe, đặc biệt là trong các không gian kín như nhà ở. Việc kiểm tra và giảm thiểu radon là cần thiết để bảo vệ sức khỏe, đặc biệt là để ngăn ngừa nguy cơ ung thư phổi.

.png)
1. Giới thiệu về chất phóng xạ Radon
Radon (ký hiệu hóa học: Rn) là một nguyên tố hóa học thuộc nhóm khí hiếm, không màu, không mùi và không vị. Đây là một chất phóng xạ tự nhiên được sinh ra từ sự phân rã của Uranium và Thorium trong lòng đất. Radon có chu kỳ bán rã là 3,8 ngày, tức là sau khoảng thời gian này, một nửa lượng Radon sẽ bị phân rã thành các nguyên tố khác.
Radon tồn tại ở trạng thái khí trong điều kiện thường và có khả năng thâm nhập vào không khí từ các vật liệu xây dựng, đất đai và nước ngầm. Khi radon phân rã, nó sinh ra các hạt phóng xạ alpha, có thể gây hại cho sức khỏe nếu hít phải trong thời gian dài. Điều này khiến Radon trở thành một yếu tố quan trọng cần được quản lý trong các ngôi nhà và công trình xây dựng.
Công thức phân rã của Radon có thể được mô tả bằng phương trình toán học sau:
\[ N(t) = N_0 \times \left( \frac{1}{2} \right)^{\frac{t}{T}} \]
- \(N(t)\): Số nguyên tử Radon còn lại sau thời gian \(t\)
- \(N_0\): Số nguyên tử Radon ban đầu
- \(T\): Chu kỳ bán rã (3,8 ngày đối với Radon)
Radon được tìm thấy ở nhiều nơi trên thế giới và có thể tích tụ trong nhà ở hoặc các tòa nhà kín gió. Do đó, việc kiểm tra và giảm thiểu nồng độ Radon trong không khí là rất cần thiết để bảo vệ sức khỏe con người.
2. Tính toán liên quan đến chất phóng xạ Radon
Việc tính toán liên quan đến chất phóng xạ Radon thường xoay quanh quá trình phân rã của nó, đặc biệt là việc xác định khối lượng hoặc số nguyên tử còn lại sau một khoảng thời gian nhất định. Dưới đây là các bước cơ bản để thực hiện các phép tính liên quan đến Radon.
2.1. Công thức tính số nguyên tử hoặc khối lượng còn lại
Radon có chu kỳ bán rã \(T = 3,8\) ngày. Công thức tính số nguyên tử hoặc khối lượng Radon còn lại sau thời gian \(t\) ngày được biểu diễn như sau:
\[ N(t) = N_0 \times \left( \frac{1}{2} \right)^{\frac{t}{T}} \]
Trong đó:
- \(N(t)\): Số nguyên tử hoặc khối lượng Radon còn lại sau thời gian \(t\).
- \(N_0\): Số nguyên tử hoặc khối lượng Radon ban đầu.
- \(T\): Chu kỳ bán rã (đối với Radon là 3,8 ngày).
2.2. Ví dụ minh họa
Giả sử ban đầu có 5g chất phóng xạ Radon. Chúng ta cần tính khối lượng Radon còn lại sau \(t = 9,5\) ngày:
\[ N(9,5) = 5 \times \left( \frac{1}{2} \right)^{\frac{9,5}{3,8}} \approx 1,25 \, \text{g} \]
Sau 9,5 ngày, khối lượng Radon còn lại xấp xỉ 1,25g.
2.3. Bảng tính khối lượng Radon còn lại theo thời gian
| Thời gian (ngày) | Khối lượng còn lại (g) |
| 0 | 5,00 |
| 3,8 | 2,50 |
| 7,6 | 1,25 |
| 9,5 | 1,25 |
Qua bảng tính trên, có thể thấy rằng sau mỗi chu kỳ bán rã, khối lượng chất phóng xạ giảm đi một nửa, minh họa rõ ràng quá trình phân rã phóng xạ của Radon.

3. Ví dụ về bài toán với 5g chất phóng xạ Radon
Để minh họa cho cách tính toán liên quan đến chất phóng xạ Radon, chúng ta hãy xét một ví dụ cụ thể như sau:
3.1 Bài toán về chu kỳ bán rã 3,8 ngày
Giả sử ban đầu có 5g chất phóng xạ Radon \( ^{222}_{86}Rn \) với chu kỳ bán rã là 3,8 ngày. Chúng ta cần tính khối lượng chất Radon còn lại sau một khoảng thời gian nhất định.
Bài toán: Tính khối lượng chất Radon còn lại sau 9,5 ngày.
3.2 Cách giải bài toán với số liệu cụ thể
- Xác định số chu kỳ bán rã đã trải qua:
Thời gian đã trôi qua là 9,5 ngày. Số chu kỳ bán rã \( n \) được tính theo công thức:
\[ n = \frac{t}{T_{1/2}} \]Trong đó \( t = 9,5 \) ngày và \( T_{1/2} = 3,8 \) ngày.
\[ n = \frac{9,5}{3,8} \approx 2,5 \] - Tính phần còn lại của chất phóng xạ:
Sau mỗi chu kỳ bán rã, khối lượng chất phóng xạ giảm đi một nửa. Do đó, khối lượng còn lại sau 9,5 ngày được tính bằng công thức:
\[ m = m_0 \times \left(\frac{1}{2}\right)^n \]Với \( m_0 = 5 \)g là khối lượng ban đầu và \( n = 2,5 \) là số chu kỳ bán rã đã trải qua.
\[ m = 5 \times \left(\frac{1}{2}\right)^{2,5} \approx 5 \times 0,1768 \approx 0,884g \]Vậy, sau 9,5 ngày, khối lượng chất phóng xạ Radon còn lại là khoảng 0,884g.
Bài toán này minh họa cách sử dụng chu kỳ bán rã để tính khối lượng còn lại của chất phóng xạ sau một khoảng thời gian cụ thể. Đây là một công cụ quan trọng trong việc nghiên cứu và ứng dụng các chất phóng xạ trong thực tế.

4. Các dạng bài tập liên quan đến Radon
Dưới đây là một số dạng bài tập liên quan đến chất phóng xạ Radon, giúp học sinh hiểu rõ hơn về các hiện tượng phóng xạ và cách tính toán trong thực tế:
4.1 Bài tập tính khối lượng chất còn lại sau một khoảng thời gian
Dạng bài tập này yêu cầu tính toán khối lượng chất phóng xạ Radon còn lại sau một khoảng thời gian nhất định. Để giải quyết bài toán, chúng ta sử dụng công thức phân rã phóng xạ:
\[ m(t) = m_0 \times \left(\frac{1}{2}\right)^{\frac{t}{T_{1/2}}} \]
Trong đó:
- \( m(t) \) là khối lượng chất phóng xạ còn lại sau thời gian \( t \).
- \( m_0 \) là khối lượng ban đầu của chất phóng xạ (5g trong ví dụ này).
- \( T_{1/2} \) là chu kỳ bán rã của chất phóng xạ Radon (3,8 ngày).
- \( t \) là thời gian đã trôi qua.
Ví dụ: Tính khối lượng Radon còn lại sau 9,5 ngày.
Áp dụng công thức:
\[ m(9.5) = 5 \times \left(\frac{1}{2}\right)^{\frac{9.5}{3.8}} \approx 1.25 \, \text{g} \]
Vậy sau 9,5 ngày, khối lượng Radon còn lại xấp xỉ 1,25g.
4.2 Bài tập tính số nguyên tử sau một chu kỳ bán rã
Ở dạng bài tập này, mục tiêu là xác định số nguyên tử Radon còn lại sau một hoặc nhiều chu kỳ bán rã. Số nguyên tử còn lại có thể được tính bằng cách sử dụng công thức:
\[ N(t) = N_0 \times \left(\frac{1}{2}\right)^{\frac{t}{T_{1/2}}} \]
Trong đó:
- \( N(t) \) là số nguyên tử còn lại sau thời gian \( t \).
- \( N_0 \) là số nguyên tử ban đầu.
Ví dụ: Nếu ban đầu có \( 6.02 \times 10^{23} \) nguyên tử Radon, tính số nguyên tử còn lại sau 7,6 ngày (tương đương 2 chu kỳ bán rã).
Áp dụng công thức:
\[ N(7.6) = 6.02 \times 10^{23} \times \left(\frac{1}{2}\right)^{\frac{7.6}{3.8}} \approx 1.505 \times 10^{23} \, \text{nguyên tử} \]
Vậy sau 7,6 ngày, số nguyên tử Radon còn lại xấp xỉ \( 1.505 \times 10^{23} \) nguyên tử.
4.3 Bài tập ứng dụng thực tế về phóng xạ Radon
Dạng bài tập này yêu cầu áp dụng kiến thức về phóng xạ Radon vào các tình huống thực tế, chẳng hạn như tính toán liều lượng phóng xạ trong môi trường sống, hoặc đánh giá rủi ro phơi nhiễm Radon trong nhà ở.
Ví dụ: Một ngôi nhà có nồng độ Radon trong không khí là 200 Bq/m³. Tính liều lượng phơi nhiễm Radon trong một năm cho người sống trong nhà.
Giả sử người đó hít thở 20 m³ không khí mỗi ngày và hít thở 365 ngày trong một năm:
\[ \text{Liều lượng phơi nhiễm} = 200 \times 20 \times 365 \, \text{Bq} \approx 1,46 \times 10^6 \, \text{Bq/năm} \]
Với kết quả này, người dùng có thể đánh giá mức độ nguy hiểm và áp dụng các biện pháp giảm thiểu rủi ro.
Các bài tập này giúp học sinh không chỉ rèn luyện kỹ năng tính toán mà còn hiểu rõ hơn về tác động của phóng xạ trong đời sống và các biện pháp bảo vệ sức khỏe.