Chủ đề ban đầu có 20g chất phóng xạ x: Bài viết này sẽ giúp bạn hiểu rõ về quá trình phân rã của 20g chất phóng xạ X, cách tính toán khối lượng còn lại sau các chu kỳ bán rã, cùng với các ứng dụng thực tiễn trong y học, công nghiệp và nghiên cứu khoa học. Những ví dụ và bài tập minh họa sẽ giúp bạn nắm vững kiến thức quan trọng này.
Mục lục
Ứng Dụng Của Chất Phóng Xạ X
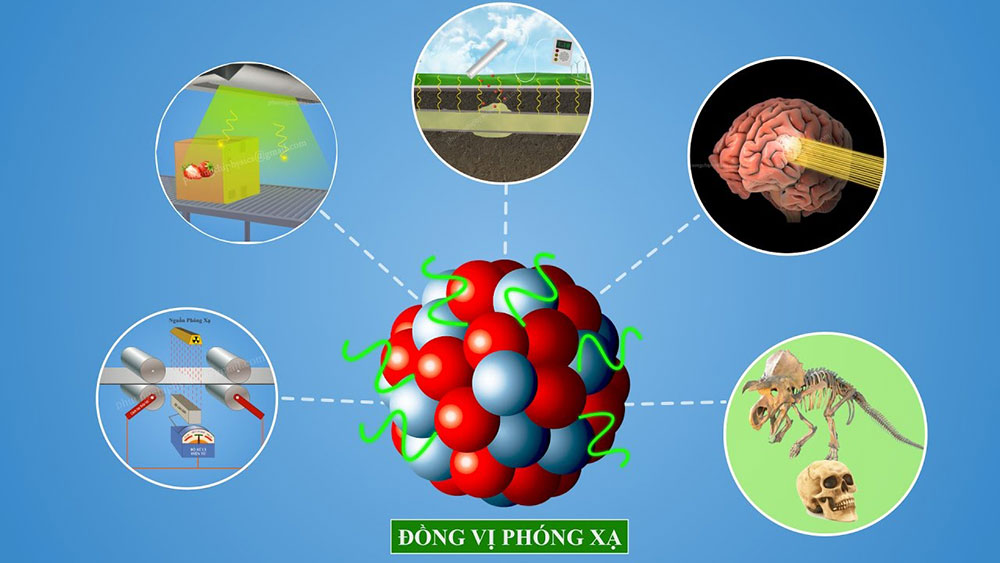
Chất phóng xạ X thường được sử dụng trong nhiều lĩnh vực quan trọng như y học, công nghiệp, và nghiên cứu khoa học. Dưới đây là một số ứng dụng phổ biến:
1. Trong Y Học
- Sử dụng trong xạ trị để điều trị các loại ung thư. Chất phóng xạ có thể nhắm mục tiêu vào các tế bào ung thư và tiêu diệt chúng mà không gây tổn hại quá nhiều đến các tế bào khỏe mạnh xung quanh.
- Chẩn đoán hình ảnh: Chất phóng xạ được dùng trong các kỹ thuật hình ảnh như PET scan và SPECT để phát hiện sớm các vấn đề y tế.
2. Trong Công Nghiệp
- Kiểm tra chất lượng vật liệu: Chất phóng xạ X được sử dụng để kiểm tra cấu trúc bên trong của các vật liệu mà không cần phá hủy chúng.
- Sử dụng trong việc đo lường độ dày của các lớp vật liệu trong quá trình sản xuất.
3. Trong Nghiên Cứu Khoa Học
- Chất phóng xạ X được sử dụng để nghiên cứu các quá trình phân rã hạt nhân và các phản ứng hạt nhân khác.
- Đánh dấu các phân tử để theo dõi các quá trình sinh học trong nghiên cứu y sinh.
4. Tính Toán Thời Gian Phân Rã
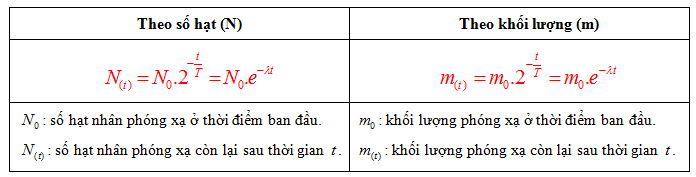
Giả sử ban đầu có \(20 \, \text{g}\) chất phóng xạ X với chu kỳ bán rã là \(T\). Khối lượng chất phóng xạ X còn lại sau khoảng thời gian \(3T\) được tính bằng công thức:
Với \(t = 3T\) và \(m_0 = 20 \, \text{g}\):
Do đó, sau 3 chu kỳ bán rã, khối lượng chất X còn lại là \(2.5 \, \text{g}\).

.png)
1. Giới thiệu về chất phóng xạ X và các ứng dụng
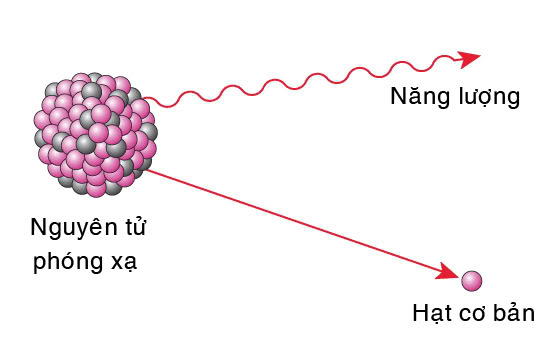
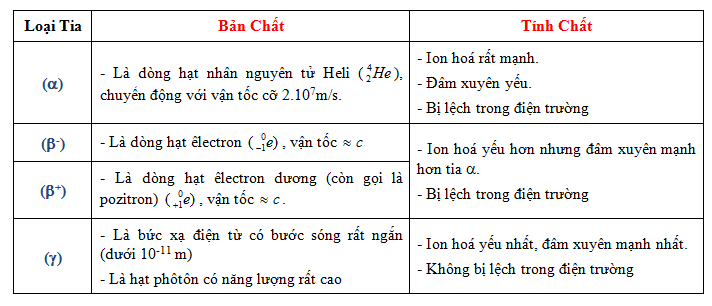
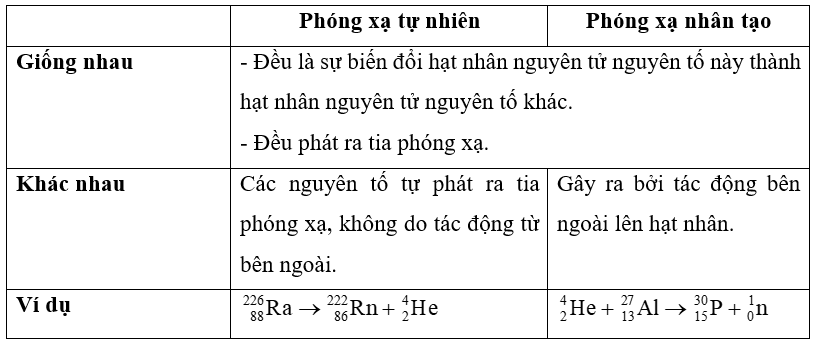
Chất phóng xạ X là một dạng chất có khả năng phát ra các tia bức xạ do sự phân rã của các hạt nhân không ổn định trong chất đó. Quá trình phân rã này xảy ra tự nhiên và được định nghĩa bởi chu kỳ bán rã, là khoảng thời gian cần để một nửa lượng chất phóng xạ ban đầu phân rã.
Chất phóng xạ X có nhiều ứng dụng quan trọng trong cuộc sống. Trong y học, nó được sử dụng trong chẩn đoán và điều trị các bệnh như ung thư thông qua kỹ thuật xạ trị. Ngoài ra, trong công nghiệp, chất phóng xạ X đóng vai trò quan trọng trong việc kiểm tra chất lượng vật liệu và sản phẩm. Chất phóng xạ X cũng được sử dụng rộng rãi trong nghiên cứu khoa học để tìm hiểu về các hiện tượng vật lý và sinh học, cung cấp thông tin quý giá cho sự phát triển khoa học và công nghệ.
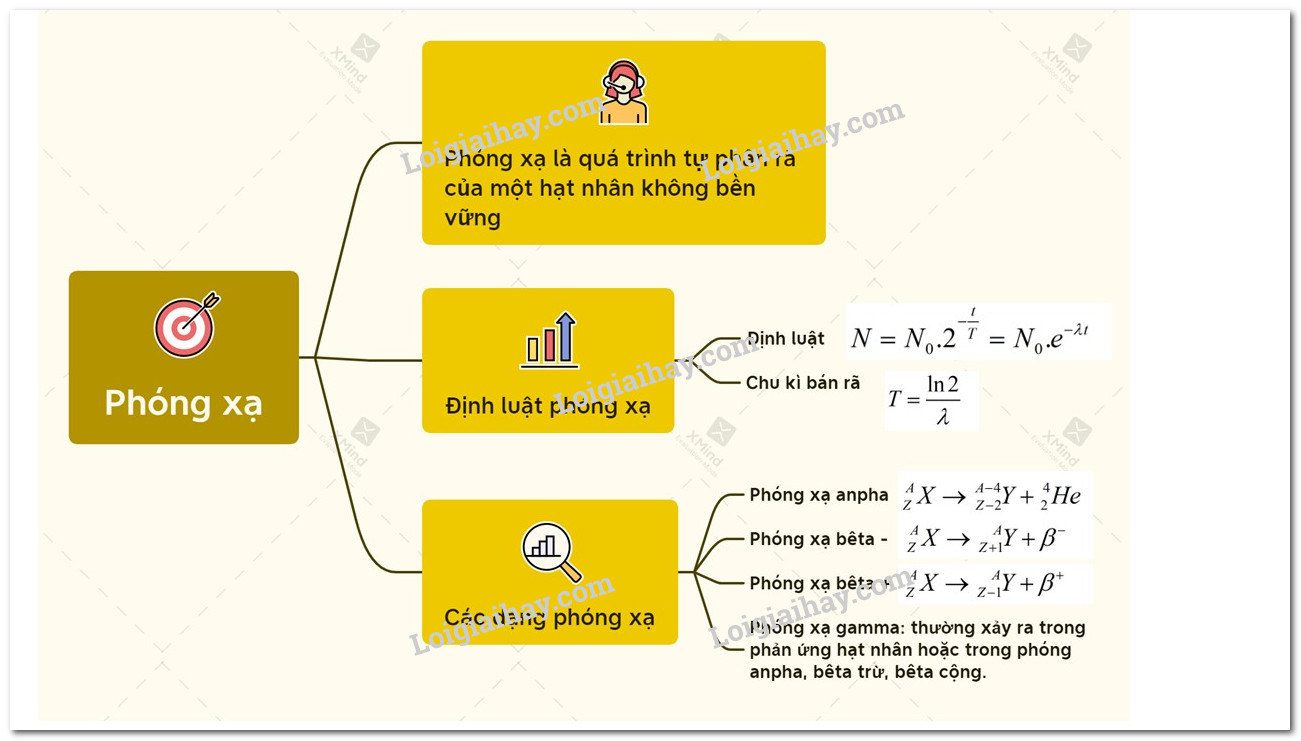
2. Quá trình phân rã và chu kỳ bán rã của chất phóng xạ X
Quá trình phân rã của chất phóng xạ X là một hiện tượng tự nhiên, trong đó các hạt nhân không ổn định của chất phóng xạ này phát ra bức xạ và chuyển đổi thành các hạt nhân ổn định hơn. Khi chất phóng xạ X phân rã, khối lượng của nó sẽ giảm dần theo thời gian.
Chu kỳ bán rã là khái niệm quan trọng trong việc hiểu rõ quá trình phân rã của chất phóng xạ. Chu kỳ bán rã, ký hiệu là \(T\), là khoảng thời gian cần thiết để một nửa số hạt nhân ban đầu của một mẫu chất phóng xạ phân rã. Ví dụ, nếu ban đầu có 20g chất phóng xạ X, thì sau một chu kỳ bán rã, chỉ còn lại 10g chất X.
Ta có công thức tính khối lượng chất phóng xạ còn lại sau thời gian \(t\) như sau:
Trong đó:
- \(m(t)\): Khối lượng chất phóng xạ còn lại sau thời gian \(t\)
- \(m_0\): Khối lượng chất phóng xạ ban đầu
- \(T\): Chu kỳ bán rã của chất phóng xạ
- \(t\): Thời gian kể từ lúc bắt đầu quá trình phân rã
Với công thức trên, bạn có thể dễ dàng tính toán khối lượng chất phóng xạ còn lại sau các chu kỳ bán rã cụ thể, từ đó hiểu rõ hơn về quá trình phân rã của chất phóng xạ X.

3. Phân rã của 20g chất phóng xạ X theo thời gian
Quá trình phân rã của 20g chất phóng xạ X diễn ra theo một quy luật cụ thể, phụ thuộc vào chu kỳ bán rã \(T\). Khi chất phóng xạ này phân rã, lượng chất còn lại giảm dần theo thời gian. Giả sử chu kỳ bán rã của chất X là \(T\), chúng ta có thể tính toán lượng chất còn lại sau một hoặc nhiều chu kỳ bán rã.
Giả sử ban đầu có 20g chất phóng xạ X, khối lượng chất còn lại sau mỗi chu kỳ bán rã có thể được tính như sau:
- Sau 1 chu kỳ bán rã: Khối lượng còn lại là:
- Sau 2 chu kỳ bán rã: Khối lượng còn lại là:
- Sau 3 chu kỳ bán rã: Khối lượng còn lại là:
\[
m_1 = \frac{20}{2} = 10 \, \text{gam}
\]
\[
m_2 = \frac{10}{2} = 5 \, \text{gam}
\]
\[
m_3 = \frac{5}{2} = 2.5 \, \text{gam}
\]
Công thức tổng quát để tính khối lượng chất phóng xạ còn lại sau \(n\) chu kỳ bán rã là:
Trong đó:
- \(m_0\) là khối lượng chất phóng xạ ban đầu (20g).
- \(n\) là số chu kỳ bán rã đã trải qua.
Như vậy, chỉ sau một vài chu kỳ bán rã, khối lượng chất phóng xạ X sẽ giảm đáng kể. Điều này cho thấy tầm quan trọng của việc hiểu rõ quá trình phân rã trong các ứng dụng thực tiễn như xử lý chất thải phóng xạ hay trong các lĩnh vực y học và nghiên cứu khoa học.

4. Các ví dụ và bài tập liên quan
Để hiểu rõ hơn về quá trình phân rã của chất phóng xạ X, chúng ta sẽ cùng xem xét một số ví dụ minh họa và bài tập tính toán khối lượng chất phóng xạ còn lại sau một số chu kỳ bán rã.
4.1 Ví dụ về phân rã chất phóng xạ trong thực tế
Giả sử ban đầu có 20g chất phóng xạ X, với chu kỳ bán rã là 5 năm. Sau 10 năm, khối lượng chất X còn lại là bao nhiêu?
Giải:
Sau 10 năm, chất X đã trải qua:
\[
n = \frac{10}{5} = 2 \, \text{chu kỳ bán rã}
\]
Khối lượng chất X còn lại sau 2 chu kỳ bán rã:
\[
m_2 = \frac{20}{2^2} = 5 \, \text{gam}
\]
Vậy sau 10 năm, khối lượng chất phóng xạ X còn lại là 5g.
4.2 Bài tập tính toán khối lượng chất phóng xạ còn lại
- Ban đầu có 20g chất phóng xạ X, với chu kỳ bán rã là 3 năm. Hãy tính khối lượng còn lại của chất X sau 9 năm.
- Giả sử ban đầu có 40g chất phóng xạ X, sau 15 năm khối lượng còn lại là 5g. Tính chu kỳ bán rã của chất phóng xạ này.
4.3 Các phương pháp giải bài toán liên quan đến chất phóng xạ
Để giải các bài toán liên quan đến phân rã chất phóng xạ, chúng ta cần nắm vững các công thức sau:
- Công thức tính khối lượng còn lại sau \(n\) chu kỳ bán rã:
- Công thức tính số chu kỳ bán rã:
- Công thức tính chu kỳ bán rã khi biết khối lượng ban đầu và khối lượng còn lại:
\[
m_n = \frac{m_0}{2^n}
\]
\[
n = \frac{t}{T}
\]
\[
T = \frac{t}{\log_2 \left(\frac{m_0}{m_t}\right)}
\]
Những công thức này sẽ giúp bạn dễ dàng giải quyết các bài toán liên quan đến phân rã chất phóng xạ, từ đó hiểu sâu hơn về các ứng dụng và ảnh hưởng của chất phóng xạ trong thực tế.